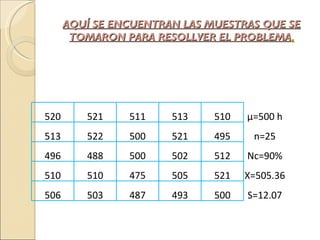
Este documento presenta un problema de distribución binomial. Se muestran 5 muestras de la duración de focos que una persona verifica para conservar un promedio de duración de 50 horas. La conclusión que se debe sacar es si un foco nuevo cuya duración fue de 2 focos entre los valores 0.5 y 0.5 horas satisface este promedio.

1. T - STUDENT
 U fa nte de focos a aque su producto duraáun prom
n brica firm r edio
de 50hora de tra jo. Praconservr este prom estapersona
0 s ba a a edio
verifica2 focos ca m S el vlor yca do ca entre –t
5 da es. i a lcula e
0 5yt 0 5 é se encuentrasa
.0 .0, l tisfecho con estaa a ó ¿ué
firm ci n. Q
conclusió deberáé sa r de unam
n l ca uestrade 2 focos cuy
5 a
dura ó fue?
ci n :

2. AQUÍ SE ENCUENTRAN LAS MUESTRAS QUE SE
TOMARON PARA RESOLLVER EL PROBLEMA.
520 521 511 513 510 µ=500 h
513 522 500 521 495 n=25
496 488 500 502 512 Nc=90%
510 510 475 505 521 X=505.36
506 503 487 493 500 S=12.07

3. SOLUCION
 Para poder resolver el problema lo que se tendrá que hacer será lo
siguiente se aplicara una formula la cual tendremos que desarrollar con los
datos con los que contamos.
 Tendremos que sustituir los datos

t= x -μ
 SI n α = 1- Nc = 10%
 v = n-1 = 24
 t = 2.22

4.  VALOR DE LOS DATOS.. APLICACION DE LA FORMULA
Procedimiento:se demostrara la forma en que se
sustituiran los datos.
 µ=500 h t=505.36-500
t = 2.22
 n=25 12.07 25
 Nc=90% v = 25 -1 = 24
 X=505.36 α = 1- 90% =
10%
 S=12.07

5. Enseguida se muestra la distribución del problema
según el grafico sig.

6. Bernoulli.
 Un ejemplo

7. 1) Al lanzar un dado, ver si se obtiene un 5 (éxito) o cualquier otro valor
(fracaso).
Lo primero que se hace en este experimento es identificar el fracaso o el
éxito, ya que en este de bernoulli solo se pude obtener dos resultados
1)Se considera éxito sacar un 5, a la probabilidad según el teorema de
Laplace (casos favorables dividido entre casos posibles) será 1/5.
p = 1/5
2) Se considera fracaso no sacar un 6, por tanto, se considera fracaso
sacar cualquier otro resultado, entonces a la probabilidad se le restará 1.
q= 1 –p p= 1- 1/5 p=4/5
3) La variable aleatoria X medirá "número de veces que sale un 5", y solo
existen dos valores posibles, 0 (que no salga 5) y 1 (que salga un 5). Por
lo que el parámetro es (X= Be(1/5)
p=1/5

8. La probabilidad de que obtengamos un 5 viene definida como la
probabilidad de que X sea igual a 1. Entonces ahora los datos que
obtuvimos se sustituyen en la fórmula.
P(x=1) = (1/5) 1 * (4/5) 0 = 1/5 = 0.2
La probabilidad de que NO obtengamos un 6 viene definida como la
probabilidad de que X sea igual a 0.
P(x=0) = (1/5)0 * (4/5)1 = 4/5 = 0.8
Este experimento nos dice que hay 0.2 de probabilidad de que salga el
numero 5 en el dado, y de que no salga ese numero existe la probabilidad
del 0.8.

9. Ejemplo binomial
 Se lanza una moneda cuatro veces.
Calcular la probabilidad de que salgan
más caras que cruces.
 B(4, 0.5) p = 0.5q = 0.5

10. explicación
 En el ejemplo anterior se calculan las
probabilidades de que al tirar una moneda
salgan mas caras que cruces y para eso
La moneda es lanzada 4 veces de esos 4
tiros solo 1 cae cara y los otros 3 tiros
cae cruz pero el resultado va a variar
probabilidades:
1cara-3 cruces 2 caras- 2 cruces
3 caras- 1 cruz 2 cruces- 2 caras

11. 5 Ejemplos de Poisson
Si un banco recibe en promedio 6 cheques sin fondo
Ejemplo 1.-
por día, ¿ Cuales son las probabilidades reciba,
b)Cuatro cheque sin fondo en un día dado,
c)B)reciba 10 cheques sin fondo en cualquiera de dos días
consecutivos
Variable discreta= cantidad de personas
Intervalo continuo= una hora
Formula

12.  P(x): Probabilidad de que ocurran x
éxitos
 : Número medio de sucesos esperados
por unidad de tiempo.
 e: es la base de logaritmo natural cuyo
valor es 2.718
 X: es la variable que nos denota el
número de éxitos que se desea que
ocurran

13.  A) x= Variable que nos define el número de
cheques sin fondo que llega al banco en un día
cualquiera;
 El primer paso es extraer los datos
 Tenemos que o el promedio es igual a 6
cheques sin fondo por día
 e= 2.718
 x= 4 por que se pide la probabilidad de que lleguen
cuatro cheques al día

14. Reemplazar valores en las formulas
 =6
 e= 2.718
 X= 4
 P(x=4, = 6) =(6)^4(2.718)^-6
 4!
 =(1296)(0,00248)
 24
 =o,13192
 Es la probabilidad que representa de que lleguen cuatro
cheques sin fondo al día

15.  B)
 X= es la variable que nos define el número de cheques sin fondo que llegan en dos
días consecutivos
 =6x2= 12 Cheques sin fondo en promedio que llegan al banco en dos días
consecutivos
 Lambda por t comprende
 al promedio del cheque a los dos días
 DATOS
 = 12 Cheques sin fondo por día
 e= 2.718
 X=10
 P(x=10, =12 )= (129^10(2.718)^-12
 10!
 =(6,191736*10^10)(0,000006151)
 3628800
 =0,104953 es la es la probalidad de que lleguen 10 cheques sin fondo en dos
días consecutivos