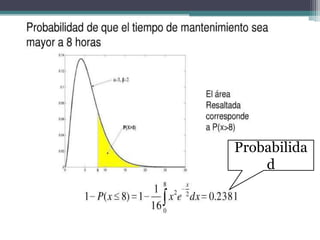
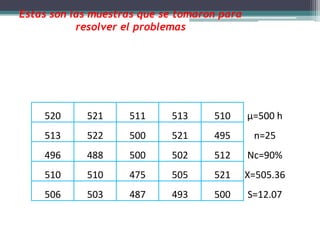
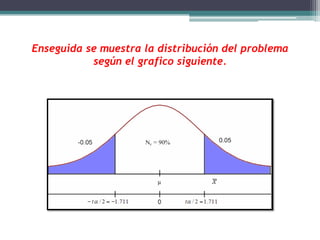
El documento presenta ejemplos de diferentes distribuciones de probabilidad como Bernoulli, binomial, Poisson, normal y gamma. Incluye un ejemplo de una variable aleatoria normal donde se analiza si la duración promedio de 25 focos cumple con las afirmaciones del fabricante.

1. Ejemplos explicados de bernoulli, binomial,
poisson, normal, gamma, t de student
Christian Michel Álvarez Ramírez.

2. 1) Al lanzar un dado, ver si se obtiene un 5 (éxito) o cualquier otro valor (fracaso).
Lo primero que se hace en este experimento es identificar el fracaso o el éxito, ya
que en este de bernoulli solo se pude obtener dos resultados
1)Se considera éxito sacar un 5, a la probabilidad según el teorema de
Laplace (casos favorables dividido entre casos posibles) será 1/5.
p = 1/5
2) Se considera fracaso no sacar un 6, por tanto, se considera fracaso sacar
cualquier otro resultado, entonces a la probabilidad se le restará 1.
q= 1 –p p= 1- 1/5 p=4/5
3) La variable aleatoria X medirá "número de veces que sale un 5", y solo existen
dos valores posibles, 0 (que no salga 5) y 1 (que salga un 5). Por lo que el
parámetro es (X= Be(1/5)
p=1/5

3. La probabilidad de que obtengamos un 5 viene definida como la
probabilidad de que X sea igual a 1. Entonces ahora los datos que
obtuvimos se sustituyen en la fórmula.
P(x=1) = (1/5) 1 * (4/5) 0 = 1/5 = 0.2
La probabilidad de que NO obtengamos un 6 viene definida como la
probabilidad de que X sea igual a 0.
P(x=0) = (1/5)0 * (4/5)1 = 4/5 = 0.8
Este experimento nos dice que hay 0.2 de probabilidad de que salga el
numero 5 en el dado, y de que no salga ese numero existe la
probabilidad del 0.8.

4. Ejemplo binomial
• Se lanza una moneda cuatro veces. Calcular la
probabilidad de que salgan más caras que
cruces.
• B(4, 0.5) p = 0.5q = 0.5

5. explicación
• En el ejemplo anterior se calculan las
probabilidades de que al tirar una moneda
salgan mas caras que cruces y para eso
La moneda es lanzada 4 veces de esos 4 tiros
solo 1 cae cara y los otros 3 tiros cae cruz pero el
resultado va a variar
probabilidades:
1cara-3 cruces 2 caras- 2 cruces
3 caras- 1 cruz 2 cruces- 2 caras

6. Ejemplos de Poisson
Si un banco recibe en promedio 6 cheques sin fondo
Ejemplo 1.-
por día, ¿ Cuales son las probabilidades reciba,
a)Cuatro cheque sin fondo en un día dado,
b)B)reciba 10 cheques sin fondo en cualquiera de dos días
consecutivos
Variable discreta= cantidad de personas
Intervalo continuo= una hora
Formula

7. • P(x): Probabilidad de que ocurran x éxitos
• : Número medio de sucesos esperados por
unidad de tiempo.
• e: es la base de logaritmo natural cuyo valor es
2.718
• X: es la variable que nos denota el número de
éxitos que se desea que ocurran

8. • A) x= Variable que nos define el número de cheques
sin fondo que llega al banco en un día cualquiera;
• El primer paso es extraer los datos
• Tenemos que o el promedio es igual a 6 cheques
sin fondo por día
• e= 2.718
• x= 4 por que se pide la probabilidad de que lleguen
cuatro cheques al día

9. Reemplazar valores en las formulas
• =6
• e= 2.718
• X= 4
• P(x=4, = 6) =(6)^4(2.718)^-6
• 4!
• =(1296)(0,00248)
• 24
• =o,13192
• Es la probabilidad que representa de que lleguen cuatro
cheques sin fondo al día

10. • B)
• X= es la variable que nos define el número de cheques sin fondo que llegan en dos
días consecutivos
• =6x2= 12 Cheques sin fondo en promedio que llegan al banco en dos días
consecutivos
• Lambda por t comprende
• al promedio del cheque a los dos días
• DATOS
• = 12 Cheques sin fondo por día
• e= 2.718
• X=10
• P(x=10, =12 )= (129^10(2.718)^-12
• 10!
• =(6,191736*10^10)(0,000006151)
• 3628800
• =0,104953 es la es la probalidad de que lleguen 10 cheques sin fondo en dos
días consecutivos

11. Explicación del
problema

12. Una variable aleatoria continua, X, sigue una distribución
normal de media μ y desviación típica σ, y se designa
por N(μ, σ), si se cumplen las siguientes condiciones:
1. La variable puede tomar cualquier valor: (-∞, +∞)
2. La función de densidad, es la expresión en términos de
ecuación matemática de la curva de Gauss:

13. • Curva de la distribución normal
• El campo de existencia es cualquier valor real, es decir, (-
∞, +∞).
• Es simétrica respecto a la media µ.
• Tiene un máximo en la media µ.
• Crece hasta la media µ y decrece a partir de ella.
• En los puntos µ − σ y µ + σ presenta puntos de inflexión.
• El eje de abscisas es una asíntota de la curva.

14. El área del recinto determinado por la función y el eje
de abscisas es igual a la unidad.
Al ser simétrica respecto al eje que pasa por x =
µ, deja un área igual a 0.5 a la izquierda y otra
igual a 0.5 a la derecha.
La probabilidad equivale al área encerrada bajo
la curva.
p(μ - σ < X ≤ μ + σ) = 0.6826 = 68.26 %
p(μ - 2σ < X ≤ μ + 2σ) = 0.954 = 95.4 %
p(μ - 3σ < X ≤ μ + 3σ) = 0.997 = 99.7 %

15. Distribución
Gamma

16. Parámetros
A continuación se sustituye la formula
en base alas 8 horas.

17. Formula

18. Probabilida
d

19. Explicación del ejemplo
 Un fabricante de focos afirma que su producto durará un
promedio de 500 horas de trabajo. Para conservar este
promedio esta persona verifica 25 focos cada mes. Si el valor y
calculado cae entre –t 0.05 y t 0.05, él se encuentra satisfecho
con esta afirmación. ¿Qué conclusión deberá él sacar de una
muestra de 25 focos cuya duración fue?:

20. Estas son las muestras que se tomaron para
resolver el problemas
520 521 511 513 510 µ=500 h
513 522 500 521 495 n=25
496 488 500 502 512 Nc=90%
510 510 475 505 521 X=505.36
506 503 487 493 500 S=12.07

21. Solución
 Para poder resolver el problema lo que se tendrá que hacer será lo siguiente
se aplicara una formula la cual tendremos que desarrollar con los datos con
los que contamos.
 Tendremos que sustituir los datos
 t= x -μ
 SI n α = 1- Nc = 10%
 v = n-1 = 24
 t = 2.22

22.  VALOR DE LOS DATOS.. APLICACION DE LA FORMULA
Procedimiento:se demostrara la forma en que se
sustituiran los datos.
 µ=500 h t=505.36-500 t=
2.22
 n=25 12.07 25
 Nc=90% v = 25 -1 = 24
 X=505.36 α = 1- 90% = 10%
 S=12.07

23. Enseguida se muestra la distribución del problema
según el grafico siguiente.