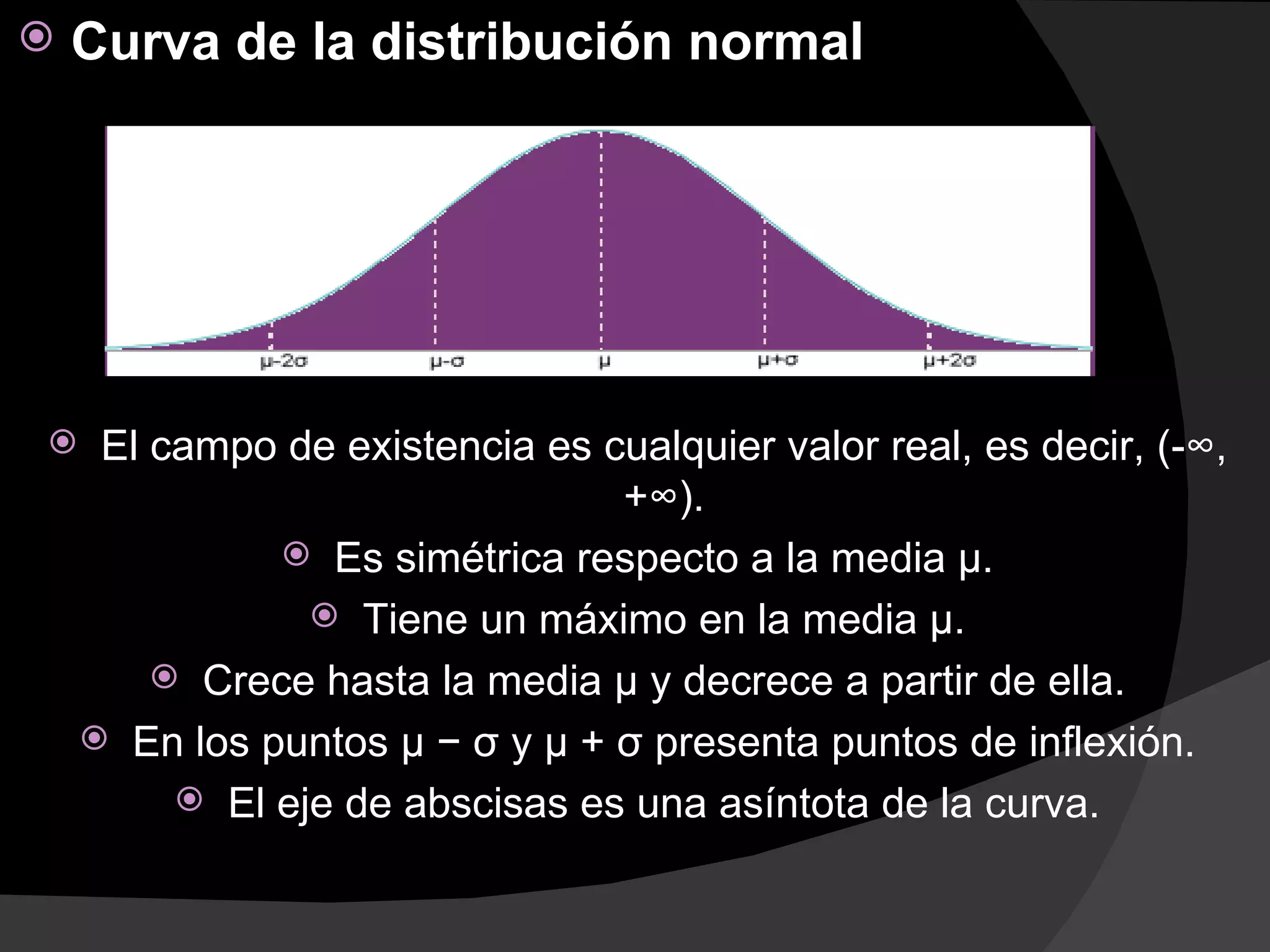
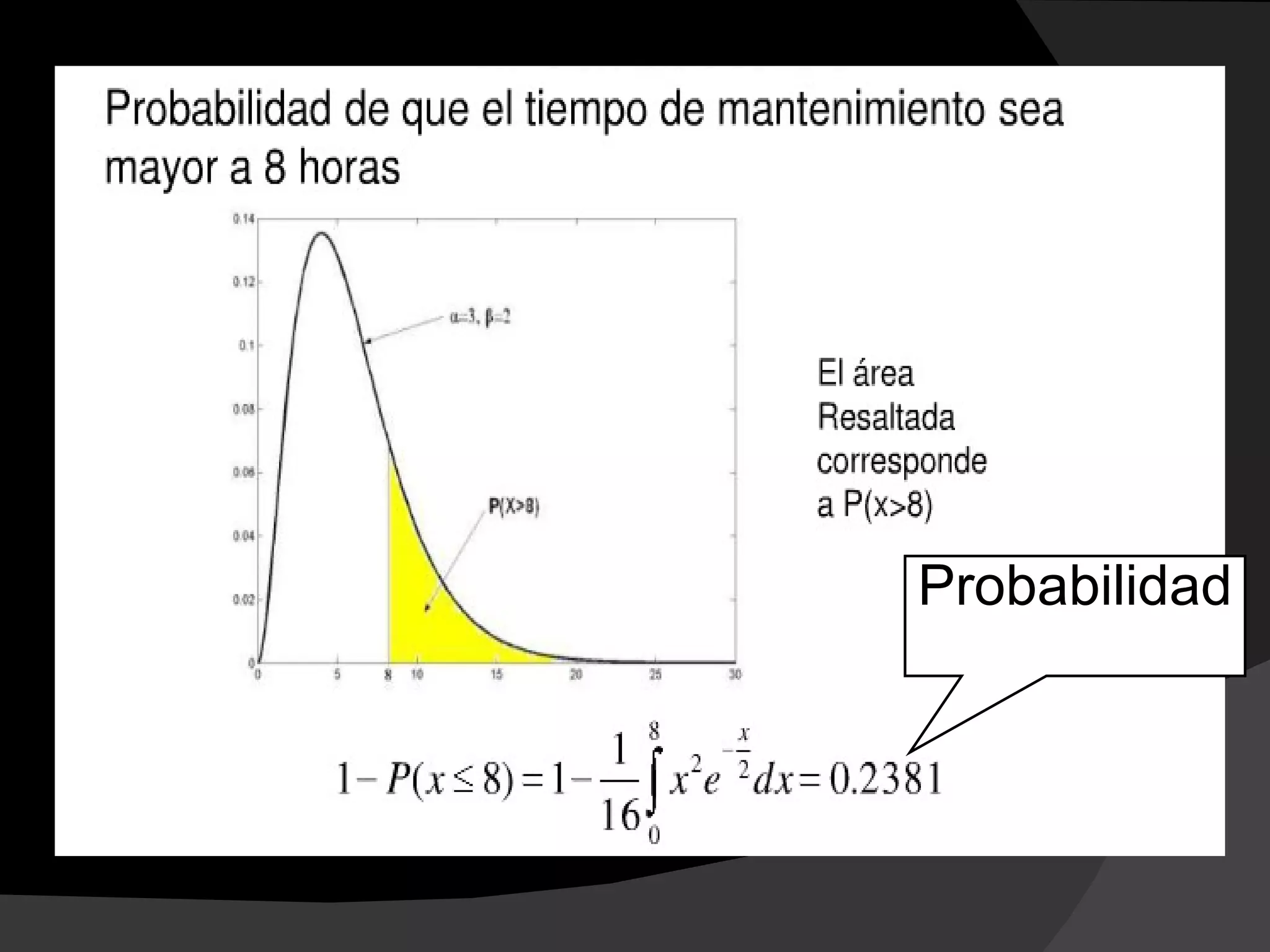
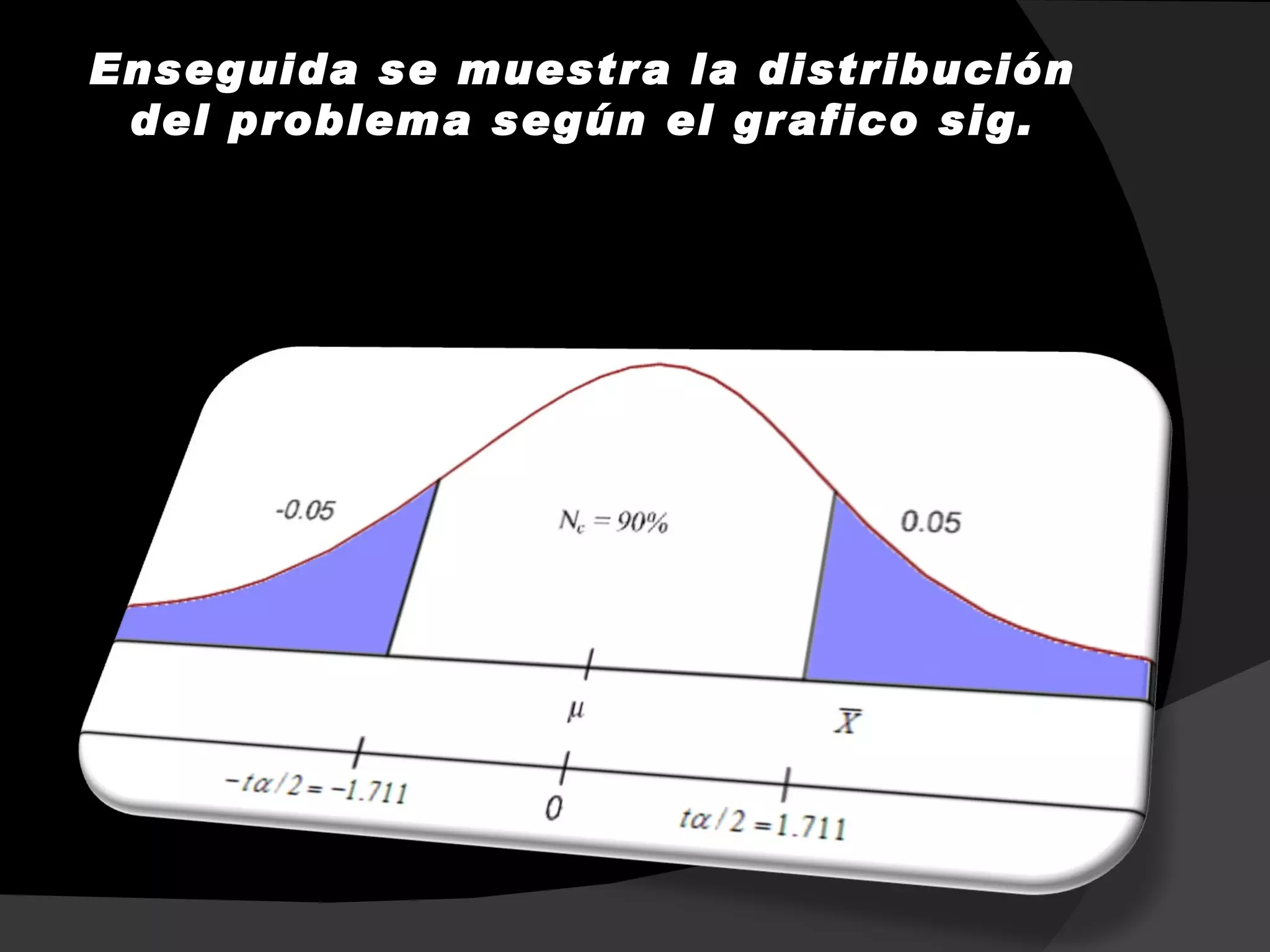
Este documento presenta ejemplos de diferentes distribuciones de probabilidad, incluyendo la distribución de Bernoulli, la binomial, la normal y la t de Student. Explica cómo calcular la probabilidad de eventos en cada distribución utilizando fórmulas como la de probabilidad de Bernoulli, la binomial, la normal y la t de Student. También proporciona un ejemplo numérico para ilustrar cómo aplicar cada fórmula.

1. Universidad Tecnológica
de Torreón.
Ejemplos de las diferentes distribuciones
de probabilidad.
Lizbeth Martínez
2A

2. 1) Al lanzar un dado, ver si se obtiene un 5 (éxito) o
cualquier otro valor (fracaso).
Lo primero que se hace en este experimento es
identificar el fracaso o el éxito, ya que en este de
bernoulli solo se pude obtener dos resultados
1)Se considera éxito sacar un 5, a la probabilidad
según el teorema de Laplace (casos favorables
dividido entre casos posibles) será 1/5.
p = 1/5
2) Se considera fracaso no sacar un 6, por tanto, se
considera fracaso sacar cualquier otro resultado,
entonces a la probabilidad se le restará 1.
q= 1 –p p= 1- 1/5
p=4/5
3) La variable aleatoria X medirá "número de veces
que sale un 5", y solo existen dos valores posibles, 0
(que no salga 5) y 1 (que salga un 5). Por lo que el
parámetro es (X= Be(1/5)

3. La pr obabilidad de que obtengamos un 5 viene definida como
la pr obabilidad de que X sea igual a 1. Entonces ahor a los
datos que obtuvimos se sustituyen en la fór mula.
P(x=1) = (1/5) 1 * (4/5) 0 = 1/5 = 0.2
La pr obabilidad de que NO obtengamos un 6 viene definida
como la pr obabilidad de que X sea igual a 0.
P(x=0) = (1/5) 0 * (4/5) 1 = 4/5 = 0.8
Este experimento nos dice que hay 0.2 de pr obabilidad de
que salga el numer o 5 en el dado, y de que no salga ese
numer o existe la pr obabilidad del 0.8.

4. EJEMPLO BINOMIAL.

6. Ejemplo 1.-Si un banco recibe en promedio 6 cheques sin fondo
por día, ¿ Cuales son las probabilidades reciba,
b)Cuatro cheque sin fondo en un día dado,
c)B)reciba 10 cheques sin fondo en cualquiera de dos días
consecutivos
Variable discreta= cantidad de personas
Intervalo continuo= una hora
Formula

7.  P(x): Probabilidad de que ocurran x éxitos
 : Número medio de sucesos esperados
por unidad de tiempo.
 e: es la base de logaritmo natural cuyo valor
es 2.718
 X: es la variable que nos denota el número
de éxitos que se desea que ocurran

8.  A) x= Variable que nos define el número de
cheques sin fondo que llega al banco en un día
cualquiera;
 El primer paso es extraer los datos
 Tenemos que o el promedio es igual a 6
cheques sin fondo por día
 e= 2.718
 x= 4 por que se pide la probabilidad de que
lleguen cuatro cheques al día

9. Reemplazar valores en las formulas
 =6
 e= 2.718
 X= 4
 P(x=4, = 6) =(6)^4(2.718)^-6
 4!
 =(1296)(0,00248)
 24
 =o,13192
 Es la probabilidad que representa de que lleguen cuatro
cheques sin fondo al día

10.  B)
 X= es la variable que nos define el número de cheques sin fondo que llegan en dos
días consecutivos
 =6x2= 12 Cheques sin fondo en promedio que llegan al banco en dos días
consecutivos
 Lambda por t comprende
 al promedio del cheque a los dos días
 DATOS
 = 12 Cheques sin fondo por día
 e= 2.718
 X=10
 P(x=10, =12 )= (129^10(2.718)^-12
 10!
 =(6,191736*10^10)(0,000006151)
 3628800
 =0,104953 es la es la probalidad de que lleguen 10 cheques sin fondo en dos
días consecutivos

11. EJEMPLO DE NORMAL:
Una variable aleatoria continua, X, sigue
una distribución normal de media μ y desviación
típica σ, y se designa por N(μ , σ ), si se cumplen las
siguientes condiciones:
1. La variable puede tomar cualquier valor: (-∞, +∞)
2. La función de densidad, es la expresión en términos
de ecuación matemática de la curva de Gauss:

12.  Curva de la distribución normal
 El campo de existencia es cualquier valor real, es decir, (-∞,
+∞).
 Es simétrica respecto a la media µ.
 Tiene un máximo en la media µ.
 Crece hasta la media µ y decrece a partir de ella.
 En los puntos µ − σ y µ + σ presenta puntos de inflexión.
 El eje de abscisas es una asíntota de la curva.

13. El área del recinto determinado por la función y el eje
de abscisas es igual a la unidad.
Al ser simétrica respecto al eje que pasa por x = µ,
deja un área igual a 0.5 a la izquierda y otra igual a
0.5 a la derecha.
La probabilidad equivale al área encerrada bajo la
curva.
p(μ - σ < X ≤ μ + σ) = 0.6826 = 68.26 %
p(μ - 2σ < X ≤ μ + 2σ) = 0.954 = 95.4 %
p(μ - 3σ < X ≤ μ + 3σ) = 0.997 = 99.7 %

15. Formula

16. Probabilidad

17. EJEMPLO DE T DE STUDENT:
Un fabricante de focos afirma que su
producto durará un promedio de 500
horas de trabajo. Para conservar este
promedio esta persona verifica 25
focos cada mes. Si el valor y
calculado cae entre –t 0.05 y t 0.05,
él se encuentra satisfecho con esta
afirmación. ¿Qué conclusión deberá él
sacar de una muestra de 25 focos
cuya duración fue?:

18. AQUÍ SE ENCUENTRAN LAS MUESTRAS QUE
SE TOMARON PARA RESOLLVER EL
PROBLEMA.
520 521 511 513 510 µ=500 h
513 522 500 521 495 n=25
496 488 500 502 512 Nc=90%
510 510 475 505 521 X=505.36
506 503 487 493 500 S=12.07

19. SOLUCION
 Para poder resolver el problema lo que se tendrá que hacer será lo
siguiente se aplicara una formula la cual tendremos que desarrollar
con los datos con los que contamos.
 Tendremos que sustituir los datos

t= x -μ
 SI n α = 1- Nc = 10%
 v = n-1 = 24
 t = 2.22

20. Procedimiento:se demostrara la forma en que
se sustituiran los datos.
 VALOR DE LOS DATOS.. APLICACION DE LA
FORMULA
 µ=500 h t=505.36-500 t=
2.22
 n=25 12.07 25
 Nc=90% v = 25 -1 = 24
 X=505.36 α = 1- 90% = 10%

21. Enseguida se muestra la distribución
del problema según el grafico sig.