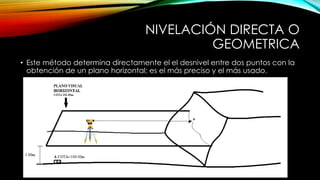
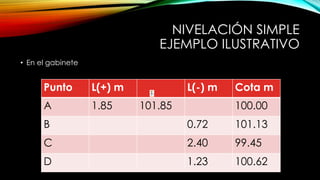
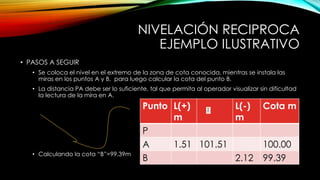
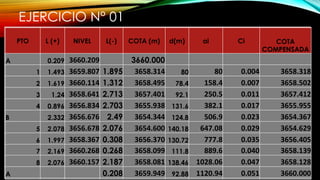
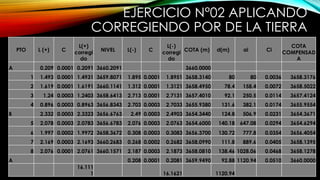
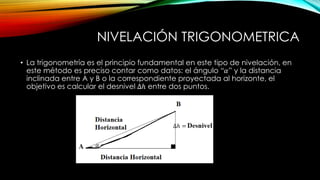
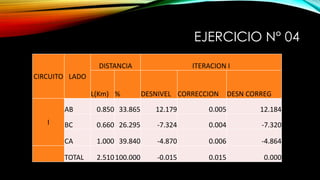
El documento se centra en la altimetría y sus métodos, explicando conceptos clave como nivelación, cotas, y referencia de altura. Se describen diferentes tipos de nivelación, como la directa o geométrica, la reciproca y la compuesta, así como su aplicación y precisión. Además, se ofrecen ejemplos prácticos y se enfatiza la importancia de la precisión en las mediciones realizadas en el campo.

1. ALTIMETRIA
Docente: Ing. Saúl Huamán Quispe

2. SEGUNDA UNIDAD: ALTIMETRÍA
• Altimetría
• Nivelación
• Métodos e instrumentos
• Itinerarios de nivelación
• Precisión, errores y correcciones
• Pendientes y buzamientos
• Perfiles longitudinales y transversales

3. ALTIMETRIA
• La altimetría considera las diferencias de nivel existentes entre puntos de un terreno
o construcción. Para poder conocer estas diferencias de nivel hay que medir
distancias verticales directa o indirectamente. Esta operación se denomina
NiVELACIÓN.
• Las distancias verticales, que se miden a partir de una superficie de nivel p plano de
referencia arbitrario, que debe ser normal a la dirección de la plomada, se
denomina Cotas. Cuando el plano de referencia coincide con el nivel del mar, las
distancias verticales medidas a partir de dicho plano se denomina Altitud o Alturas
• La superficie de nivel que se toma como referencia, bien sea real o imaginaria, se
llama DATUM.
• BM (Bench Mark); se denomina así a un punto de carácter más o menos
permanente, del cual se conocen se localización y su elevación. Su cota, que ha
sido determinada previamente por una nivelación de precisión o adoptada
arbitrariamente, sirve de base para efectuar la nivelación, también se le llama cota
absoluta.

5. NIVELACIÓN
• Es el proceso mediante el cual se determina la altitud de un punto respecto
a un plano horizontal de referencia.
• Plano horizontal; es aquel plano perpendicular a la dirección de la vertical y
tangente a una superficie de nivel en un solo punto.
• Superficie de nivel; es la superficie perpendicular a la dirección de la
vertical.
• Nivel medio del mar; es el nivel ±0.00 adoptado convencionalmente y viene
a ser el promedio de la máxima elevación del mar (PLEAMAR) y su máximo
descenso (BAJAMAR) en un lugar.

6. CLASES DE NIVELACIÓN
• Nivelación directa o geométrica
• Nivelación indirecta
• Nivelación trigonométrica
• Nivelación barométrica
¿ como se nivela un B.M.?

7. NIVELACIÓN DIRECTA O
GEOMETRICA
• Este método determina directamente el el desnivel entre dos puntos con la
obtención de un plano horizontal; es el más preciso y el más usado.

8. CASOS GENERALES EN UNA
NIVELACIÓN GEOMETRICA
a) Nivelación relativa;
Cuando solo sea necesario conocer el desnivel entre los puntos de la zona de
trabajo.
Para ello se asume una cota arbitraria a uno de los puntos lo suficientemente grande
para no tener en el curso de la nivelación cotas negativas, o bien el punto más bajo
se le da una cota de cero.
b) Nivelación absoluta;
Cuando se preciso trabajar con cotas absolutas, en este caso se ubica el B.M.
De un punto cercano a la zona de trabajo; en el Perú el Instituto Geográfico Nacional
nos puede proporcionar dicho punto. A continuación se lleva a cabo una nivelación
de circuito cerrado entre B.M. y el punto más cercano a la zona por nivelar.
Por ultimo se realiza la nivelación en la zona establecida

9. ELEMENTOS IMPORTANTES DE UNA
NIVELACIÓN GEOMÉTRICA
• Puntos de nivel primario (Bancos de nivel).- Son puntos de contro, estas
deben ser monumentadas
• Puntos de nivel secundario (Puntos de cambio).- Son puntos de apoyo, en
donde se coloca las miras para para efectuar las lecturas correspndientes.
• Vista atrás L(+).- Lectura hacia el punto conocido.
• Vista adelante L(-).- Lectura hacia el punto por conocer.

10. TIPOS DE NIVELACIÓN
GEOMÉTRICA
• NIVELACIÓN SIMPLE
• NIVELACIÓN RECIPROCA
• NIVELACIÓN COMPUESTA

11. NIVELACIÓN SIMPLE
• Sirve para conocer de uno o más puntos de terreno por medio de una sola
estación instrumental.
• PASOS A SEGUIR
• Se coloca la mira en el punto de cota conocido (A)
• Se ubica el punto de cota por conocer (B)
• Se instala el nivel en un punto equidistante a los antes mencionados.
• La distancia nivel – no debe sobrepasar de 120metros, sin embargo es
recomendable trabajar con una distancia máxima de 50 metros.

12. NIVELACIÓN SIMPLE
• Con ayuda del nivel se visa la mira en el punto de cota conocida anota en
la libreta
• Se coloca la mira en el punto de cota por conocer.
• Con ayuda del nivel, se visa la mira en el punto de cota por conocer =L(-) y
se anota en la libreta de campo.

13. NIVELACIÓN SIMPLE
EJEMPLO ILUSTRATIVO
• Dado el punto “A” de cota +100.00m se desea conocer las cotas de los
puntos B, C y D.
• En el campo.
Punto L(+) m L(-) m Cota m
A 1.85 100.00
B 0.72
C 2.40
D 1.23

14. NIVELACIÓN SIMPLE
EJEMPLO ILUSTRATIVO
• En el gabinete
Punto L(+) m L(-) m Cota m
A 1.85 101.85 100.00
B 0.72 101.13
C 2.40 99.45
D 1.23 100.62

15. NIVELACIÓN RECIPROCA
•Esta nivelación se utiliza cuando
•Se desea comprobar si el eje óptico del
anteojo es paralelo a la dirección de nivel
tubular
•No es posible colocar el nivel entre dos
puntos de mira, ya sea porque se interpone
un río, un pantano u otro obstáculo.

16. NIVELACIÓN RECIPROCA
EJEMPLO ILUSTRATIVO
• PASOS A SEGUIR
• Se coloca el nivel en el extremo de la zona de cota conocida, mientras se instala las
miras en los puntos A y B, para luego calcular la cota del punto B.
• La distancia PA debe ser lo suficiente, tal que permita al operador visualizar sin dificultad
la lectura de la mira en A.
• Calculando la cota “B”=99.39m
Punto L(+)
m
L(-)
m
Cota m
P
A 1.51 101.51 100.00
B 2.12 99.39

17. NIVELACIÓN RECIPROCA
EJEMPLO ILUSTRATIVO
• Se traslada el nivel a un punto Q, tal que aproximadamente PA=QB, para
luego calcular nuevamente la cota en B
• Calculando cota “B”=99.41m
Punto L(+)
m
L(-) m Cota m
Q
A 0.64 100.64 100.00
B 1.23 99.41

18. NIVELACIÓN COMPUESTA
• Es una sucesión de niveles simples relacionados entre si, se utiliza cuando se
requiere la diferencia de nivel entre dos puntos muy distanciados o cuando
la visibilidad de una estación no le permite.

19. NIVELACIÓN COMPUESTA
EJEMPLO ILUSTRATIVO
• A continuación mostramos
un ejercicio de dos puntos
lejanos, en los cuales, “A”
tiene como cota +100.00m
el problema consiste en
determinar la cota de “B”.
• Por la falta de visibilidad
utilizaremos la nivelación
compuesta
B
A

20. NIVELACIÓN COMPUESTA
EJEMPLO ILUSTRATIVO
Punto L(+)
m
L(-)
m
Cota
m
A 2.54 102,54 100.00
1 1.42 101.12
A
1

21. NIVELACIÓN COMPUESTA
EJEMPLO ILUSTRATIVO
Punto L(+)
m
L(-) m Cota m
1 0.56 101.68 101.12
2 2.53 99.15
2
1

22. NIVELACIÓN COMPUESTA
EJEMPLO ILUSTRATIVO
Punto L(+)
m
L(-)
m
Cota
m
2 1.44 100.59 99.15
3 0.54 100.05
3
2

23. NIVELACIÓN COMPUESTA
EJEMPLO ILUSTRATIVO
Punto L(+)
m
L(-) m Cota
m
3 2.56 102.61 100.05
B 1.82 100.79
B
3

24. B
3
2
A
1

25. NIVELACIÓN COMPUESTA
EJEMPLO ILUSTRATIVO
Punto L(+) m L(-) m Cota m
A 2.54 100.00
1 0.56 1.42
2 1.44 2.53
3 2.56 0.54
B 1.82
EN CAMPO
Punto L(+) m L(-) m Cota m
A 2.54 102.54 100.00
1 0.56 101.68 1.42 101.12
2 1.44 100.59 2.53 99.15
3 2.56 102.61 0.54 100.05
B 1.82 100.79
EN GABINETE

26. COMPROBACIÓN DEL CALCULO
MATEMÁTICO DE LA LIBRETA
• 𝐿(+) − 𝐿 − = 𝐶𝑜𝑡𝑎 𝑓𝑖𝑛𝑎𝑙 − 𝐶𝑜𝑡𝑎 𝑖𝑛𝑖𝑐𝑖𝑎𝑙
• 𝐿 + = 7.10
• 𝐿 − = 6.31
• 𝐶𝑜𝑡𝑎 𝑓𝑖𝑛𝑎𝑙 = 100.79𝑚
• 𝐶𝑜𝑡𝑎 𝑖𝑛𝑖𝑐𝑖𝑎𝑙 = 100.00𝑚
• 𝐸𝑐 = 𝐿(+) − 𝐿 − = 𝐶𝑜𝑡𝑎 𝑓𝑖𝑛𝑎𝑙 − 𝐶𝑜𝑡𝑎 𝑖𝑛𝑖𝑐𝑖𝑎𝑙

27. PRECISIÓN EN UNA NIVELACIÓN
COMPUESTA
• La precisión en una nivelación está en relación directa al objeto que se persigue;
así pues si se requiere realizar un levantamiento preliminar, no justificara usara un
equipo de alta precisión por cuanto ello llevaría una mayor inversión económica.
• No obstante cualquiera sea el caso, es necesario tomar ciertas precauciones
cotidianas como:
• Revisar y ajustar el instrumento antes de ser usado.
• No apoyarse en el trípode o nivel.
• No instalar el equipo en zonas de posible vibración (como en las calzadas
vehiculares).
• Tratar de nivelar en climas templados, dado que una alta o baja temperatura dilata
o contrae respectivamente la mira además de afectar al equipo.
• Evitar trabajar en épocas de viento y/o lluvia.

28. PRECISIÓN EN UNA NIVELACIÓN
COMPUESTA
• Sin embargo, por más precaución que se tenga, es imposible evitar la presencia de
errores accidentales. Es posible cuantificar la precisión mediante el error máximo
tolerable, el valor de dicho error está en función de dos parámetros.
• El error kilométrico (e).- Máximo error accidental del instrumento en un itinerario de 1
kilómetro.
• Número de Kilómetros (k).- La distancia en kilómetros del itinerario.
•
• 𝐸 𝑚𝑎𝑥 = 𝑒 𝑘
• 𝐸 𝑚𝑎𝑥 = 𝐸𝑟𝑟𝑜𝑟 𝑚𝑎𝑥𝑖𝑚𝑜 𝑡𝑜𝑙𝑒𝑟𝑎𝑏𝑙𝑒 (𝑚𝑒𝑡𝑟𝑜𝑠)
• 𝑒 = 𝐸𝑟𝑟𝑜𝑟 𝑘𝑖𝑙𝑜𝑚𝑒𝑡𝑟𝑖𝑐𝑜 (𝑚𝑒𝑡𝑟𝑜𝑠)
• 𝑘 = 𝑁ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑘𝑖𝑙𝑜𝑚𝑒𝑡𝑟𝑜𝑠

29. PRECISIÓN EN UNA NIVELACIÓN
COMPUESTA
• Nivelación Aproximada: Visuales hasta 300m, con una aproximación de hasta 5cm
• 𝐸 𝑚𝑎𝑥 = ±0.10 𝑘
• Nivelación Ordinaria: Visuales hasta 150m, con una aproximación de hasta 0.5cm
• 𝐸 𝑚𝑎𝑥 = ±0.02 𝑘
• Nivelación Precisa: Visuales hasta 100m, con una precisión de hasta 0.1cm
• 𝐸 𝑚𝑎𝑥 = ±0.01 𝑘
• Nivelación de alta precisión: Visuales hasta 100m, con una precisión de hasta 0.1cm, para medir las distancias
se mide por el método de la estadia.
• 𝐸 𝑚𝑎𝑥 = ±0.004 𝑘
• La siguiente tabla muestra los datos de una nivelación cerrada; si se requiere una nivelación ordinaria, se puede
realizar las compensaciones de cotas.
• Error máximo accidental
• 𝑬 𝒎𝒂𝒙 = ±𝟎. 𝟏𝟎 𝒌

30. EJERCICIO N° 01
PTO L (+) NIVEL L(-) COTA (m) d(m)
A 0.209 3660.000
1 1.493 1.895 80
2 1.619 1.312 78.4
3 1.24 2.713 92.1
4 0.896 2.703 131.6
B 2.332 2.49 124.8
5 2.078 2.076 140.18
6 1.997 0.308 130.72
7 2.169 0.268 111.8
8 2.076 2.187 138.46
A 0.208 92.88
𝑪𝒊 = −
𝜺 𝒄×𝒂 𝒊
𝒅𝒕
PTO L (+) NIVEL L(-) COTA (m) d(m)
A 0.209 3660.209 3660.000
1 1.493 3659.807 1.895 3658.314 80
2 1.619 3660.114 1.312 3658.495 78.4
3 1.24 3658.641 2.713 3657.401 92.1
4 0.896 3656.834 2.703 3655.938 131.6
B 2.332 3656.676 2.49 3654.344 124.8
5 2.078 3656.678 2.076 3654.600 140.18
6 1.997 3658.367 0.308 3656.370 130.72
7 2.169 3660.268 0.268 3658.099 111.8
8 2.076 3660.157 2.187 3658.081 138.46
A 0.208 3659.949 92.88

31. EJERCICIO N° 01
PTO L (+) NIVEL L(-) COTA (m) d(m) ai Ci COTA
COMPENSADA
A 0.209 3660.209 3660.000
1 1.493 3659.807 1.895 3658.314 80
2 1.619 3660.114 1.312 3658.495 78.4
3 1.24 3658.641 2.713 3657.401 92.1
4 0.896 3656.834 2.703 3655.938 131.6
B 2.332 3656.676 2.49 3654.344 124.8
5 2.078 3656.678 2.076 3654.600 140.18
6 1.997 3658.367 0.308 3656.370 130.72
7 2.169 3660.268 0.268 3658.099 111.8
8 2.076 3660.157 2.187 3658.081 138.46
A 0.208 3659.949 92.88
PTO L (+) NIVEL L(-) COTA (m) d(m) ai Ci COTA
COMPENSADA
A 0.209 3660.209 3660.000
1 1.493 3659.807 1.895 3658.314 80 80
2 1.619 3660.114 1.312 3658.495 78.4 158.4
3 1.24 3658.641 2.713 3657.401 92.1 250.5
4 0.896 3656.834 2.703 3655.938 131.6 382.1
B 2.332 3656.676 2.49 3654.344 124.8 506.9
5 2.078 3656.678 2.076 3654.600 140.18 647.08
6 1.997 3658.367 0.308 3656.370 130.72 777.8
7 2.169 3660.268 0.268 3658.099 111.8 889.6
8 2.076 3660.157 2.187 3658.081 138.46 1028.06
A 0.208 3659.949 92.88 1120.94
PTO L (+) NIVEL L(-) COTA (m) d(m) ai Ci COTA
COMPENSADA
A 0.209 3660.209 3660.000
1 1.493 3659.807 1.895 3658.314 80 80 0.004 3658.318
2 1.619 3660.114 1.312 3658.495 78.4 158.4 0.007 3658.502
3 1.24 3658.641 2.713 3657.401 92.1 250.5 0.011 3657.412
4 0.896 3656.834 2.703 3655.938 131.6 382.1 0.017 3655.955
B 2.332 3656.676 2.49 3654.344 124.8 506.9 0.023 3654.367
5 2.078 3656.678 2.076 3654.600 140.18 647.08 0.029 3654.629
6 1.997 3658.367 0.308 3656.370 130.72 777.8 0.035 3656.405
7 2.169 3660.268 0.268 3658.099 111.8 889.6 0.040 3658.139
8 2.076 3660.157 2.187 3658.081 138.46 1028.06 0.047 3658.128
A 0.208 3659.949 92.88 1120.94 0.051 3660.000

32. CORREGIENDO POR DE LA TIERRA
𝐶 =
6
14
(
𝐷2
𝑅
)𝐶 = 𝐸 𝐶 + 𝐸 𝑅
𝐸 𝐶 =
𝐷2
2𝑅
𝐸 𝑅 = −
𝐷2
14𝑅
𝐸𝑟𝑟𝑜𝑟 𝑝𝑜𝑟 𝑐𝑢𝑟𝑣𝑎𝑡𝑢𝑟𝑎 𝑑𝑒 𝑙𝑎 𝑡𝑖𝑒𝑟𝑟𝑎
𝐸𝑟𝑟𝑜𝑟 𝑝𝑜𝑟 𝑟𝑒𝑓𝑟𝑎𝑐𝑐𝑡𝑖ó𝑛 𝑑𝑒 𝑙𝑎 𝑡𝑖𝑒𝑟𝑟𝑎

33. EJERCICIO N°02 APLICANDO
CORREGIENDO POR DE LA TIERRA
PTO L (+) C
L(+)
corregi
do
NIVEL L(-) C
L(-)
corregi
do
COTA (m) d(m) ai Ci
COTA
COMPENSAD
A
A 0.209 3660.0000
1 1.493 1.895 80
2 1.619 1.312 78.4
3 1.24 2.713 92.1
4 0.896 2.703 131.6
B 2.332 2.49 124.8
5 2.078 2.076 140.18
6 1.997 0.308 130.72
7 2.169 0.268 111.8
8 2.076 2.187 138.46
A 0.208 92.88

34. EJERCICIO N°02 APLICANDO
CORREGIENDO POR DE LA TIERRA
PTO L (+) C
L(+)
corregi
do
NIVEL L(-) C
L(-)
corregi
do
COTA (m) d(m) ai Ci
COTA
COMPENSAD
A
A 0.209 0.0001 0.2091 3660.2091 3660.0000
1 1.493 0.0001 1.4931 3659.8071 1.895 0.0001 1.8951 3658.3140 80 80 0.0036 3658.3176
2 1.619 0.0001 1.6191 3660.1141 1.312 0.0001 1.3121 3658.4950 78.4 158.4 0.0072 3658.5022
3 1.24 0.0003 1.2403 3658.6413 2.713 0.0001 2.7131 3657.4010 92.1 250.5 0.0114 3657.4124
4 0.896 0.0003 0.8963 3656.8343 2.703 0.0003 2.7033 3655.9380 131.6 382.1 0.0174 3655.9554
B 2.332 0.0003 2.3323 3656.6763 2.49 0.0003 2.4903 3654.3440 124.8 506.9 0.0231 3654.3671
5 2.078 0.0003 2.0783 3656.6783 2.076 0.0003 2.0763 3654.6000 140.18 647.08 0.0294 3654.6294
6 1.997 0.0002 1.9972 3658.3672 0.308 0.0003 0.3083 3656.3700 130.72 777.8 0.0354 3656.4054
7 2.169 0.0003 2.1693 3660.2683 0.268 0.0002 0.2682 3658.0990 111.8 889.6 0.0405 3658.1395
8 2.076 0.0001 2.0761 3660.1571 2.187 0.0003 2.1873 3658.0810 138.46 1028.06 0.0468 3658.1278
A 0.208 0.0001 0.2081 3659.9490 92.88 1120.94 0.0510 3660.0000
16.111
1 16.1621 1120.94

35. NIVELACIÓN INDIRECTA
•Este método se basa en el uso de un
instrumento u operación matemática
mediante el cual se calcula indirectamente el
desnivel entre dos puntos.
•Se emplea cuando no se requiere tanta
precisión como para optar por la nivelación
directa.

36. NIVELACIÓN TRIGONOMETRICA
• La trigonometría es el principio fundamental en este tipo de nivelación, en
este método es preciso contar como datos: el ángulo “𝛼” y la distancia
inclinada entre A y B o la correspondiente proyectada al horizonte, el
objetivo es calcular el desnivel ∆ℎ entre dos puntos.
𝛼
∆ℎ =

38. CORRECCIÓN DE NIVEL
APARENTE
• Debido a curvatura terrestre y la refracción atmosférica
• 𝐶 =
6
14
(
𝐷2
𝑅
)

39. NIVELACIÓN BAROMÉTRICA
• Es método física en el cual se utiliza la presión, a mayor altura disminuye la
presión
• ∆ℎ = 10.5∆𝑃, donde
• ∆ℎ = 𝐷𝑖𝑓𝑒𝑟𝑒𝑛𝑐𝑖𝑎 𝑑𝑒 𝑎𝑙𝑡𝑖𝑡𝑢𝑑𝑒𝑠 𝑚
• ∆𝑃 = 𝐷𝑖𝑓𝑒𝑟𝑒𝑛𝑐𝑖𝑎 𝑑𝑒 𝑝𝑟𝑒𝑠𝑖𝑜𝑛𝑒𝑠 𝑚𝑚𝐻𝑔

40. NIVELACIÓN BAROMETRICA
•Otras formulas:
• 𝐷𝑜𝑛𝑑𝑒;
•FORMULA SIMPLIFICADA DE LAPLACE
• 𝑍 𝐵𝐴 = 18400 log
𝑃 𝐴
𝑃 𝐵
(1 + 0.004
𝑇 𝐴+𝑇 𝐵
2
)
• 𝐹𝑂𝑅𝑀𝑈𝐿𝐴 𝐷𝐸 𝐵𝐴𝐵𝐼𝑁𝐸𝑇
• 𝑍 𝐵𝐴 = 16000(
𝑃 𝐴−𝑃 𝐵
𝑃 𝐴+𝑃 𝐵
) (1 + 2
𝑇 𝐴+𝑇 𝐵
1000
)
• 𝑍 𝐵𝐴 = 𝐷𝑒𝑠𝑛𝑖𝑣𝑒𝑙 𝑒𝑛𝑡𝑟𝑒 𝑙𝑜𝑠 𝑝𝑢𝑛𝑡𝑜𝑠 𝐴 𝑦 𝐵 (𝑚𝑒𝑡𝑟𝑜𝑠)
• 𝑃𝐴 = 𝑃𝑟𝑒𝑠𝑖ó𝑛 𝑎𝑡𝑚𝑜𝑠𝑓𝑒𝑟𝑖𝑐𝑎 𝑒𝑛 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝐴 𝑐𝑢𝑎𝑛𝑑𝑜 𝑇 = 0°C (mm Hg)
• 𝑃𝐵 = 𝑃𝑟𝑒𝑠𝑖ó𝑛 𝑎𝑡𝑚𝑜𝑠𝑓𝑒𝑟ica 𝑒𝑛 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 B cuando T = 0°C (mm Hg)
• 𝑇𝐴 = 𝑇𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑎 𝑑𝑒𝑙 𝑎𝑖𝑟𝑒 en el punto A
• 𝑇𝐵 = 𝑇𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑎 𝑑𝑒𝑙 𝑎𝑖𝑟𝑒 𝑒𝑛 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝐵

41. EJERCICIO N° 03
• Se ha medido la presión atmosférica en los puntos A y B. Los datos
obtenidos son los siguientes:
• 𝑃𝐴 = 760𝑚𝑚𝐻𝑔, 𝑇𝐴 = 22°𝐶
• 𝑃𝐵 = 780𝑚𝑚𝐻𝑔, 𝑇𝐵 = 25°𝐶
• Calcular el desnivel aplicando la fórmula simplificada de Laplace y de
babiner.

42. RED DE NIVELACIÓN
• Cuando un conjunto de circuitos cerrados dependen unos de otros, es decir
están enlazados entre si, constituyen una red de nivelación.
• En tal situación es preciso ajustar los desniveles entre cada dos puntos para
que por uno u otro camino resulten iguales.
• Para dicho ajuste es posible usar el método de mínimos cuadrados el cual
implica a la solución de un número de ecuaciones de condición como
circuitos existentes en la red; no obstante es posible usar el método de
aproximaciones sucesivas para llegar al mismo objetivo.

43. EJERCICIO N° 04
CIRCUITO LADO
DISTANCIA ITERACION I
L(Km) % DESNIVEL CORRECCION DESN CORREG
I
AB 0.850 33.865 12.179 0.005 12.184
BC 0.660 26.295 -7.324 0.004 -7.320
CA 1.000 39.840 -4.870 0.006 -4.864
TOTAL 2.510100.000 -0.015 0.015 0.000

44. EJERCICIO N° 04
CIRCUITO LADO
DISTANCIA ITERACION I
L(Km) % DESNIVEL CORRECCION DESN CORREG
II
CB 0.660 23.571 7.320 0.002 7.322
DC 0.910 32.500 -15.172 0.003 -15.169
BD 1.230 43.929 7.843 0.004 7.847
TOTAL 2.800100.000 -0.009 0.009 0.000

45. CIRCUITO LADO
DISTANCIA ITERACION I
L(Km) % DESNIVEL CORRECCION
DESNIVEL
CORREGIDO
PERIMETRAL
AB 0.850 21.303 12.184 0.000 12.184
BD 1.230 30.827 7.847 0.001 7.848
DC 0.910 22.807 -15.169 0.000 -15.169
CA 1.000 25.063 -4.864 0.001 -4.863
TOTAL 3.990 100.000 -0.002 0.002 0.000

46. RED DE NIVELACIÓN
CIRCUIT
O
LADO
DISTANCIA ITERACION I ITERACON II ITERACON III
L(Km) % DV
CORRE
CCION
DV
CORREG DV
CORREC
CION
DESN
CORREG DV
CORREC
CION
DV
CORREG
PERIMETRAL

47. METODOS DE NIVELACIÓN
GEOMÉTRICA
• MÉTODO DE LA DOBLE LIBRETA SIMULTANEA
• El método esta basado en que se realiza simultáneamente dos nivelaciones
compuestas por diferentes caminos, teniendo como punto conocido A y
punto por conocer B
• MÉTODO DE LOS TRES HILOS
• Este método se basa en que se realice el promedio de las lecturas de los
tres hilos entonces la vista atrás y adelante seria
• 𝐿 + =
𝐼𝑠+𝐼 𝑚+𝐼 𝑖
3
𝐿 − =
𝐼𝑠+𝐼 𝑚+𝐼 𝑖
3

48. INSTRUMENTOS

49. DEMOSTRACIÓN DE LA DISTANCIA HORIZONTAL
La relación f/h es la constante distancio
métrico K, con un valor de 100 para facilitar
el calculo de la distancia
Del grafico, se tiene
Siendo:
𝐷 = 𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 𝑒𝑛𝑡𝑟𝑒 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝑑𝑒 𝑒𝑠𝑡𝑎𝑐𝑖ó𝑛 "E" 𝑦 "𝑀" 𝑝𝑢𝑛𝑡𝑜 𝑑𝑒 𝑚𝑖𝑟𝑎
𝑓 = 𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 𝑓𝑜𝑐𝑎𝑙 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑒
ℎ = 𝑆𝑒𝑝𝑎𝑟𝑎𝑐𝑖ó𝑛 𝑒𝑛𝑡𝑟𝑒 𝑒𝑙 𝑟𝑒𝑡𝑖𝑐𝑢𝑙𝑜 𝑠𝑢𝑝𝑒𝑟𝑖𝑜𝑟 𝑦 𝑒𝑙 𝑖𝑛𝑓𝑒𝑟𝑖𝑜𝑟 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑒
𝐻 = 𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 𝑑𝑒 𝑚𝑖𝑟𝑎 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡𝑎𝑑𝑎 𝑝𝑜𝑟 𝑙𝑜𝑠 𝑟𝑒𝑡𝑖𝑐𝑢𝑙𝑜𝑠 = 𝐼𝑠 − 𝐼𝑖

50. PENDIENTES Y BUZAMIENTOS
• Se define como buzamiento (buzamiento
real) de un estrato el ángulo formado por
la línea de máxima pendiente contenida
en el plano del estrato y su proyección
sobre un plano horizontal
• Pendiente es el ángulo de inclinación con
respecto a un plano horizontal de una
carretera, labor o terreno expresado en grado
y porcentajes.
• Gradiente ángulo de inclinación de un trazo
con respecto a un plano horizontal expresado
en grados

51. EJERCICIO N° 05
• Se tienen dos tramos AB y BC, donde se obtuvieron el desnivel y la distancia
horizontal de ambos tramos, por el método de nivelación geométrica
compuesta obteniendo, los siguientes datos:
• 𝐷𝐻𝐴𝐵 = 𝐷𝑅 𝐴𝐵 = 799.169𝑚; 𝐷𝑉𝐴𝐵 = 17.765𝑚
• 𝐷𝐻 𝐵𝐶 = 𝐷𝑅 𝐵𝐶 = 826.140𝑚; 𝐷𝑉𝐵𝐶 = 14.694𝑚
• Calcular la distancia real de AB+BC, la pendiente AB y BC, la gradiente AB y
BC

52. PERFIL LONGITUDINAL
En ingeniería es común hacer nivelación de alineación para
proyectos de carreteras, canales acueductos, etc. Estas
nivelaciones reciben el nombre de nivelación de perfiles
longitudinales y se toman a lo largo del eje del proyecto
En el caso de nivelaciones para proyectos viales, la
nivelación se hace a lo largo del eje de proyecto con puntos
de mira a cada 20 o 40m, dependiendo del tipo de terreno
más en los puntos de quiebre brusco del terreno.

53. NIVELACIÓN EN PERFIL
LONGITUDINAL
• Los puntos de cambio y las estaciones deben ubicarse de
manera de abarcar la mayor cantidad posible de puntos
intermedios. Debe tenerse cuidado en la escogencia de los
puntos de cambio ya éstos son los puntos de enlace o de
transferencia de cotas. Deben ser puntos firmes en el
terreno, o sobre estacas de madera, vigas de puentes, etc
• Siendo los puntos de cambio puntos de transferencia de
cotas, en ellos siempre será necesario tomar una lectura
adelante desde una estación y una lectura atrás desde la
estación siguiente.

54. EJERCICIO N° 06 DE NIVELACIÓN
DE PERFIL LONGITUDINAL
En una campo de Haquira se realizo la nivelación longitudinal siendo los datos obtenidos los
mostrados en la figura adjunta

55. EJERCICIO N° 06 METODO
PROPORCIONAL
E PTO
L(+)
corregido
L(-)
Intermedio
L(-)
corregido
COTA
(m)
d(m)
E1
A 0.865 187.526
1 1.543 60.000
2 2.284 160.000
PC1 2.736 3.861 70.000
E2
3 2.043 40.000
4 1.638 150.000
PC2 1.625 0.937 50.000
E3
5 2.174 80.000
6 0.917 140.000
A 0.420 80.000
DATOS DE CAMPO

56. EJERCICIO N° 06 METODO
PROPORCIONAL
𝑪𝒊 = −
𝜺 𝒄×𝒂 𝒊
𝒅𝒕
E PTO
L(+)
corregido
L(-)
Intermedio
L(-)
corregido
NIVEL
COTA
(m)
d (m) ai (m) Ci
COTA
COMPENSAD
A
E1
A 0.865 188.391 187.526
1 1.543
2 2.284
PC1 2.736 3.861 187.266
E2
3 2.043
4 1.638
PC2 1.625 0.937 187.954
E3
5 2.174
6 0.917
A 0.420
SUMA 5.226 5.218
Dif. 0.0080
E PTO
L(+)
corregido
L(-)
Intermedio
L(-)
corregido
NIVEL
COTA
(m)
d (m) ai (m) Ci
COTA
COMPENSAD
A
E1
A 0.865 188.391 187.526
1 1.543 186.848
2 2.284 186.107
PC1 2.736 3.861 187.266 184.530
E2
3 2.043 185.223
4 1.638 185.628
PC2 1.625 0.937 187.954 186.329
E3
5 2.174 185.780
6 0.917 187.037
A 0.420 187.534
SUMA 5.226 5.218
Dif. 0.0080 0.0080
E PTO
L(+)
corregido
L(-)
Intermedio
L(-)
corregido
NIVEL
COTA
(m)
d (m) ai (m) Ci
COTA
COMPENSAD
A
E1
A 0.865 188.391 187.526
1 1.543 186.848 60.000 60.000 186.848
2 2.284 186.107 160.000 220.000 186.107
PC1 2.736 3.861 187.266 184.530 70.000 290.000 -0.003 184.527
E2
3 2.043 185.223 40.000 330.000 -0.003 185.220
4 1.638 185.628 150.000 480.000 -0.005 185.623
PC2 1.625 0.937 187.954 186.329 50.000 530.000 -0.005 186.324
E3
5 2.174 185.780 80.000 610.000 -0.006 185.774
6 0.917 187.037 140.000 750.000 -0.007 187.030
A 0.420 187.534 80.000 830.000 -0.008 187.526
SUMA 5.226 5.218 830.000
Dif. 0.0080 0.0080

57. GRAFICA DE PERFIL LONGITUDINAL

58. EJERCICIO N° 07 METODO POR
PUNTOS DE CAMBIO
E PTO L(+)
corregido
L(-)
Intermedio
L(-)
corregido
d(m) Ci NIVEL
COTA
COMPENSADA
(m)
E1
A 0.865 188.391 187.526
1 1.543 60.000 186.848
2 2.284 160.000 186.107
PC1 2.736 3.861 70.000 -0.004 187.262 184.526
E2
3 2.043 40.000 185.219
4 1.638 150.000 185.624
PC2 1.625 0.937 50.000 -0.004 187.946 186.321
E3
5 2.174 80.000 185.772
6 0.917 140.000 187.029
A 0.420 80.000 187.526
SUMA 5.226 5.218 830.000
Dif. 0.008 0.000

59. EJERCIO N° 08
P L(+) corregido LI corregido L(-) corregido COTA (m) d(m)
A 1.030 3600
1 1.353 20
2 1.5 20
3 1.93 20
B 1.67 1.883 9
4 1.785 11
5 1.542 20
6 1.336 20
7 1.037 20
8 0.868 20
C 2.45 0.832 16.65
9 2.271 3.35
10 1.983 20
11 1.857 20
12 1.372 20
13 1.084 20
D 0.825 1.02 6.05
14 1.26 13.95
15 1.565 20
E 1.193 1.717 17.5
16 1.229 2.5
17 1.452 20
18 1.497 20
A 1.622 16.5
Se tiene los siguientes datos de
campo de una nivelación
longitudinal mostrados en el
cudro adjunto, se pide calcular
las cotas compensadas
utilizando el método
proporcional y método de
punto de cambio

60. PERFIL TRANSVERSAL
• Son perfiles perpendiculares al perfil longitudinal, que se toman cada 20 a
40 metros, o donde hay variaciones de cota considerables, con un ancho
desde el eje de 10 metros derecha y 10 metros izquierda, donde se va
midiendo sus ángulos de inclinación (pendientes), derecha e izquierda en
para luego calcular sus áreas.
• En combinación con el perfil longitudinal se puede calcular el volumen

61. SECCIONES TRANSVERSALES
TÍPICAS
CORTE O EXCAVACIÓN (CORTE CERRADO)
RELLENO O TERRAPLEN
CORTE EN LADERA
MIXTO O A MEDIA LADERA

62. CALCULO DE VOLUMEN

63. EJERCICIO N° 09
• Calcular las áreas de corte y relleno, para un tramo de 20m de carretera, si
la carretera tiene una pendiente 1.2%, además se tiene un ancho de
carretera de 10m a la izquierda, con una pendiente de 1% y 10m a la
derecha con pendiente de -0.5%, en la progresiva 00.00, y una pendiente
de 1.5% derecha y -1% izquierda en la progresiva 20.00 mcon ancho de
10m a ambos lados, con pendiente de 0%. Si la pendiente pedida para la
caída de agua es de 0.5% a la derecha e izquierda. CALCULAR EL
VOLUMEN DE MOVIENTO DE TIERRA, PARA LA PENDIENTE PEDIDA SI LA
PENDIENTE DEL SITIO ES DE 0%