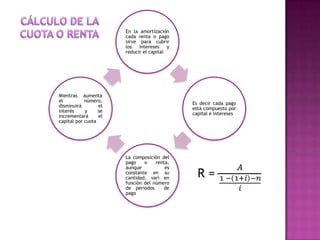
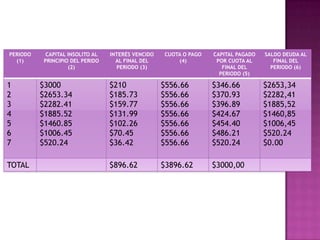
Este documento presenta información sobre el proceso de amortización gradual para cancelar una deuda a través de pagos periódicos. Explica cómo cada pago se divide entre capital e intereses, disminuyendo el saldo insoluto con el tiempo. También muestra cómo calcular el valor de los pagos, construir una tabla de amortización, y determinar el saldo insoluto para cualquier período. Finalmente, discute los derechos del acreedor y deudor a medida que la deuda se va pagando gradualmente a través del tiempo.

1. UNIVERSIDAD POLITÈCNICA ESTATAL DE CARCHI
ESCUELA:
COMERCIO EXTERIOR
MATERIA:
MATEMÁTICA
DANIELA HERNANDEZ
NIVEL:
CUARTO “A”

2. OBJETIVO:
 analizar la aplicación el proceso de
amortización gradual, así como el
proceso de formación de fondos
de valor futuro.

3. Es el proceso de cancelar una deuda y sus intereses por
medio de pagos de periodos.
AMORTIZAR: Se dice que un documento que causa
intereses está amortizado cuando todas las obligaciones
contraídas son liquidadas mediante una serie de pagos
hechos en intervalos de tiempos iguales

4. En la amortización
cada renta o pago
sirve para cubrir
los intereses y
reducir el capital
Mientras aumenta
el número,
Es decir cada pago
disminuirá el
está compuesto por
interés y se
capital e intereses
incrementará el
capital por cuota
La composición del
pago o renta,
aunque es
constante en su
cantidad, varí en
función del número
de periodos de
pago

5.  Por ejemplo, para calcular el valor de pago semestral de
una empresa que consigue un préstamo de $3000 con una
tasa de interés del 14% anual capitalizable
semestralmente, el cual será amortizado mediante pagos
iguales, cada semestre, durante 3 años y 6 meses, se
realiza el siguiente procedimiento.
A = $3000
R=?

6. La parte de la
deuda no
cubierta en una
fecha dada se
conoce como
saldo insoluto o
capital insoluto
en la fecha
CAPITAL
INSOLUTO El capital insoluto,
Y TABLA justamente de que
se ha efectuado un
DE pago, es el valor
AMORTIZA presente de todos
los pagos que aun
CIÓN faltan por hacerse
La parte de la deuda
no pagada constituye
el saldo insoluto,
como se muestra en
la siguiente tabla
denominada “ TABLA
DE AMORTIZACIÓN”

7. PERIODO CAPITAL INSOLITO AL INTERÉS VENCIDO CUOTA O PAGO CAPITAL PAGADO SALDO DEUDA AL
(1) PRINCIPIO DEL PERIDO AL FINAL DEL (4) POR CUOTA AL FINAL DEL
(2) PERIODO (3) FINAL DEL PERIODO (6)
PERIODO (5)
1 $3000 $210 $556.66 $346.66 $2653,34
2 $2653.34 $185.73 $556.66 $370.93 $2282,41
3 $2282.41 $159.77 $556.66 $396.89 $1885,52
4 $1885.52 $131.99 $556.66 $424.67 $1460,85
5 $1460.85 $102.26 $556.66 $454.40 $1006,45
6 $1006.45 $70.45 $556.66 $486.21 $520.24
7 $520.24 $36.42 $556.66 $520.24 $0.00
TOTAL $896.62 $3896.62 $3000,00

8. El interés vencido al final del primer periodo es :
 I = Cit I= 3000(0.07)(1) = $210,00
El capital pagado al final del primer periodo es :
o Cuota – Interés = 556.66 – 210.000 = $346,66
El capital insoluto para el segundo periodo, que es a la vez el saldo de la deuda al final del primer
periodo es:
Capital al principio del primer periodo - Capital pagado al final de primer periodo
 = 3000 – 346,66 = $2653,34
El interés vencido al final del segundo periodo es:
 I= 2653,34 (0.07) (1) = $185,73
El capital pagado al final del segundo periodo es:
 556,66 – 185,73 = $370,92
El capital insoluto para el tercer periodo es:
 2653,34 – 370,93 = $2282,41

9. Sea P el saldo insoluto, m el
número de cuotas pagadas,
n el número total de cuotas
y k el número de cuotas que
quedan por pagar.
El capital insoluto Con base en el ejemplo
puede calcularse anterior, calculemos el
para cualquier capital insólito después
del quinto pago que
periodo utilizando la corresponde al valor
fórmula del valor de actual de dos periodos
una anualidad, con que faltan por
ligerea variaciones descubrirse
CÁLCULO DEL SALDO
INSOLUTO

11. RECOSNTRUCCIÓN DE LA TABLA DE
AMORTIZAQCIÓN
La tabla de amortización puede rehacerse en
cualquier periodo; para ello es necesario
calcular primero el saldo insoluto en el periodo
que queremos rehacer la tabla, y luego el
interés y el capital que correspondan a la
determinada cuota

12.  Calculamos ahora la distribución del interés y capital de la
cuota 6 del ejemplo citado anteriormente. Puesto que el
saldo insoluto es $1.006,45 al comienzo del sexto periodo,
el interés será:
( 1.006,45) ( 0.07) = $70,45
El capital será
Cuota – Interés = 556,66 – 70,45 = $486,21
Y la tabla puede rehacerse así:
PERIODO CAPITAL INTERÉS CUOTA CAPITAL SALDO DEUDA
INSOLUTO VENCIDO $ PAGADO AL FINAL DEL
$ $ $ PERIODO $
6 1.006,45 70,45 556,66 486,21 520,24
7

13. 

14. PERIODO Saldo insoluto inicio INTERÉS RENTA CAPITAL PAGADO SALDO DEUDA
periodo FINAL DEL
PERIODO
1 $4500,00 $270,000 $915,13 $645,13 $3854,87
2 $3854,87 $231,29 $915,13 $683,84 $3171,03
3 $3171,02 $190,26 $915,13 $724,87 $2446,16
4 $2446,16 $146,77 $915,13 $768,36 $1677,80
5 $1677,80 $100,67 $915,13 $814,46 $863,33
6 $863,33 $51,80 $915,13 $863,33 $0.00
TOTAL $990,78 $5490,78 $4500
 CALCULEMOS EL SALDO INSOLUTO INMEDIATAMENTE
DESPUÉS DEL PAGO 4 Y LA DISTRIBUCIÓN DEL CAPITAL E
INTERESES DE LA CUOTA 5.

16. Con frecuencia se
realizan
préstamos a largo
plazo con la
PERIODO DE
modalidad de GRACIA
amortización
gradual
Esto consiste en
que se incluye un
periodo sin que se
paguen cuotas, el
cual se denomina
periodo de gracia

17.  Una empresa consigue un préstamo por un valor de $20000 a 10 años de plazo,
incluidos 2 de gracia, con una tasa de interés del 9 ½% anual capitalizable
semestralmente, para ser pagado mediante cuotas semestrales por el sistema
de amortización gradual. La primera cuota semestral y el saldo insoluto
inmediatamente después de haber pagado la cuota 5 y la distribución de la
cuota 6, en lo que respecta al capital e intereses.

18. A CONTINUACIÓN SE PRESENTA LA GRÁFICA PARA EL SALDO INSOLUTO
 K= 16 – 5 = 11
LA COMPOSICIÓN DE LA CUOTA 6 SERÁ , TANTO DE INTERÉS COMO DE
CAPITAL:
 I = (15.256,75)(0,0475) = $724,69 de interés
 Cuota – interés = Capital pagado por cuota
 1812,70 - 724,69= $1088,01

19. Cuando se adquiere un bien
a largo plazo o se está
DERECHOS DEL pagando una deuda por el La relación
ACREEDOR Y sistema de amortización acreedor deudor se
gradual, generalmente se puede representar
DEL DEUDOR quiere conocer qué parte de
mediante la
la deuda está ya pagada en
determinado tiempo, o siguiente ecuación
también cuales son los
derechos del acreedor o los
derechos del deudor
Derechos del
acreedor + Derechos
del deudor
= DEUDA
SALDO INSOLUTO +
PARTE AMORTIZADA =
DEUDA ORIGINAL

20.  Una persona adquiere una propiedad mediante un
préstamo hipotecario de $120000 a 15 años de plazo. Si
debe pagar la deuda en cuotas mensuales iguales y se
considera una tasa de interés del 1,5% mensual, ¿Cuáles
serán los derechos del acreedor y del deudor
inmediatamente después de haber pagado la cuota?
 Se calcula el valor de la cuota mensual:
i= 0.015 n= (15)(12) = 180 cuotas