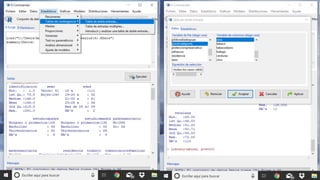
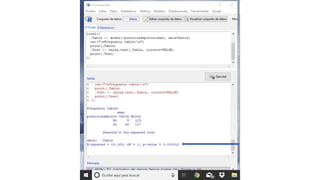
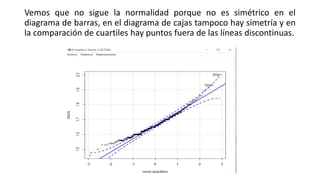
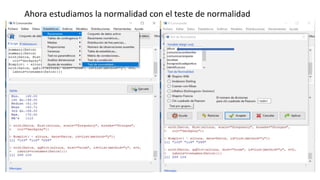
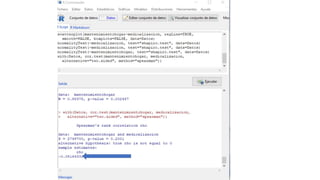
Este documento resume los pasos para analizar diferentes tipos de variables cualitativas y cuantitativas. Explica cómo realizar tablas de contingencia y calcular el grado de libertad para variables cualitativas dicotómicas. Luego, analiza variables cualitativas politómicas y cuantitativas evaluando la normalidad y homocedasticidad para seleccionar las pruebas estadísticas apropiadas. Finalmente, examina dos variables cuantitativas evaluando la linealidad y fuerza de correlación.

1. ANALISIS DE DOS VARIABLES
CUALITATIVAS

2. • PRIMERO CARGAMOS EL CONJUNTO DE DATOS DE ACTIVOS EN
SALUD:

3. Nos metemos en estadísticos, luego en resúmenes
y por último a conjunto de datos activos y
aceptamos.

5. Elegimos las dos variables cualitativas.
Sexo y practicadeporte son las variables que hemos elegido.
Vamos a estadísticos, seleccionamos: tabla de contingencia y
tabla de doble entrada.
Cuando se abre la tabla de doble entrada, elegimos
practicadeporte en la variable fila, y sexo en la variable
columna. Por último, clicamos ACEPTAR.

7. Como es una tabla de 2x2, calculamos el grado de libertad, que es:
filas-1 x columnas-1. en este caso, el grado de libertad es 1.
Como el valor de p es menor al valor de p estimado que es 0.05 que es
el valor de p que da un 95% de confianza, rechazamos la hipótesis nula
que establece la no asociación y aceptamos la hipótesis alternativa que
establece la asociación.

9. ANALISIS DE VARIABLES
CUALITATIVA Y CUANTITATIVA

10. Cargamos el conjunto de datos activos.
Elegimos las variables: botellón y altura.
1. Tenemos que ver si la cualitativa es dicotómica o politómica.
Botellon seria politómica porque tiene más de dos categorías.
2. Sobre la cuantitativa, vamos a estudiar su normalidad y la
homocedasticidad.

11. En primer lugar vamos a analizar la normalidad mediante gráficos.
Comenzamos con el histograma:

14. Proseguimos por el diagrama de cajas

15. Por último comprobamos la normalidad con la comparación de
cuartiles:

16. Vemos que no sigue la normalidad porque no es simétrico en el
diagrama de barras, en el diagrama de cajas tampoco hay simetría y en
la comparación de cuartiles hay puntos fuera de las líneas discontinuas.

17. Ahora estudiamos la normalidad con el teste de normalidad

18. P nos sale que es menor a 0.05, así que rechazamos la hipótesis nula.
Por lo tanto no hay normalidad.

19. Como no sigue la normalidad, podemos realizar los test
correspondientes sin estudiar la homocedasticidad a través del test de
Levene, pero la vamos a estudiar. El test de Leve estudia la igualdad
entre las varianzas.

21. Al ser mayor que 0.05, no alcanza la significación estadística y
aceptamos la hipótesis nula, por lo que hay igualdad entre varianzas.
Si falla o la normalidad o la homocedasticidad, tenemos que hacer un
test no paramétrico. Como en este caso es una variable cualitativa
politómica, usamos el test de Kruskal-wallis.

24. La p no alcanza la significación estadística por lo que aceptamos la
hipótesis nula. Esto significa que no hay relación entre el botellón y la
altura.

25. ANALISIS BIVARIADO DE DOS
CUANTITATIVAS

26. Volvemos a cargar el conjunto de datos y elegimos dos variables
cuantitativas. En este caso hemos elegido: medicalización y
mantenimeintohogar.

27. Ahora estudiamos la linealidad de las variables mediante métodos
gráficos.
En gráficas, clicamos en diagrama de dispersión.

30. Vemos que hay linealidad. La pendiente de la línea es negativa porque
vemos que es descendente.

31. Ahora vamos a estudiar la normalidad por los test de normalidad
directamente ya que con las gráficas lo hemos hecho en trabajos
anteriores.

34. La p tiene un valor menor que 0.05, por lo tanto, rechazamos la
hipótesis nula y aceptamos la alternativa, que dice que no sigue la
distribución normal.
Como no hay normalidad, utilizamos el test no paramétrico de
Spearman para saber la fuerza de la correlación.

37. Hemos hecho el test no paramétrico de Spearman y nos da rho un
valor negativo que se acerca mucho a 0, por lo tanto, la correlación es
muy débil.