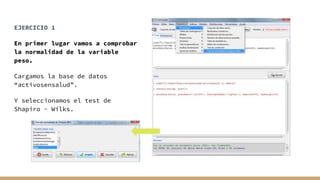
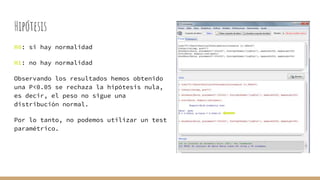
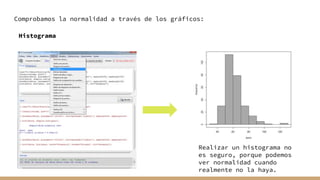
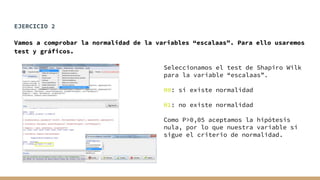
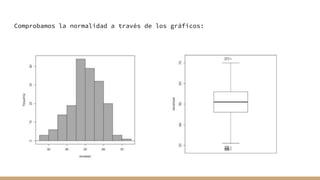
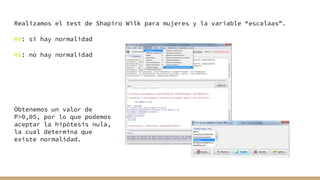
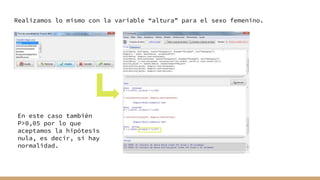
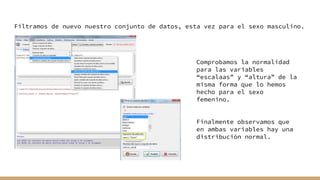
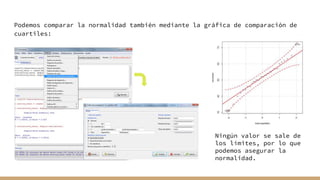
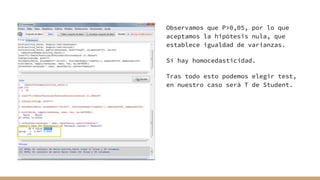
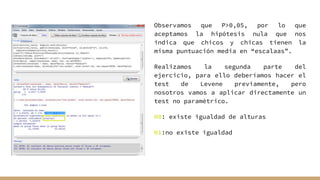
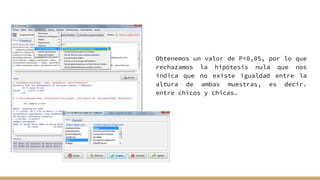
El documento aborda el análisis bivariado de variables cualitativas y cuantitativas, describiendo pruebas estadísticas como t de Student, ANOVA y pruebas no paramétricas como Mann-Whitney. Se presentan ejercicios prácticos que incluyen la comprobación de normalidad con el test de Shapiro-Wilk y la comparación de medias entre grupos, incluyendo la verificación de homocedasticidad mediante el test de Levene. Finalmente, se realizan conclusiones sobre la igualdad de medias y varianzas entre distintos grupos de datos.

1. R Commander
Análisis bivariado:
variable cualitativa y
cuantitativa
María Ruiz Gallardo

2. Seminario 8
Este tipo de análisis es sumamente frecuente en todos los ámbitos, puesto que
con frecuencia nos interesa responder si…
★ ¿Los valores medios de nuestra variable cuantitativa son similares o no a
un valor medio de referencia?
★ ¿Los valores medios de una variable cuantitativa son similares o no entre
las diferentes categorías de una variable cualitativa?
★ ¿Los valores medios de nuestra variable cuantitativa son similares o no
antes y después de un evento/prueba/intervención?

3. Test a aplicar...
Paramétricos
★ T de student para 1 o dos muestras (o categorías)
★ ANOVA (para más de dos muestras o categorías independientes)
No paramétricos
★ Prueba U de Mann-Whitney (muestras independientes). T de student
★ Test Wilconxon (muestras independientes y muestras apareadas). T de
student
★ Test Kruskal-Wallis (más de dos muestras o categorías). Anova

4. EJERCICIO 1
En primer lugar vamos a comprobar
la normalidad de la variable
peso.
Cargamos la base de datos
“activosensalud”.
Y seleccionamos el test de
Shapiro - Wilks.

5. Hipótesis
H0: si hay normalidad
H1: no hay normalidad
Observando los resultados hemos obtenido
una P<0.05 se rechaza la hipótesis nula,
es decir, el peso no sigue una
distribución normal.
Por lo tanto, no podemos utilizar un test
paramétrico.

6. Comprobamos la normalidad a través de los gráficos:
Histograma
Realizar un histograma no
es seguro, porque podemos
ver normalidad cuando
realmente no la haya.

7. Diagrama de caja

8. EJERCICIO 2
Vamos a comprobar la normalidad de la variables “escalaas”. Para ello usaremos
test y gráficos.
Seleccionamos el test de Shapiro Wilk
para la variable “escalaas”.
H0: si existe normalidad
H1: no existe normalidad
Como P>0,05 aceptamos la hipótesis
nula, por lo que nuestra variable si
sigue el criterio de normalidad.

9. Comprobamos la normalidad a través de los gráficos:

10. EJERCICIO 3
¿Es la media de las puntuaciones
obtenidas en “escalaas” igual a
45 puntos?
Una vez comprobada la normalidad
utilizamos el test paramétrico de
T de Student.
H0: la media de valores es 45
H1: la media no es 45
La T=9.0704 y P<0.05, por lo que
rechazamos la hipótesis nula, por
tanto se aleja de 45.

11. EJERCICIO 4
Comparar medias de muestras
independientes:
★ Chicos y chicas tienen la
misma puntuación media en
“escalaas”
★ Chicos y chicas tienen la
misma altura media
Filtramos la variable sexo para
comprobar la normalidad de
hombres y mujeres por separado.

12. Realizamos el test de Shapiro Wilk para mujeres y la variable “escalaas”.
H0: si hay normalidad
H1: no hay normalidad
Obtenemos un valor de
P>0,05, por lo que podemos
aceptar la hipótesis nula,
la cual determina que
existe normalidad.

13. Realizamos lo mismo con la variable “altura” para el sexo femenino.
En este caso también
P>0,05 por lo que
aceptamos la hipótesis
nula, es decir, si hay
normalidad.

14. Filtramos de nuevo nuestro conjunto de datos, esta vez para el sexo masculino.
Comprobamos la normalidad
para las variables
“escalaas” y “altura” de la
misma forma que lo hemos
hecho para el sexo
femenino.
Finalmente observamos que
en ambas variables hay una
distribución normal.

15. Podemos comparar la normalidad también mediante la gráfica de comparación de
cuartiles:
Ningún valor se sale de
los límites, por lo que
podemos asegurar la
normalidad.

16. Por último comprobamos la homocedasticidad, que se refiere a la igualdad de
varianzas. Para ello usaremos el test de Levene.
Para realizar el test de Levene volvemos a cargar el conjunto de datos entero.
Queremos saber si las varianzas son muy
dispares entre hombres y mujeres.
H0: igualdad de varianzas
H1: varianzas distintas

17. Observamos que P>0,05, por lo que
aceptamos la hipótesis nula, que
establece igualdad de varianzas.
Sí hay homocedasticidad.
Tras todo esto podemos elegir test,
en nuestro caso será T de Student.

18. Seleccionamos T de Student para muestras independientes porque vamos a
comparar grupos distintos.

19. Observamos que P>0,05, por lo que
aceptamos la hipótesis nula que nos
indica que chicos y chicas tienen la
misma puntuación media en “escalaas”.
Realizamos la segunda parte del
ejercicio, para ello deberíamos hacer el
test de Levene previamente, pero
nosotros vamos a aplicar directamente un
test no paramétrico.
H0: existe igualdad de alturas
H1:no existe igualdad

20. Obtenemos un valor de P<0,05, por lo que
rechazamos la hipótesis nula que nos
indica que no existe igualdad entre la
altura de ambas muestras, es decir.
entre chicos y chicas.

21. FIN