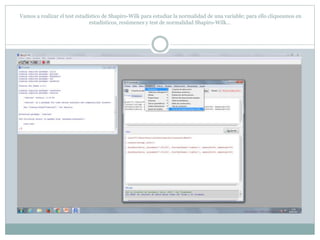
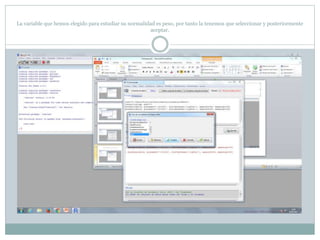
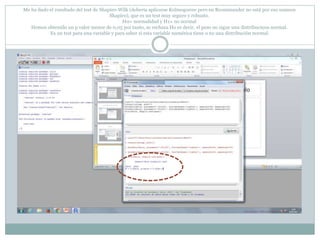
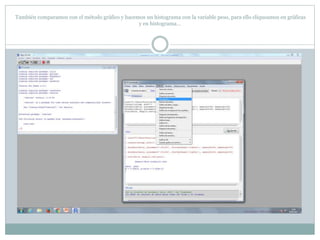
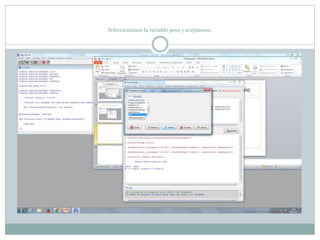
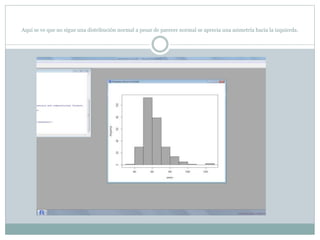
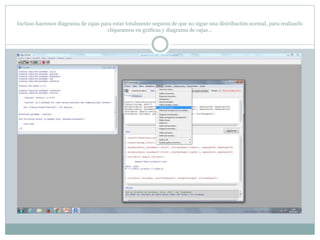
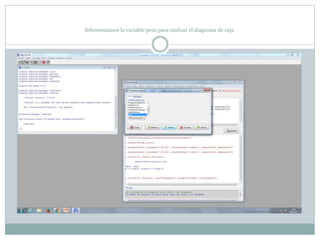
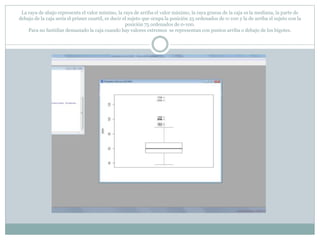
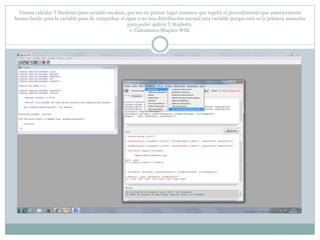
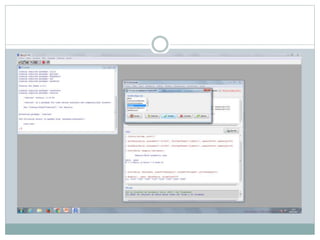
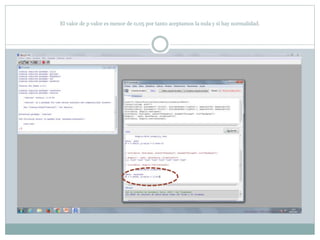
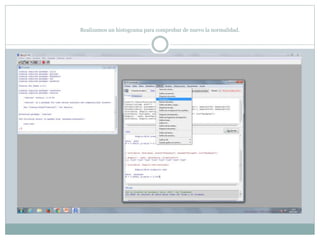
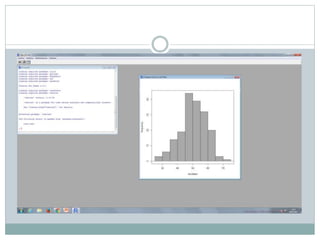
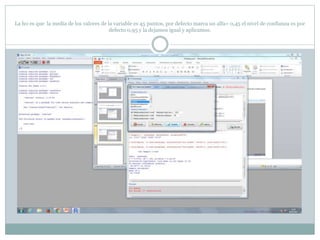
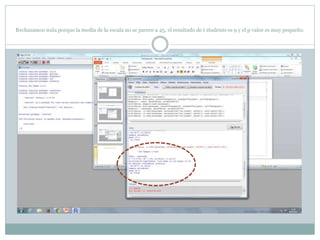
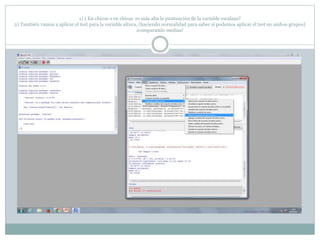
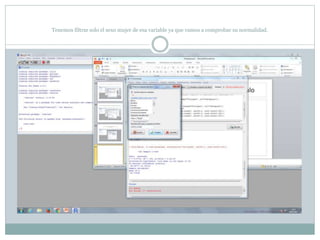
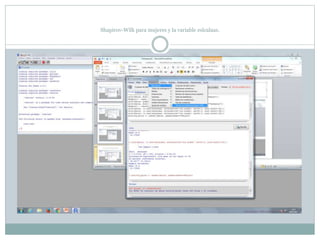
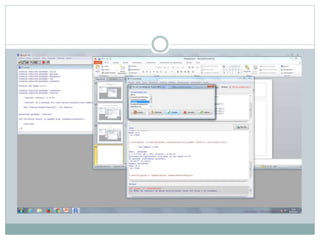
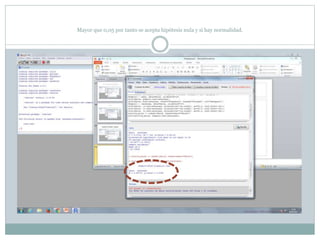
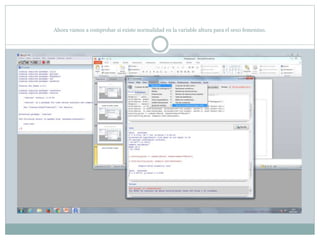
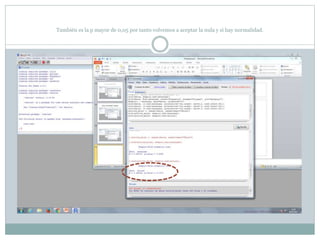
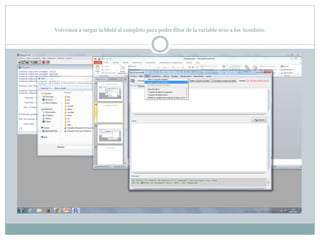
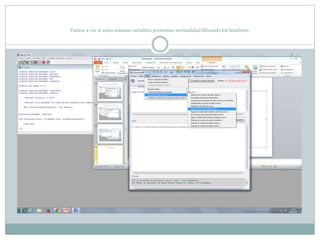
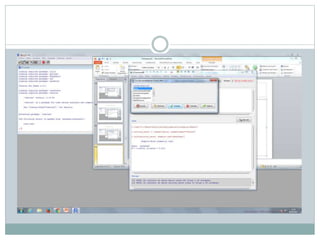
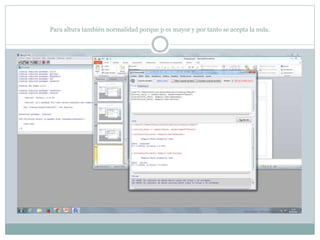
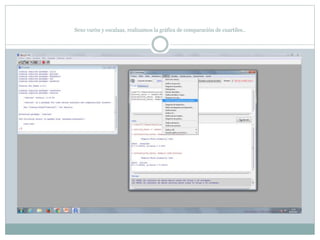
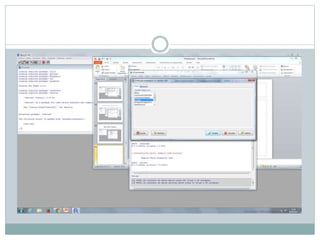
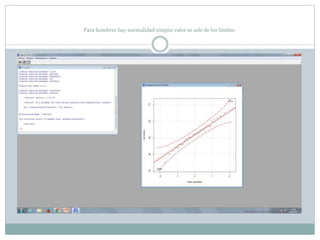
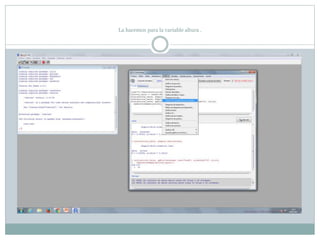
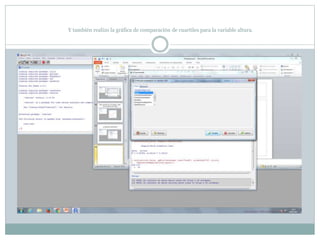
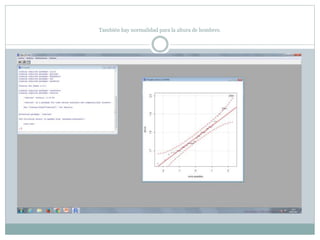
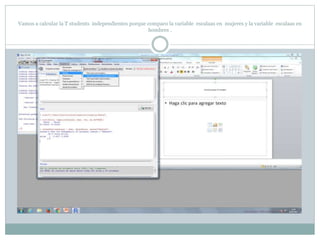
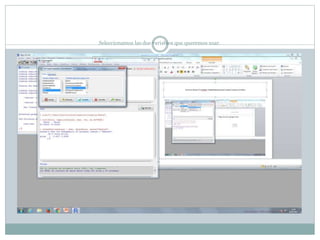
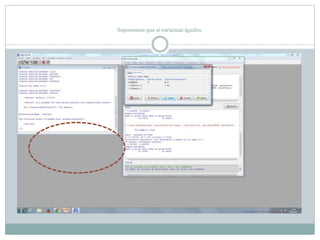
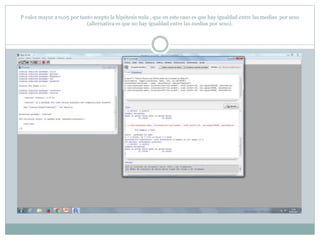
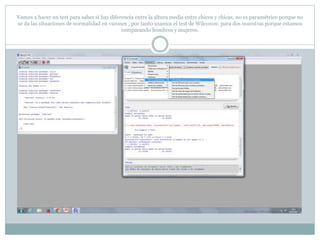
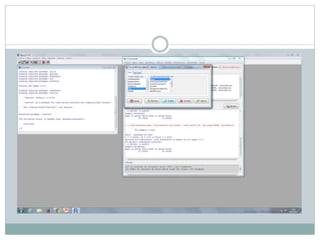
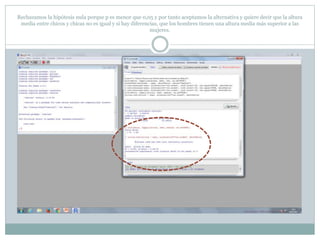
Este documento describe cómo realizar pruebas estadísticas para analizar datos y comparar grupos. Explica cómo usar las pruebas de Shapiro-Wilk, histograma y diagrama de cajas para verificar la normalidad de las variables. Luego aplica la prueba t de Student para datos apareados y grupos independientes y la prueba de Levene para comprobar la homocedasticidad. Finalmente, concluye que no hay diferencias significativas en las puntuaciones medias de escalaas entre hombres y mujeres, pero que los hombres tienen una altura media signific

1. TABLAS ESTADÍSTICAS. T DE
STUDENT PARA DATOS
APAREADOS Y PARA GRUPOS
INDEPENDIENTES. NORMALIDAD.
HOMOCEDASTICIDAD
Análisis bivariado: variable
cualitativa y cuantitativa.

2. En primer lugar, cargamos la base de datos activos en salud.

5. Vamos a realizar el test estadístico de Shapiro-Wilk para estudiar la normalidad de una variable; para ello cliqueamos en
estadísticos, resúmenes y test de normalidad Shapiro-Wilk…

6. La variable que hemos elegido para estudiar su normalidad es peso, por tanto la tenemos que seleccionar y posteriormente
aceptar.

7. Me ha dado el resultado del test de Shapiro-Wilk (debería aplicarse Kolmogorow pero en Rcommander no está por eso usamos
Shapiro), que es un test muy seguro y robusto.
H0= normalidad y H1= no normal
Hemos obtenido un p valor menor de 0,05 por tanto, se rechaza Ho es decir, el peso no sigue una distribuciçon normal.
Es un test para una variable y para saber si esta variable numérica tiene o no una distribución normal.

8. También comparamos con el método gráfico y hacemos un histograma con la variable peso, para ello cliqueamos en gráficas
y en histograma…

9. Seleccionamos la variable peso y aceptamos.

10. Aquí se ve que no sigue una distribución normal a pesar de parecer normal se aprecia una asimetría hacia la izquierda.

11. Incluso hacemos diagrama de cajas para estar totalmente seguros de que no sigue una distribución normal, para realizarlo
cliqueamos en gráficas y diagrama de cajas…

12. Seleccionamos la variable peso para realizar el diagrama de caja.

13. La raya de abajo representa el valor mínimo, la raya de arriba el valor máximo, la raya gruesa de la caja es la mediana, la parte de
debajo de la caja sería el primer cuartil, es decir el sujeto que ocupa la posición 25 ordenados de 0-100 y la de arriba el sujeto con la
posición 75 ordenados de 0-100.
Para no fastidiar demasiado la caja cuando hay valores extremos se representan con puntos arriba o debajo de los bigotes.

14. Vamos calcular T Students para variable escalaas, por eso en primer lugar tenemos que repetir el procedimiento que anteriormente
hemos hecho para la variable peso de comprobar si sigue o no una distribución normal esta variable porque esto es la primera asunción
para poder aplicar T Students.
1- Calculamos Shapiro-Wilk.

16. El valor de p valor es menor de 0,05 por tanto aceptamos la nula y si hay normalidad.

17. Realizamos un histograma para comprobar de nuevo la normalidad.

20. También realizamos el diagrama de caja.

23. Vamos a comparar las medias para ver si : ¿la media de las puntuaciones obtenidas en escalasas es diferente o igual a 45?
Vamos a aplicar el test de la T students.

24. La h0 es que la media de los valores de la variable es 45 puntos, por defecto marca un alfa= 0,45 el nivel de confianza es por
defecto 0,95 y la dejamos igual y aplicamos.

25. Rechazamos nula porque la media de la escala no se parece a 45, el resultado de t students es 9 y el p valor es muy pequeño.

26. 1) ¿ En chicos o en chicas es más alta la puntuación de la variable escalaas?
2) También vamos a aplicar el test para la variable altura, (haciendo normalidad para saber si podemos aplicar el test en ambos grupos)
¡comparando medias!

27. Tenemos filtrar solo el sexo mujer de esa variable ya que vamos a comprobar su normalidad.

28. Shapirov-Wilk para mujeres y la variable eslcalaas.

30. Mayor que 0,05 por tanto se acepta hipótesis nula y si hay normalidad.

31. Ahora vamos a comprobar si existe normalidad en la variable altura para el sexo femenino.

33. También es la p mayor de 0,05 por tanto volvemos a aceptar la nula y si hay normalidad.

34. Volvemos a cargar la bbdd al completo para poder filtar de la variable sexo a los hombres.

36. Vamos a ver si estas mismas variables presentan normalidad filtrando los hombres.

38. Realizamos Shapiro-Wilk para la variable escalaas en hombres.

40. En escala p valor es mayor que 0.05, por tanto hay normalidad y aceptamos la hipótesis nula.

41. Vemos la normalidad para la variable altura en hombres.

43. Para altura también normalidad porque p es mayor y por tanto se acepta la nula.

44. Sexo varón y escalaas, realizamos la gráfica de comparación de cuartiles..

46. Para hombres hay normalidad ningún valor se sale de los límites.

47. La hacemos para la variable altura .

48. Y también realizo la gráfica de comparación de cuartiles para la variable altura.

49. También hay normalidad para la altura de hombres.

50. Todavía queda un último paso antes de elegir el test, hay que comprobar homocedasticidad: para esto está el test de Levene.

51. Cargamos de nuevo la base de datos.

53. Vamos a comprobar la homocedasticidad entre las variables sexo y escalaas.

54. Vamos a ver si las varianzas son o no son muy dispares entre hombres y mujeres, mi h0= igualdad de varianzas y h1= varianzas
distintas, el p valor es Pr= 0,48, por tanto aceptamos la hipótesis nula al ser mayor de 0,05; por tanto podemos decir que hay
homocedasticidad y por tanto al cumplir todos los requisitos podemos usar el test paramétrico de T students porque además son dos
grupos paramétricos a comparar.

55. Vamos a calcular la T students independientes porque comparo la variable escalaas en mujeres y la variable escalaas en
hombres .

56. Seleccionamos las dos variables que queremos usar.

57. Suponemos que si varianzas iguales.

58. P valor mayor a 0,05 por tanto acepto la hipótesis nula , que en este caso es que hay igualdad entre las medias por sexo
(alternativa es que no hay igualdad entre las medias por sexo).

59. Vamos a hacer un test para saber si hay diferencia entre la altura media entre chicos y chicas, no es paramétrico porque no
se da las situaciones de normalidad en varones , por tanto usamos el test de Wilcoxon: para dos muestras porque estamos
comparando hombres y mujeres.

61. Rechazamos la hipótesis nula porque p es menor que 0,05 y por tanto aceptamos la alternativa y quiere decir que la altura
media entre chicos y chicas no es igual y si hay diferencias, que los hombres tienen una altura media más superior a las
mujeres.

62. FIN
Natalia Rodríguez Bereginal