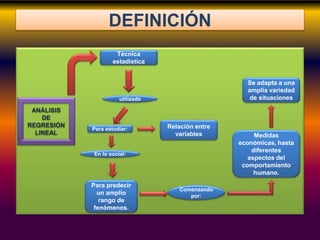
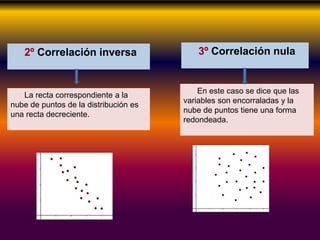
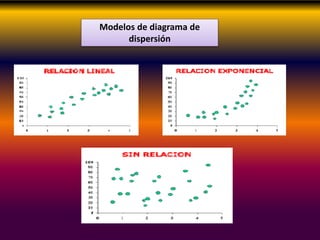
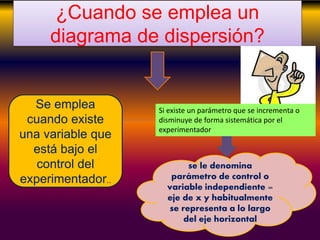
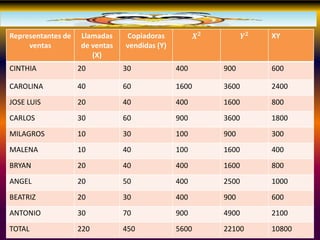
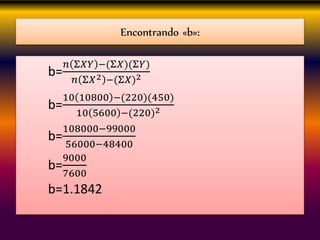
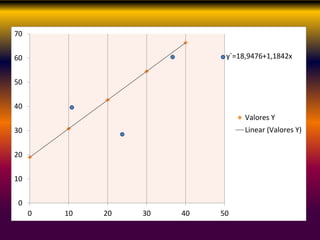
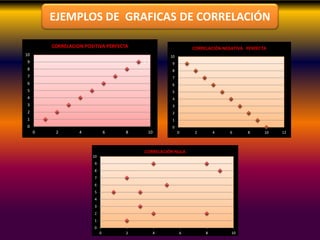
Este documento describe los conceptos clave de la regresión lineal, incluyendo su definición, tipos de regresión lineal, principios de mínimos cuadrados, gráficos de dispersión, y cómo se puede utilizar para predecir la relación entre variables. También explica cómo construir diagramas de dispersión y analizar los patrones de correlación para determinar si existe una relación lineal entre dos variables.

2. REGRESION
LINEAL

3. DEFINICIÓN
Técnica
estadística
ANÁLISIS
DE
REGRESIÓN
LINEAL
utilizada
Para estudiar: Relación entre
variables
En lo social:
Para predecir
un amplio
rango de
fenómenos.
Comenzando
por:
Medidas
económicas, hasta
diferentes
aspectos del
comportamiento
humano.
Se adapta a una
amplia variedad
de situaciones

4. En lo referente a la investigación de mercados:
Puede utilizarse
para :
Determinar en cual de
los diferentes medios
de comunicación es
mas eficaz intervenir.
o para predecir el
numero de ventas de un
determinado producto.

5. Clases de regresión lineal:
Clases de regresión
lineal:
Regresión lineal
simple
Regresión lineal
multiple

6. Regresión lineal simple:
• Este tipo se presenta cuando una variable independiente
ejerce influencia sobre otra variable dependiente. Ejemplo:
Y = f(x).
• Es una ecuación que define la relación lineal entre dos
variables donde una variable depende de la otra variable. Se
puede decir que Y depende de X.
Y = f(X)
Como Y depende de X, entonces:
Y es la variable dependiente, explicativa o
de predicción .
X es la variable independiente o variable
respuesta.

7. PRINCIPIO DE MINIMOS CUADRADOS
Técnica empleada para
obtener la ecuación de
regresión, minimizando la
suma de los cuadrados de las
distancias verticales entre los
valores verdaderos de Y y los
valores pronosticados de Y.

8. ¿QUÉ ES UN GRAFICO
DE DISPERSION?
Se trata de una representación
gráfica del grado de relación entre
dos variables cuantitativas

9. DIAGRAMA
S DE
DISPERSI
ON

10. INTRODUCCION:
Este documento describe el proceso completo a
seguir para analizar la existencia de una relación
lógica entre dos variables.
Describe la construcción de los Diagramas de
Dispersión a partir de la recogida de datos acerca
de dichas variables y el análisis posterior necesario
para confirmar la correlación que puede mostrar
dicho diagrama, ya que ésta no implica la
existencia de una relación lógica.

11. Es un tipo de diagrama matemático
que utiliza las coordenadas
cartesianas para mostrar los valores
de dos variables para un conjunto de
datos.
Los datos se muestran como un
conjunto de puntos, cada uno con el
valor de una variable que determina
la posición en el eje horizontal y el
valor de la otra variable determinado
por la posición en el eje vertical.
DIAGRAMA DE
DISPERSION:

12. CARACTERISTI
CAS
• IMPACTO VISUAL
Un Diagrama de Dispersión muestra la
posibilidad de la existencia de
correlación entre dos variables de un
vistazo.
• COMUNICACIÓN
Simplifica el análisis de situaciones
numéricas complejas.
• GUÍA EN LA INVESTIGACIÓN
El análisis de datos mediante esta
herramienta proporciona mayor
información
que el simple análisis matemático de
correlación, sugiriendo posibilidades y
alternativas de estudio, basadas en la
necesidad de conjugar datos y procesos
en su utilización.

13. NUBE DE PUNTOS O DIAGRAMA DE DISPERSIÓN.
Sobre la nube de
puntos puede trazarse
una recta que se ajuste
a ellos lo mejor posible,
llamada recta de
regresión.
1°Correlación directa
La recta correspondiente a la nube de
puntos de la distribución es una recta creciente.

14. 2º Correlación inversa
La recta correspondiente a la
nube de puntos de la distribución es
una recta decreciente.
3º Correlación nula
En este caso se dice que las
variables son encorraladas y la
nube de puntos tiene una forma
redondeada.

15. Llamado también ajuste de curvas es una ecuación dada en un grafico,
dependiendo del grado de correlación que mas se ajuste al conjunto
de datos.
AJUSTE LINEAL: Y=BX+A
AJUSTE LOGARITMICO: Y=B Ln X+A
AJUSTE EXPONENCIAL: Y=AC BX
AJUSTE PARABOLICO, CUADRATICO O POLINOMIAL: Y= AX2 + BX + A

16. Modelos de diagrama de
dispersión

17. El diagrama de dispersión es
una de las herramientas básicas
de control de calidad, que
incluyen además el histograma,
el diagrama de Pareto, la hoja
de verificación, los gráficos de
control el diagrama de flujo.
UN DIAGRAMA DE DISPERSIÓN
PUEDE SUGERIR VARIOS TIPOS DE
CORRELACIONES ENTRE LAS
VARIABLES CON UN INTERVALO DE
CONFIANZA DETERMINADO. LA
CORRELACIÓN PUEDE SER POSITIVA
(AUMENTO), NEGATIVA (DESCENSO),
O NULA (LAS VARIABLES NO ESTÁN
CORRELACIONADAS).

18. ¿Cómo elaborar un
diagrama de
dispersión?

19. QUE HACER PARA ELABORAR UN DIAGRAMA DE DISPERSIÓN:
1. Obtener tabla de pares de valores con valores
máximos y mínimos de cada variable.
2. Situar la causa sospechada en el eje horizontal.
3. Dibujar y rotular los ejes horizontales y verticales.
4. Trazar el área emparejada usando círculos
concéntricos en pares de datos idénticos.
5. Poner título al gráfico y rotular.
6. Identificar y clasificar el modelo de correlación.
7. Comprobar los posibles fallos en el análisis

20. ¿Cuando se emplea un
diagrama de dispersión?
Se emplea
cuando existe
una variable que
está bajo el
control del
experimentador..
Si existe un parámetro que se incrementa o
disminuye de forma sistemática por el
experimentador
se le denomina
parámetro de control o
variable independiente =
eje de x y habitualmente
se representa a lo largo
del eje horizontal

21. UN DIAGRAMA DE DISPERSION ME
REPRESENTARÁ
a) Una relación causal
 Solamente relaciones
b) Una explicación lógica para
establecer causa-efecto

22. LOS DIAGRAMAS DE DISPERSIÓN PUEDEN SER:
a. De Correlación Positiva
Se caracterizan porque al aumentar el valor de una variable
aumenta el de la otra.
b. De Correlación Negativa
Sucede justamente lo contrario, es decir, cuando una
variable aumenta, la otra disminuye.
c. De Correlación No Lineal.
No hay relación de dependencia entre las dos variables.

23. LINEA DE
TENDENCIA
Según sea la dispersión de
los datos (nube de puntos)
en el plano cartesiano,
pueden darse alguna de las
siguientes relaciones, Lineal,
Logarítmica, Exponencial,
Cuadrática, entre otras.

24. Primero: Elaborar una teoría admisible y relevante sobre la supuesta relación
entre dos variables.
Segundo: Recoger datos y construir el Diagrama.
Tercero: Identificar y clasificar la pauta de correlación.
Cuarto: Discutir la teoría original y considerar otras explicaciones.
La construcción y clasificación del Diagrama de Dispersión es la parte central
del proceso. No es ni el principio ni el final.
El análisis de un Diagrama de
Dispersión es un proceso de
cuatro pasos:

25. Ventajas y
desventajas
de los
diagramas de
dispersión

26. VENTAJAS DE LOS DIAGRAMAS
DE DISPERSION:
 Se trata de una herramienta especialmente útil
para estudiar e identificar las posibles relaciones
entre los cambios observados en dos
conjuntos diferentes de variables.
 Suministra los datos para confirmar hipótesis
acerca de si dos variables están relacionadas.
 Proporciona un medio visual para probar la
fuerza de una posible relación.
 Su utilización será beneficiosa para el desarrollo
de los proyectos abordados por los Equipos y
Grupos de Mejora y por todos aquellos
individuos u organismos w que estén implicados
en la mejora de la calidad.

27. DESVENTAJAS DEL DIAGRAMA
DE DISPERSIÓN:
No funciona si sucede que una dupla se repita
Solo se emplea cuando existe una variable que
esta bajo el control del experimentador.
Un diagrama de dispersión puede sugerir varios
tipos de correlaciones entre las variables .

28. CONCLUSIÓ
N
DIAGRAMA DE DISPERSION:
Su utilización será beneficiosa para el
desarrollo de los proyectos abordados por
los Equipos y Grupos de Mejora y por todos
aquellos individuos u organismos que
estén implicados en la mejora de la calidad.

29. FORMA GENERAL DE LA ECUACION DE
REGRESIÒN SIMPLE
Donde:
• Y’ se lee Y prima, es el valor pronosticado de la variable Y para un valor
seleccionador de X.
• «a» es la ordenada de la intersección con el eje Y, es decir, el valor estimado de Y
cuando X=0, es decir, donde la recta de regresión cruza el eje Y.
• «b» es la pendiente de la recta, o el cambio promedio en Y’ por unidad de
cambio en la variable independiente X.
• X es cualquier valor seleccionado de la variable independiente.
Y’=a+bx
En general, los valores de a y b en la ecuación de regresión
se denominan coeficientes de regresión estimados, o
también coeficientes de regresión.

30. Pendiente de la línea de regresión
b=
𝑛 Σ𝑋𝑌 −(Σ𝑋)(Σ𝑌)
𝑛 Σ𝑋2 −(Σ𝑋)2
Donde:
X es el valor de la variable independiente.
Y es el valor de la variable dependiente.
n es el numero de elementos en la muestra.

31. Para aplicar correctamente la regresión lineal
deben satisfacerse varias suposiciones:
Consideraciones básicas para la regresión
lineal:
1.-Para cada valor de la variable X
hay un conjunto de valores.
2.-Las desviaciones estándar de
todas estas distribuciones normales
son iguales.

32. 3.-Las medias de estas distribuciones
normales se encuentran sobre la
línea de regresión.
4.-Los valores de Y son
estadísticamente independientes.
Esto significa que al tomar la
muestra un determinado valor de X
no depende de ningún otro valor
de X. Esta suposición es
especialmente importante cuando
se toman los datos durante un
periodo.

33. CALCULOS NECESARIOS PARA DETERMINAR LA ECUACION DE
REGRESION DE MINIMOS CUADRADOS
EJEMPLO:
En la empresa Copier Sales of América, la gerente de ventas
recopilo información respecto al numero de llamadas telefónicas
hechas y la cantidad de copiadoras vendidas, para una muestra
de 10 representantes de ventas. A la señorita Madelei, gerente
de esa área, le gustaría ofrecer información especifica referente
a la relación entre el numero de llamadas y la cantidad de
productos vendidos. Utilice el método de mínimos cuadrados
para determinar la ecuación lineal.

34. Representantes de
ventas
Llamadas
de ventas
(X)
Copiadoras
vendidas (Y)
𝑿 𝟐
𝒀 𝟐 XY
CINTHIA 20 30 400 900 600
CAROLINA 40 60 1600 3600 2400
JOSE LUIS 20 40 400 1600 800
CARLOS 30 60 900 3600 1800
MILAGROS 10 30 100 900 300
MALENA 10 40 100 1600 400
BRYAN 20 40 400 1600 800
ANGEL 20 50 400 2500 1000
BEATRIZ 20 30 400 900 600
ANTONIO 30 70 900 4900 2100
TOTAL 220 450 5600 22100 10800

35. Encontrando «b»:
b=
𝑛 Σ𝑋𝑌 −(Σ𝑋)(Σ𝑌)
𝑛 Σ𝑋2 −(Σ𝑋)2
b=
10 10800 −(220)(450)
10 5600 −(220)2
b=
108000−99000
56000−48400
b=
9000
7600
b=1.1842

36. Luego «a»:
a=
Σ𝑌
𝑛
-b
Σ𝑋
𝑛
a=
450
10
− (1.1842)
220
10
a=45-(1.1842)22
a=18.9476
Por tanto, la ecuación de regresión es:
Y’=a+b(x)
Y’=18.9476+1.1842(X)

37. De modo que si un vendedor hace 20 llamadas telefónicas,
puede esperarse que venda :
Y’=18.9476+1.1842(X)
Y’=18.9476+1.1842(20)
Y’=42.6316
El valor b=1.1842 , significa que para
cada llamada adicional que realizan
los representantes de ventas pueden
esperar aumentar en casi 1.2 el
numero de copiadoras vendidas.

38. El valor a=18.9476 es el punto donde la ecuación
cruza el eje Y. Una traducción literal es que si no se
hacen llamadas, esto es, X=0, se venderán 18.9476
copiadoras. Obsérvese que X=0 se encuentra fuera
del intervalo de valores incluidos en la muestra, las
llamadas a clientes fueron de 10 a 40, así que los
cálculos deben hacerse dentro de esa gama de
valores.

39. 0
10
20
30
40
50
60
70
0 10 20 30 40 50
Valores Y
Linear (Valores Y)
y`=18,9476+1,1842x

40. El error de estándar de estimación sirve para mostrar la semejanza
que existe en concepto y calculo entre la desviación estándar y el
error estándar de estimación.
Supóngase que se estudia un gran número de observaciones y que
las cifras son grandes. Determine cada punto y’ sobre la recta de
regresión y elevar al cuadrado las DIFERENCIAS ESTO ES (Y-Y’),
SERIA MUY TEDIOSO. LA FORMULA QUE SIGUE ES IDENTICA
DESDE EL PUNTO DE VISTA ALGEBRAICO A LA ANTERIOR PERO ES
MUCHO MAS FACIL DE UTILIZAR.

41. FORMULA PARA EL ERROR
ESTANDAR DE ESTIMACION.
Al aplicar esta fórmula sale el mismo
resultado que se calculo antes. Se trata del
mismo error estándar de estimación.

42. Que describe la
intensidad entre dos
conjuntos
Es el estudio de relación que
existe entre las variables
dependientes e
independientes.
COEFICIENTE DE CORRELACIÓN

43. VARIABLE DEPENDIENTE (Y) VARIABLES INDEPENDIENTES (X1, X2,......)
VOLUMEN DE VENTAS, EN UNIDADES Precio unitario
Gasto de Propaganda
PESO DE LOS ESTUDIANTES Estatura
Edad
CONSUMO DE BIENES INDUSTRIALES POR
AÑO
Ingreso disponible
Importación de bienes de consumo
UNIDADES CONSUMIDAS DE UN BIEN POR
FAMILIA
Precio unitario del bien
Ingreso
Número de integrantes por familia
PRECIO DE UNA VIVIENDA
Nº de habitaciones
Nº de pisos
Área construida
Área techada , etc.
EJEMPLOS

44. Nuestro principal objetivo al
analizar las dos variables X y Y,
para poder determinar la
relación entre éstas dos
variables, es decir como se
comportan las dos variables
una con respecto a la otra

45. COEFICIENTE DE
CORRELACIÓN
El Coeficiente de Correlación (r):
requiere variables medidas en escala de intervalos
o de proporción, que Varía entre -1 y 1.
• Valores de -1 ó 1 indican correlación
perfecta.
• Valor igual a 0 indica ausencia de
correlación.
• Valores negativos indican una relación lineal
inversa
• valores positivos indican una relación lineal
directa

46. EJEMPLOS DE GRAFICAS DE CORRELACIÓN
0
1
2
3
4
5
6
7
8
9
10
0 2 4 6 8 10 12
CORRELACIÓN NEGATIVA PERFECTA
0
1
2
3
4
5
6
7
8
9
10
0 2 4 6 8 10
CORRELACIÓN NULA
9, 9
0
1
2
3
4
5
6
7
8
9
10
0 2 4 6 8 10
CORRELACION POSITIVA PERFECTA

47.       2222
Σ-Σ)Σ()Σ(
)Σ)(Σ()Σ(
YYnXXn
YXXYn
R



LÍNEA RECTA y= a+bx
CALCULA EL COEFICIENTE DE CORRELACIÓN “R” SIN UTILIZAR MEDIAS
ARITMÉTICAS DE LAS VARIABLES
MODELOS
FORMULAS QUE NOS PERMITEN HALLAR EL COEFICIENTE DE
CORRELACIÓN “R” DE PEARSON

48. TAMBIÉN SE PUEDE CALCULA EL COEFICIENTE DE CORRELACIÓN “R”
UTILIZANDO LAS MEDIAS ARITMÉTICAS DE LAS VARIABLES
  22
)()(
))((





yyxx
yyxx
R
n = es el número de pares de observaciones.
∑X = es la suma de los valores de la variable X.
∑Y = es la suma de los valores de la variable Y.
(∑X2) = es la suma de los cuadrados de los valores de la variable X.
(∑X)2 = es el cuadrado de la suma de los valores de la variable X.
(∑Y2) = es la suma de los cuadrados de los valores de la variable Y.
(∑Y)2 =es el cuadrado de la suma de los valores de la variable Y.
∑XY = suma de los productos de X y Y.

49. LÍNEA RECTA y= a + bx
CALCULA EL COEFICIENTE DE CORRELACIÓN “R” SIN UTILIZAR MEDIAS
ARITMÉTICAS DE LAS VARIABLES
      2222
Σ-Σ)Σ()Σ(
)Σ)(Σ()Σ(
YYnXXn
YXXYn
R



R=
10 10800 − 200 (450)
10(5600)− 200 2 10 22100 − 450 2
R= 0.759

50. ¡Gracias!