Descargado 24 veces
Subido porTensor
Regresion lineal
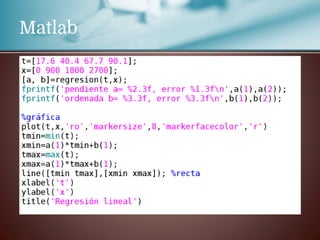
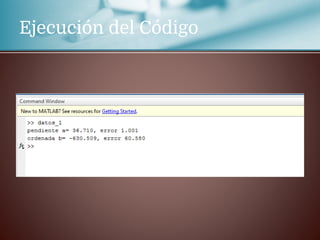
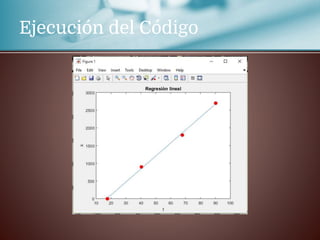
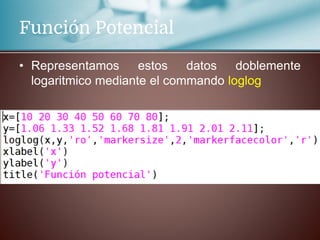
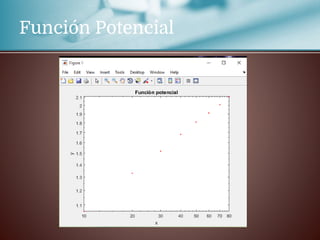
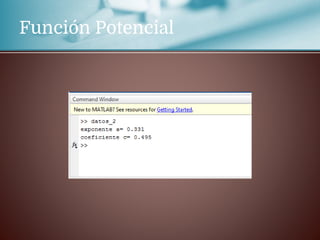
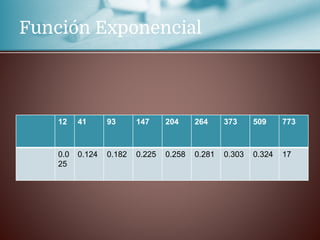
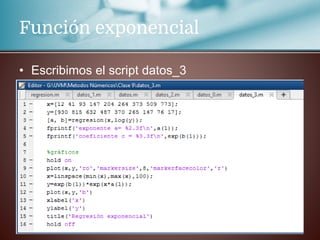
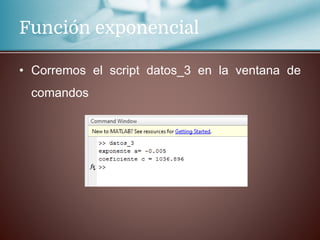
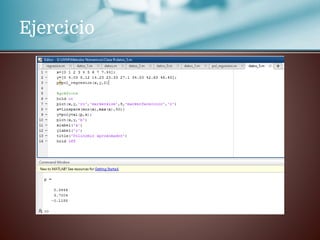
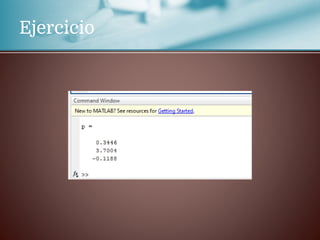
Este documento trata sobre la regresión lineal. Explica que se estudiará el método de mínimos cuadrados para aproximar un polinomio a un conjunto de datos experimentales. Aborda las distribuciones bidimensionales donde se disponen los datos experimentales en dos columnas con la abscisa x y su ordenada y para investigar cómo una variable influye en la otra. Como ejemplo, menciona que la cantidad de lluvia puede dar lugar a un aumento de la producción agrícola.
Más contenido relacionado
Regresion lineal
- 1.
- 2. Regresión Lineal • Estudiaremosla regresión lineal, es decir la determinación de la ecuación de la recta que mejor ajusta a una distribución bidimensional de datos. Se explicará el método de los mínimos cuadrados para aproximar un polinomio a un conjunto de datos experimentales.
- 3. Regresión Lineal • Abordaremoslas distribuciones bidimensionales. Las observaciones se dispondrán en dos columnas, de modo que en cada fila figuren la abscisa x y su correspondiente ordenada y. La importancia de las distribuciones bidimensionales radica en investigar como influye una variable sobre la otra.
- 4. Regresión Lineal • Estapuede ser una dependencia causa efecto, por ejemplo, la cantidad de lluvia (causa), da lugar a un aumento de la producción agrícola (efecto). O bien, el aumento del precio de un bien, da lugar a una disminución de la cantidad demandada del mismo.
- 5. Regresión Lineal • Siutilizamos un sistema de coordenadas cartesianas para representar la distribución bidimensional, obtendremos un conjunto de puntos conocido con el diagrama de dispersión, cuyo análisis permite estudiar cualitativamente, la relación entre ambas variables.
- 6.
- 7.
- 8.
- 9.
- 10. Regresión Lineal • Elextremos de una función: máximo o mínimo se obtiene cuando las derivadas de E respecto de a y de b sean nulas. Lo que da lugar a un sistema de dos ecuaciones con dos incógnitas del que se despeja a y b.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18. Ejercicio Práctico 17.6 0 40.4900 67.7 1800 90.1 2700
- 19.
- 20.
- 21. Funciones y Códigoen Matlab
- 22.
- 23.
- 24.
- 25. Ejecución del Código •En la ventana de comandos corremos el script datos_1.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31. Función Potencial 10 2030 40 50 60 70 80 1.06 1.33 1.52 1.68 1.81 1.91 2.01 2.11
- 32. Función Potencial • Representamosestos datos doblemente logaritmico mediante el commando loglog
- 33.
- 34. Función Potencial • Paradeterminar la recta de regresión, se transforma esta tabla de datos en esta otra 1.0 1.30 1.477 1.60 1.699 1.778 1.845 1.903 0.0 25 0.124 0.182 0.225 0.258 0.281 0.303 0.324
- 35. Función Potencial • Calculamosmediante la función regresión los parámetros a y c. • Escribimos el script datos_2 y lo corremos el script datos_2 en la ventana de comandos
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42. Función Exponencial 12 4193 147 204 264 373 509 773 0.0 25 0.124 0.182 0.225 0.258 0.281 0.303 0.324 17
- 43. Función exponencial • Representamosestos datos en un diagrama semilogarítmico mediante el comando semilogy
- 44.
- 45.
- 46. Función Exponencial • Paradeterminar la recta de regresión, se transforma esta tabla de datos en esta otra 12 41 93 147 204 264 373 509 773 6.8 35 6.703 6.449 6.188 5.913 5.580 4.990 4.330 2.833
- 47. Función exponencial • Escribimosel script datos_3
- 48. Función exponencial • Corremosel script datos_3 en la ventana de comandos
- 49. Función exponencial • Corremosel script datos_3 en la ventana de comandos
- 50.
- 51.
- 52.
- 53. Polinomio aproximador • Secalcula la cantidad
- 54.
- 55.
- 56.
- 57. Polinomio aproximador • quepodemos escribir, alternativamente
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.