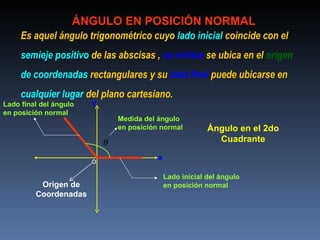
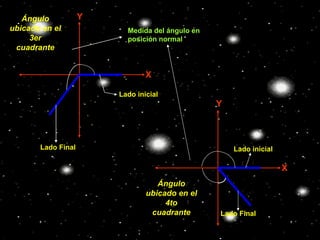
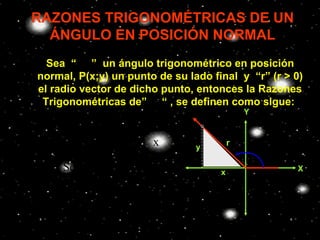
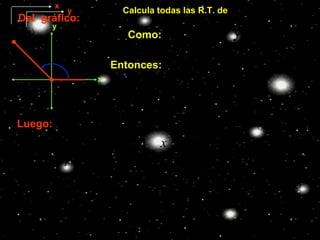
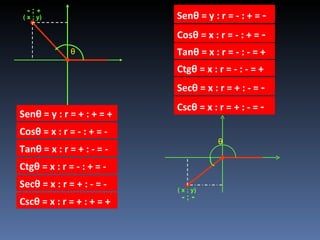
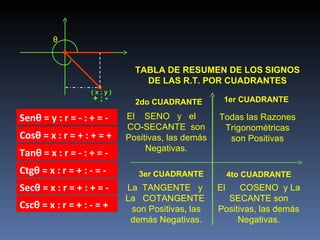
Este documento describe los ángulos en posición normal y sus razones trigonométricas. Define un ángulo en posición normal como uno cuyo lado inicial coincide con el eje positivo de las abscisas y cuyo vértice está en el origen. Explica cómo calcular las seis razones trigonométricas de un ángulo en posición normal y muestra ejemplos numéricos. También resume los signos de las razones trigonométricas en los cuatro cuadrantes.

1. Trigonometría
Moderna
ÁNGULOS EN POSICIÓN NORMAL
Y SUS
RAZONES TRIGONOMETRICAS
PROFESOR
Pedro Asencios Villavicencio
pedroasencios@gmail.com

2. ÁNGULO EN POSICIÓN NORMAL
Es aquel ángulo trigonométrico cuyo lado inicial coincide con el
semieje positivo de las abscisas , su vértice se ubica en el origen
de coordenadas rectangulares y su lado final puede ubicarse en
cualquier lugar del plano cartesiano.
Lado final del ángulo Y
en posición normal
Medida del ángulo
en posición normal Ángulo en el 2do
θ Cuadrante
o x
Lado inicial del ángulo
Origen de en posición normal
Coordenadas

3. Ángulo Y
ubicado en el Medida del ángulo en
3er posición normal
cuadrante
θ
X
Lado inicial
Y
Lado Final Lado inicial
X
θ
Ángulo
ubicado en el
4to
cuadrante Lado Final

4. RAZONES TRIGONOMÉTRICAS DE UN
ÁNGULO EN POSICIÓN NORMAL
Sea “ θ ” un ángulo trigonométrico en posición
normal, P(x;y) un punto de su lado final y “r” (r > 0)
el radio vector de dicho punto, entonces la Razones
Trigonométricas de” θ “ , se definen como sigue:
Y
P( x; y )
y x y
Senθ = Cosθ = Tanθ =
r r x y
r θ
x r r
Ctgθ = Sec θ = Csc θ = x X
y x y

5. Calcula todas las R.T. de θ
x
y
Del gráfico:
( − 5 ;12)
y
Como: r =x +y
2 2 2
θ
r = ( − 5) + (12)
2 2 2
Entonces:
x
∴ r = 13
Luego:
y 12 x −5 y 12
Senθ = = Cosθ = = Tanθ = =
r 13 r 13 x −5
r 13 y 13 x −5
Cscθ = = Secθ = = Ctgθ = =
y 12 x −5 y 12

6. 2) Calcula: Secθ − Cscθ en:
-2
-1
θ
r= θ
( − 2) 2 + ( − 1) 2 = r 2
Resolución.-
Lo primero será calcular el valor del radio r
vector
Entonces: x = −2 ; y = −1; r = 5
Luego:
Secθ − Cscθ = r r
+
x y = 5
+
- 2 -1
5
Secθ − Cscθ = − 5 −2 5
2
+
2
= −3 5
2

7. En el gráfico:
θ ( 4 ; 5)
( -4 ; -5)
Calcula: Senφ − Secφ
Resolución.-
Trasladamos el punto (4;5) por simetría, asiendo rotaciones de 90°.
Luego: 21 21
Senφ − Secφ = 41 − − 4 = −4 41 = 4 41
−5 41
−

8. SIGNOS DE LAS RAZONES TRIGONOMÉTRICAS
Como las razones trignométricas dependen de dos cantidades
(abscisas, ordenadas y/o radio vector), nos percatamos que las
razones trigonométricas tienen un signo que se obtiene de la
combinación de los signos que poseen estas cantidades.
+;+
( x ; y) Senθ = y : r = + : + = +
Cosθ = x : r = + : + = +
θ Tanθ = x : r = + : + = +
Ctgθ = x : r = + : + = +
Secθ = x : r = + : + = +
Cscθ = x : r = + : + = +

9. -;+
( x ; y) Senθ = y : r = - : + = -
Cosθ = x : r = - : + = -
θ Tanθ = x : r = - : - = +
Ctgθ = x : r = - : - = +
Secθ = x : r = + : - = -
Cscθ = x : r = + : - = -
Senθ = y : r = + : + = +
Cosθ = x : r = - : + = -
θ
Tanθ = x : r = + : - = -
Ctgθ = x : r = - : + = -
Secθ = x : r = + : - = - ( x ; y)
-;-
Cscθ = x : r = + : + = +

10. θ
TABLA DE RESUMEN DE LOS SIGNOS
DE LAS R.T. POR CUADRANTES
(x;y)
+;- 2do CUADRANTE 1er CUADRANTE
Senθ = y : r = - : + = - El SENO y el Todas las Razones
CO-SECANTE son Trigonométricas
Cosθ = x : r = + : + = + Positivas, las demás son Positivas
Negativas.
Tanθ = x : r = - : + = -
Ctgθ = x : r = + : - = - 3er CUADRANTE 4to CUADRANTE
Secθ = x : r = + : + = - La TANGENTE y El COSENO y La
La COTANGENTE SECANTE son
Cscθ = x : r = + : - = + son Positivas, las Positivas, las demás
demás Negativas. Negativas.