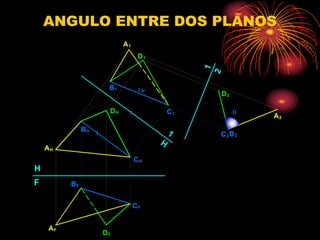
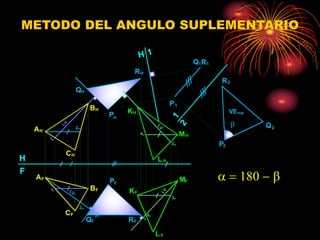
Este documento describe varios métodos para calcular los ángulos entre rectas y planos. Explica cómo calcular el ángulo entre dos rectas que se cruzan proyectándolas en su longitud verdadera. También cubre cómo calcular el ángulo entre una recta y un plano, ya sea usando el método del plano o el de la recta. Por último, detalla métodos como el de los planos de canto o el del ángulo suplementario para hallar el ángulo entre dos planos.

2. ANGULO ENTRE RECTAS
• Rectas que se intersectan
• Rectas que se cruzan
• ANGULOS ENTRE PLANOS
• Planos que se intersectan
• Planos que se cruzan
CAPITULO VII
ANGULOS

3. INTRODUCCION
• Muchos veces en el campo de la
ingeniería se presentan problemas de
cómo hallar el ángulo que forman dos
elementos estructurales que se
cruzan o se intersectan

4. DEFINICION:
Es el conjunto de puntos entre dos
rectas: angulo plano
Es el conjunto de puntos entre dos
planos: angulo diedro

5. ÁNGULO ENTRE DOS RECTAS QUE
SE CRUZAN
En el espacio, el ángulo entre dos rectas
que se cruzan queda definido mediante el
ángulo menor de los ángulos adyacentes,
se observará en verdadera amplitud (VA),
en la vista en donde las dos rectas se
proyectan en verdadera longitud(VL).

6. ANGULO ENTRE DOS RECTAS QUE SE
CRUZAN
K
L
A
B

7. ANGULO ENTRE DOS RECTAS
QUE SE CRUZAN

K
L
L' L''
K''
A
K'
V
U
B

8. METODO 1: PROYECTANDO AMBAS
RECTAS EN LV
• Determinamos una de las rectas, como un
punto, en una vista auxiliar y luego con una
nueva línea de pliegue paralela a la otra
recta, se obtiene en esta nueva vista las
longitudes verdaderas (LV) de ambas, y por
consiguiente el ángulo que forman en
verdadera amplitud.
• En el depurado en la proyeccion 1 la recta
AB de punta y en la vista 2 ambas rectas en
sus longitudes verdaderas de las rectas AB
y RS y por lo tanto el ángulo en verdadera
amplitud

9. METODO 1 RECTAS EN LONGITUD
VERDADERA
AH
H
F
BH
RH
SH
RF
AH BF
SF
LV
H 1
S1
R1
A1 B1
1
2
B2
A2
S2
R2

LV
LV


10. METODO 2: De la recta paralela y la
formación de un plano.
• En el depurado, por la recta AB
trazamos una paralela a CD, tal como
BF, determinando el plano ABF que
proyectamos en VE en la vista 2,
donde el ángulo ABF que se proyecta
en verdadera amplitud es el ángulo
que forma la recta AB con la recta CD

11. METODO 2 FORMACION DE UN PLANO
H
F
AH
BH
CH
DH
AF
BF
DF
CF
FH
FF
LV
1H
1F
H
1
1
2
B1
A1
F1
11
C1
D1
D2
C2
B2
F2
A2
L
V
LV
12
LV


12. ÁNGULO ENTRE UNA RECTA Y UN
PLANO
Siempre que una recta no esté
contenida en un plano, el ángulo
formado por esta recta con su
proyección sobre el plano es el ángulo
entre la recta y el plano.
El ángulo entre la recta y el plano se
mostrará en su verdadera amplitud en
la vista donde el plano se proyecte de
canto y la recta en verdadera
longitud(VL)
•

13. ANGULO ENTRE UNA RECTA Y UN PLANO
A
L
B
A'
C


14. MÉTODO 1: METODO DEL PLANO
Dadas las proyecciones H y F de un
plano y una recta.
En la primera vista, proyectamos al
plano de canto y a la recta en
posición cualesquiera.
En la segunda, el plano en VE y la recta
en cualquier posición.
En la tercera, el plano de canto y la
recta en VL, obteniéndose el ángulo
entre la recta y el plano de canto.

15. METODO DEL PLANO
H
AH
H
F
BH
CH
AF
BF
CF
YF
XF
XH
YH
B1
A1
C1
X1
Y1
B2
A2
C2
X2
Y2
Y3
X3
A3
C3
B3

1
1
2
2
3
1H
1F
LV


16. MÉTODO 2: METODO DE LA RECTA
Dada las proyecciones del plano y la
recta, hallar el ángulo entre la recta y
el plano
• -En la primera, proyectamos la recta
VL y el plano en cualquier posición.
• - La segunda vista, la recta como
punto y el plano en VE.
• - En la tercera vista la recta en VL y el
plano del canto; entonces podremos
medir la verdadera eamplitud del
ángulo entre el plano y la recta.

17. METODO DE LA RECTA
H
RH
11
12
LV
AH
BH
CH SH
SF
RF
AF
CF
BF
F
1
1
2
A1
B1
C1
R1
S1
B2
A2
C2
S2R2
B3
C3
A3
S3
R3
LV
H
2
3


18. MÉTODO 3. METODO DEL ANGULO
COMPLEMENTARIO
• En esquema se observa la recta MN y
el plano ABC forman un ángulo , que
viene a ser el ángulo entre la recta y
el plano.
• Trazamos una perpendicular de la
recta MN al plano, determinamos un
plano MRN, donde el ángulo  es el
complemento del ángulo , por lo
tanto  = 90º - 

19. METODO DEL ANGULO
COMPLEMENTARIO

X
Y


M Z
R N
B
A
C

20. • Se dan las proyecciones del plano ABC y la recta
MN, determinaremos el ángulo.
• Desde el punto M de MN, trazamos una
perpendicular al plano, hasta un punto R formando
el plano MNR. Prescindiendo del plano ABC,
determinamos la VE del plano MNR, en la vista 2,
en donde observamos recta MN y MR formando el
ángulo entre ellos, que es el valor del ángulo
complementario .
•
• En la vista 2, por M trazamos una línea
perpendicular a MN, determinando la amplitud del
ángulo , que es el complemento de del ángulo .
PROCEDIMIENTO

21. METODO DEL ANGULO
COMPLEMENTARIO
H
F
1
AH
BH
CH
NH
MH
CF
BF
MF
L
V
1F
1H
2F
2H
LV
NF
RH
M1
N 1
R1
R2
N 2
M2
LV
1
2


H
AF
NF

22. ÁNGULO ENTRE DOS PLANOS
Dos planos que se cortan forman 4 ángulos
diedros
CASO 1: CUANDO SE CONOCE LA RECTA DE
INTERSECCION
Dado los planos ABC Y BCD, para hallar el ángulo
entre dichos planos, identificamos primero la
recta de intersección BC, luego proyectamos en
LV esta recta en la vista 1 y de punta en la vista
2; en esta vista los dos planos propuestos se
proyectan de canto, y podremos medir el ángulo
entre ambos planos.

23. ANGULO ENTRE DOS PLANOS

P
F B
K
L
A
E
G
I
M
N

PLANO P PERPENDICULAR A LA RECTA AB
INTERSECCION DE LOS PLANOS MNKL y EFGI
P
EF
IG
LK
MN
AB
PLANO P EN VERDADERA EXTENCION(VE)

24. ANGULO ENTRE DOS PLANOS

H
H
1
AH
F
BH
DH
CH
CF
DF
AF
BF
C1
B1
D2
C2B2
A2
D1
A1
LV
1
2

25. Caso 2: CUANDO O SE CONOCE LA
LÍNEA DE INTERSECCION
MÉTODO 1: DE LOS PLANOS DE CANTO
En la vista 1, disponemos uno de los planos
de canto y el otro en posición cualquiera.
En la vista adyacente proyectamos el primer
plano en VE y en el otro plano una recta en
LV contenido en dicho plano.
En la vista 3 (ponemos la línea de pliegue 2-
3 perpendicular a la recta en LV del 2do .
plano), ambos planos se proyectarán de
canto y podremos medir el ángulo entre
ambos planos.

26. METODO DE LOS PLANOS DE CANTO
1
2
3

H
H
1
2
AH
DH
F
CH
BH
FH
EH
AF
CF
BF
DF
EF
FF
1H
1F
LV
11
A1
C1
B1
EH
D1
F1
21
22
C2
A2
B2
E2
D2
F2
LV
F3
E3
D3
B3
A3 C3
23

27. METODO 2: DEL ANGULO
SUPLEMENTARIO
Por el punto P trazamos PQ Y PR
perpendiculares a los planos ABC y K LM,
obteniéndose el plano PQR, que lo
proyectamos primero de canto y luego en
VE en la vista 2, en esta vista se observa el
ángulo , que forma RP con QP, en su
verdadera amplitud; que es el suplemento
de del ángulo que buscamos: 180- = 

28. ANGULO ENTRE DOS PLANOS
METODO: ANGULO SUPLEMENTARIO
Q
P
Y
R
X
RECTA DE INTERSECCION DE LOS PLANOS ABC Y KLMN
L
M
N
K
B
A
D
C




29. METODO DEL ANGULO SUPLEMENTARIO
H
1H
2H
2H
1F
MH
KH
LH
L F
MF
KF
3H
4H
3F
4F
PF
QH
RH
PH
QF RF
Q1R1
P1
R2
Q2
P2
VEPQR
1
2
L
V
LV
L
V
L
V


H
F
H
1
AH
BH
AF
CF
BF
C