Incrustar presentación
Descargar como PPS, PPTX

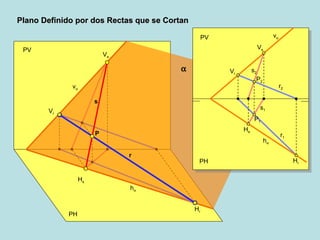
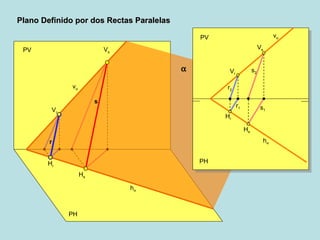
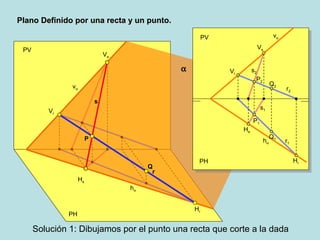
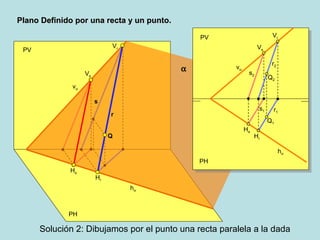
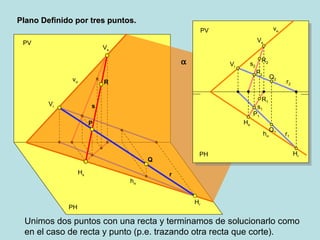
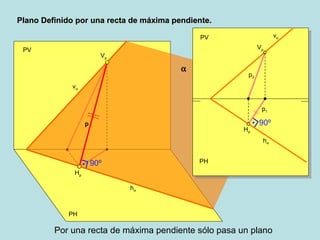
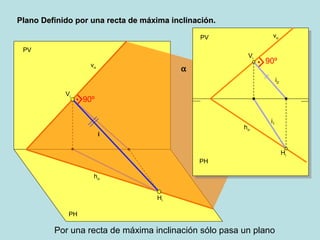
Este documento describe diferentes métodos para definir un plano geométrico, incluyendo: (1) dos rectas que se cortan, (2) dos rectas paralelas, (3) una recta y un punto, (4) tres puntos, (5) una recta de máxima pendiente, y (6) una recta de máxima inclinación. Explica gráficamente cada método a través de diagramas.







