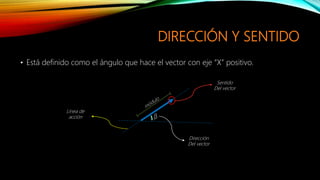
El documento presenta los objetivos y conceptos básicos del análisis vectorial. Explica que un vector es una expresión matemática con orientación que se representa gráficamente como un segmento de recta dirigido. Define las propiedades de los vectores como su módulo, dirección y sentido, y que dos vectores son iguales si comparten estas características. También cubre la propiedad de que dos vectores son coloniales si uno es un múltiplo escalar del otro.

1. ANÁLISIS
VECTORIAL
Prof. Einstein Vásquez

2. OBJETIVOS DE LA CLASE:
Al final de la sesión el alumno estará en la capacidad de:
• Reconocer y utilizar el vector y sus propiedades.
• Aplicar las propiedades de los vectores en problemas
aplicativos.

3. VECTOR
• Expresión matemática con cierta orientación representando gráficamente
mediante un segmento de recta dirigida.
Sentido
Del vector
Línea de
acción

4. MÓDULO
• Es la magnitud o tamaño del vector.
Ejemplo

5. DIRECCIÓN Y SENTIDO
• Está definido como el ángulo que hace el vector con eje “X” positivo.
Sentido
Del vector
Línea de
acción β
Dirección
Del vector

6. PROPIEDADES
Dos o más vectores son iguales si poseen igual módulo, dirección y sentido.
d
d A C
B
B CA

7.  Dos vectores son coloniales si existe un número real que al multiplicarse por uno de
ellos nos da el otro vector.
Sean los vectores A y B, estos vectores serán coloniales si y solo si:
A = n.B , donde “n” Є R
Esto significa que si:
n > 0 los vectores además son paralelos.
n < 0 los vectores además son anti paralelos.
C
A B
A, B y C son vectores coloniales,
mientras que:
 A y B : Son vectores paralelos
 A y C : Son vectores anti paralelos.

8. BIBLIOGRAFÍA
• https://es.slideshare.net/Humbertoech/analisis-vectorial-8332045
• https://es.slideshare.net/jorgesia56/anlisis-vectorial-13742857
VIDEOS RELACIONADOS:
• https://www.youtube.com/watch?v=8oVmHEoWZ6s&t=642s