Resumen aplicaciones derivadas bachillerato

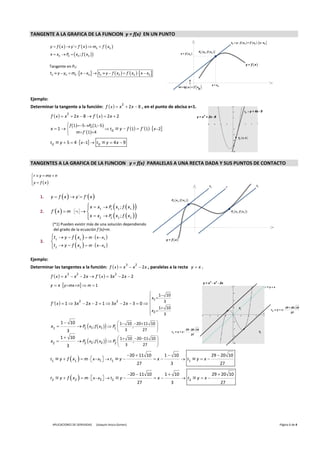
1. TANGENTE A LA GRAFICA DE LA FUNCION y = f(x) EN UN PUNTO
t0  y ‐ f  x0  = f´  x0    x ‐ x0 
y  f  x   y´ f ´ x   m0  f ´ x0 
P0  x0 ; f  x0  
x  x0  P0   x0 ; f  x0  
x = f  x0 
y = f x
Tangente en P0:
t0  y  y0  m0   x  x0   t0  y  f  x0   f ´ x0    x  x0 


m = tg   = f´ x  0 x = x0
Ejemplo:
Determinar la tangente a la función: f  x   x  2 x  8 , en el punto de abcisa x=1.
2
t0  y = 4x ‐ 9
f  x   x  2 x  8  f ´ x   2 x  2
2
y = x 2 + 2x ‐ 8
 f 15P0 1;5 

x 1  t0  y  f 1  f ´1   x 2

 m  f ´14
P0  1;‐5 
t0  y  5  4   x 1  t0  y  4x  9
TANGENTES A LA GRAFICA DE LA FUNCION y = f(x) PARALELAS A UNA RECTA DADA Y SUS PUNTOS DE CONTACTO
r  y  mx  n


y  f  x 
 t2 t1
r
1. y  f  x   y ´ f ´ x 
P2  x 2 ; f  x 2  
 x  x1  P1  x1 ; f  x1  

2. f ´ x   m *1   P1  x1 ; f  x1  
 x  x2  P2  x2 ; f  x2  
 

[*1} Pueden existir más de una solución dependiendo
del grado de la ecuación f´(x)=m.
t1  y  f  x1   m   x  x1  y = f x
3. 
t2  y  f  x2   m   x  x2 
Ejemplo:
Determinar las tangentes a la función: f  x   x  x  2 x , paralelas a la recta y  x .
3 2
f  x   x  x  2 x  f ´ x   3 x  2 x  2
3 2 2
y  x  y mx  n  m  1
y = x 3 ‐ x 2 ‐ 2x
r y=x
 1 10
 x1 

f ´ x   1  3 x  2 x  2  1  3 x  2 x  3  0   3
2 2
 1 10 P1
y= x‐
29 + 20 10
 x2  3
t2
 27
1  10  1 10 20 11 10 
x1   P1  x1 ; f  x1    P1  ; 
3  3 27  t1 y= x‐
29 ‐ 20 10 P2
27
1  10  1 10 20 11 10 
x2   P2  x2 ; f  x2    P2  ; 
3  3 27 
20  11 10 1  10 29  20 10
t1  y  f  x1   m   x  x1   t1  y 
  x  t1 yx
27 3 27
20  11 10 1  10 29  20 10
t2  y  f  x2   m   x  x2   t2  y 
  x  t2 yx
27 3 27
APLICACIONES DE DERIVADAS (Joaquín Aroca Gomez) Página 1 de 4

2. EXTREMOS RELATIVOS DE LA FUNCION y = f(x) [MAXIMOS Y MINIMOS, CRECIMIENTO DECRECIMIENTO]
y = f x
 
f ´ x0   0  DECRECIENTE
 
f ´ x0   0  CRECIENTE P0  x0 ; f  x0   t0  y = f  x 0 
t0  y = f  x 0   
f ´ x0   0  DECRECIENTE
P0  x0 ; f  x0  
 
f ´ x0   0  CRECIENTE
x0  x0  x0  x0 
x0 x0
MINIMO
MAXIMO y = f x
y´ f ´ x 
1. y  f  x  
y´´ f ´´ x 
 x  x1
x  x

2. f ´ x   0  
RESOLVIENDO LA ECUACION
 2
  x  xi POSIBLES EXTREMOS 
 
 ....
 x  xn

 
 f ´ x i   0  f ´ xi   0 
 

3. x  xi  MINIMO   MAXIMO   
  f ´´ xi   0  f ´´ x i   0 
   
  f ´n  xi   0  MINIMO

Si la primera derivada no nula es par   ´n
NOTA: Cuando f ´´ x i   0    f  xi   0  MAXIMO


 Si la primera derivada no nula es impar  PUNTO DE INFLEXION.


 f ´ xi   0

 f ´ xi   0 
 
   
   
Tambien podemos aplicar : x  x i  MINIMO   f ´ x i   0 MAXIMO   f ´ xi   0 
   

 

 f ´ xi  0

 f ´ xi  0 
 
   
Ejemplo 1:
Determinar los máximos, mínimos y monotonía de la función: f  x   2 x  9 x  12 x .
3 2
 f ´ x 6 x 2 18 x 12

f  x   2 x  9 x  12 x  
3 2
1.

 f ´´ x 12 x 18
2. f ´ x   0  6 x  18 x  12  0 
2
 x1  1
x2  2
 f ´1  0
x  x 1  1    P1  x1 ; f  x1    1; 5  MAXIMO
 f ´´1  6  0 P1  1; 5  MAXIMO
3.
 f ´2  0
x  x 2  2    P2  x 2 ; f  x 2     2; 4  MINIMO
 f ´´2   6  0 P2  2; 4  MINIMO
 f ´1   f ´ 0, 9   0, 66  0

x  x 1  1   f ´1  0  P1  x1 ; f  x1    1; 5 MAXIMO
 f ´1   f ´1,1  0, 54  0

 f ´2   f ´1, 9   0, 54  0

x  x 2  2   f ´2   0  P2  x2 ; f  x2     2; 4  MINIMO x1 = 1 x2 = 2
 f ´2   f ´2,1  0, 66  0


MONOTONIA (CRECIMIENTO DECRECIMIENTO)
x  ;1 x 1 x  1;2  x 2 x   2; 
CRECIENTE  x    ;1   2; 
f ´ x   6 x 18 x 12  f ´ x   0 f ´ x   0 f ´ x   0 f ´ x   0 f ´ x   0
2
DECRECIENTE  x  1;2 
y  f  x   3 x  9 x  12 x 
3 2
CRECIENTE MAXIMO DECRECIENTE MINIMO CRECIENTE
APLICACIONES DE DERIVADAS (Joaquín Aroca Gomez) Página 2 de 4

3. Ejemplo 2:
3
x
Determinar los máximos y mínimos de la función: f  x   .
x 1
 3 x 2  x 1 x 3 2 x 3 3 x 2
 f ´ x  
 x 1  x 12

1. f x 
x
3


  f ´´ x 
2
 

6 x 2 12 x  x 1 2 2 x 3 6 x 2  x 1 2 x 3 6 x 2 6 x
 
x 1   x 14  x 13

 24
 f ´´´ x 

  x 15
 x1  0

f ´ x   0  2 x  3 x  0  
3 2
2. 3
 x2  2
  3 27 
P2  ;  MINIMO
2 4 
 f ´ 0   0

x  x 1  0  

f ´´ 0 0

 f ´´ 0   0  f ´´´ 0 24  0 Primera derivada no nula impar 

3
 P1  x1 ; f  x1     0; 0  PUNTO DE INFLEXION
P1  0; 0  P. INFLEXION x2 =
2
3.

x1 = 0
 f´ 3  0

 P2  x 2 ; f  x 2     ;  MINIMO
3 2  3 27 
x  x 2   
2 3
 f ´´ 2  18  0
  2 4 
MONOTONIA (CRECIMIENTO DECRECIMIENTO)
 3 3 
x    ;0 
3
x0 x   0;  x x   ; 
 2 2 2 
f ´ x   0 3 
CRECIENTE  x   ; 
2 
f ´ x   6 x 18 x 12
2
f ´ x   0 f ´´ x   0 f ´ x   0 f ´ x   0 f ´ x   0
 3
DECRECIENTE  x    ;0    0; 
f ´´´ x   0  2
PUNTO DE
y  f  x   3 x  9 x  12 x 
3 2
DECRECIENTE DECRECIENTE MINIMO CRECIENTE
INFLEXION
PUNTOS DE INFLEXION DE LA FUNCION y = f(x) [CURVATURA]
y = f x t0
y = f x
P0  x0 ; f  x0  
 
f ´ x0   0  CRECIENTE
 
f ´ x0   0  DECRECIENTE
P0  x0 ; f  x0  
t0
f ´ x0    0  DECRECIENTE

 f´´  x0   0
 
f ´ x0   0  CRECIENTE 

x0  x0  x0  x0   f´´´  x0   0

x0  f´´  x0   0
 x0

P. INFLEXION  f´´´  x0   0

P. INFLEXION
t0 t0
P0  x0 ; f  x0   P0  x0 ; f  x0  
f´´  x0   0 f´´  x0   0
y = f x
y = f x
x0 x0
CONCAVA HACIA ARRIBA   
  CONCAVA HACIA ABAJO   
 
APLICACIONES DE DERIVADAS (Joaquín Aroca Gomez) Página 3 de 4

4.  y´ f ´ x 

1. y  f  x    y´´ f ´´ x 
y´´´ f ´´´ x 

 x  x1
x  x

2. f ´´ x   0  
 2
  x  xi POSIBLES PUNTOS DE INFLEXION 
RESOLVIENDO LA ECUACION
 
 ....
 x  xn

 f ´´ x i   0

3. x  xi  PUNTO DE INFLEXION  
 f ´´´ x i   0

NOTA: Cuando f ´´ x i   0  Si la primera derivada no nula es impar  PUNTO DE INFLEXION.


 f ´´ x i   0
 
 
 f ´´ x i   0 

 
   
Tambien podemos aplicar : x  x i  PUNTO DE INFLEXION   f ´´ xi   0 PUNTO DE INFLEXION   f ´´ x i   0 
   

 

 f ´´ x i  0

 f ´´ xi  0 
  

 
Ejemplo 1:
Determinar los puntos de inflexión y curvatura de la función: f  x   2 x  9 x  12 x .
3 2
 f ´ x 6 x2 18 x 12 3 9
 P1  ;  P. INFLEXION
2 2
f  x   2 x  9 x  12 x   f ´´ x 12 x 18
3 2
1.
 f ´´´ x 12

18 3
2. f ´´ x   0  12 x  18  0  x1  
12 2
3 
x  x 1   

 0 P 
f ´´
3
2
3 9
x1 ; f  x1    ;  PUNTO DE INFLEXION
 f ´´´   12  0
3.
2 3 1
2 2
 2 x1 =
3
2
CURVATURA
 3 3 3 
x    ;  x x   ; 
 2 2 2 
f ´´ x   0  3
CONVEXA    x    ; 
f ´´ x   12 x  18  f ´´ x   0 f ´´ x   0
 
 2
f ´´´ x   0
3 
CONCAVA    x   ; 
 
CONCAVA CONCAVA 2 
y  f  x   3 x  9 x  12 x 
3 2
HACIA ABAJO P. INFLEXION HACIA ARRIBA
 
   
 
OPTIMIZACION DE FUNCIONES
La optimización es una aplicación directa del cálculo diferencial y sirve para calcular máximos y mínimos de funciones sujetas a
determinadas condiciones. La aplicación práctica de los problemas de optimización es bien clara: calcular superficies o volúmenes
máximos, costes mínimos, forma óptima de determinadas figuras...
Es importante en este tipo de problemas identificar claramente la función a optimizar que suele depender de dos variables. El
ejercicio nos dará una condición que liga a ambas y lo que debemos hacer es despejar una de ellas y sustituirla en la función a
optimizar, de forma que tengamos una sola variable. A partir de aquí aplicaremos la teoría del cálculo diferencial para identificar
máximos o mínimos. Aquí van algunos ejemplos:
EJEMPLO 1.
Disponemos de 100 m. de alambre para vallar un campo rectangular. Calcula las dimensiones que debe tener dicho campo para que
la superficie vallada sea máxima.
2 x  2y  100
 S  x   x y Perimetro : 2x + 2y = 100 m.
   
 x  y  50  y  50  x  S x  x  50  x  S x  50 x  x 2 SUPERFICIE QUE QUEREMOS SEA MAXIMA
   
S  x   x  y
 

 S´ x   50  2 x
 S = x y
S  x   50 x  x 2   y
 S´´ x   2

S´ x   0  50  2 x  0  x  25 / S´´ 25  2  0  MAXIMO x
Las dimensiones del campo serán 25x25 m. Para que la superficie vallada sea máxima.
APLICACIONES DE DERIVADAS (Joaquín Aroca Gomez) Página 4 de 4