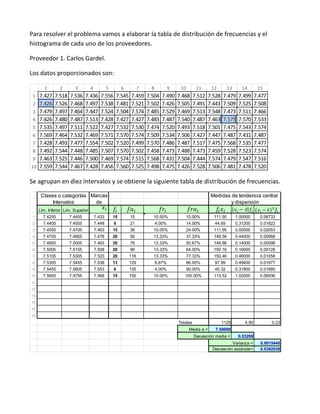
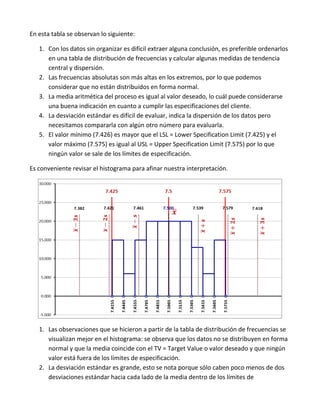
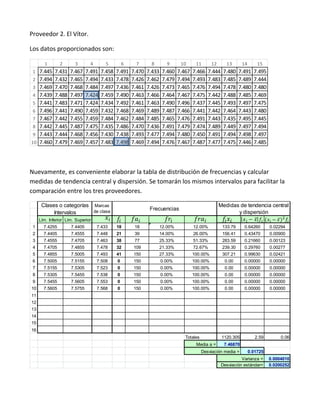
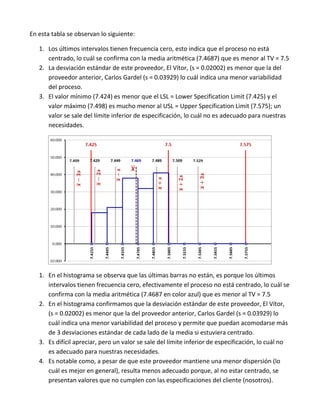
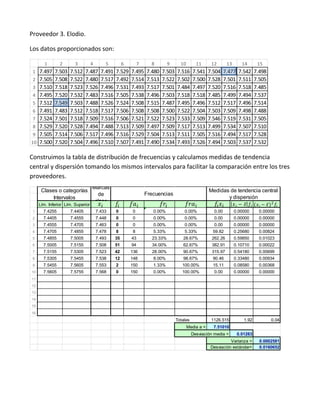
El documento presenta tres tablas de mediciones de diámetros de rodamientos de tres proveedores que se postulan para un contrato con una fábrica de microscopios. Se pide determinar cuál de los tres proveedores seleccionar basándose en un análisis de las tablas, histogramas y gráficas de cajas de los datos.

1. Mayo 2012
Histogramas
G. Edgar Mata Ortiz
Aplicaciones de histogramas y tablas de distribución de
frecuencias.
licmata@hotmail.com
http://licmata-math.blogspot.com
S http://www.slideshare.net/licmata/
C
Twitter: @licemata
http://www.facebook.com/licemata

2. Aplicaciones de los histogramas y tablas de distribución de frecuencias.
Lic. G. Edgar Mata Ortiz
Un histograma es una excelente herramienta para la descripción de conjuntos de datos
y, si se emplea adecuadamente, para la comparación de dichos conjuntos de datos.
En el siguiente ejercicio, elabora las tablas de distribución de frecuencias, los
histogramas y gráficos de cajas para cada conjunto de datos y contesta las preguntas
explicando detalladamente los argumentos para tus respuestas.
Importante: Utiliza las medias, medianas, modas y desviaciones estándar obtenidas en la tabla para
justificar tu elección, luego utiliza el histograma para confirmar o matizar tu decisión y finalmente
emplea la gráfica de cajas para argumentar tu posición. Elabora las conclusiones.
Ejercicio 1.
La fábrica de microscopios “Carolin” necesita elegir entre tres proveedores de
rodamientos de alta precisión. Se presentan 10 proveedores a la licitación, pero sólo
tres de ellos venden el material con las especificaciones indicadas (Las fábricas;
“Carlos Gardel”, “El Vítor” y “Elodio”) y al mismo costo. Se solicita a los tres
proveedores que envíen una muestra de 150 piezas con un diámetro de 7.5 ± 0.075
mm. Las medidas de los rodamientos de las tres empresas se encuentran en las
siguientes tablas. ¿Cuál empresa seleccionarías? ¿Por qué?
Tabla de mediciones correspondientes a la fábrica “Carlos Gardel S. A. de C. V.”
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 7.427 7.518 7.536 7.436 7.556 7.545 7.459 7.504 7.490 7.468 7.512 7.528 7.479 7.499 7.477
2 7.426 7.526 7.468 7.497 7.538 7.481 7.521 7.502 7.426 7.505 7.491 7.443 7.509 7.525 7.508
3 7.479 7.497 7.464 7.447 7.524 7.504 7.574 7.485 7.529 7.469 7.513 7.548 7.473 7.511 7.466
4 7.426 7.480 7.487 7.513 7.428 7.427 7.427 7.483 7.487 7.540 7.487 7.463 7.575 7.570 7.533
5 7.535 7.497 7.511 7.522 7.427 7.532 7.530 7.474 7.520 7.493 7.518 7.501 7.475 7.543 7.574
6 7.569 7.464 7.532 7.469 7.571 7.570 7.574 7.509 7.534 7.506 7.427 7.447 7.487 7.431 7.487
7 7.428 7.493 7.477 7.554 7.502 7.520 7.499 7.570 7.486 7.487 7.517 7.475 7.568 7.535 7.477
8 7.492 7.544 7.448 7.485 7.507 7.570 7.502 7.458 7.473 7.488 7.473 7.459 7.528 7.523 7.574
9 7.463 7.525 7.446 7.500 7.469 7.574 7.515 7.568 7.431 7.504 7.444 7.574 7.479 7.547 7.516
10 7.559 7.544 7.467 7.428 7.456 7.560 7.525 7.498 7.475 7.426 7.528 7.506 7.481 7.478 7.520

3. Tabla de mediciones correspondientes a la fábrica “El Vítor Incorporated”
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 7.445 7.431 7.467 7.491 7.458 7.491 7.470 7.433 7.460 7.467 7.466 7.444 7.480 7.491 7.495
2 7.494 7.432 7.465 7.494 7.433 7.478 7.426 7.462 7.479 7.494 7.493 7.483 7.485 7.489 7.444
3 7.469 7.470 7.468 7.484 7.497 7.436 7.461 7.426 7.473 7.465 7.476 7.494 7.478 7.480 7.480
4 7.439 7.488 7.497 7.424 7.459 7.490 7.463 7.466 7.464 7.467 7.475 7.442 7.488 7.485 7.469
5 7.441 7.483 7.471 7.424 7.434 7.492 7.461 7.463 7.490 7.496 7.437 7.445 7.493 7.497 7.475
6 7.496 7.441 7.490 7.459 7.432 7.468 7.469 7.489 7.487 7.466 7.441 7.442 7.464 7.443 7.480
7 7.467 7.442 7.455 7.459 7.484 7.462 7.484 7.485 7.465 7.476 7.491 7.443 7.435 7.495 7.445
8 7.442 7.445 7.487 7.475 7.435 7.486 7.470 7.436 7.491 7.479 7.474 7.489 7.449 7.497 7.494
9 7.443 7.444 7.468 7.456 7.430 7.438 7.493 7.477 7.494 7.480 7.450 7.491 7.494 7.498 7.497
10 7.460 7.479 7.469 7.457 7.483 7.498 7.469 7.494 7.476 7.467 7.487 7.477 7.475 7.446 7.485
Tabla de mediciones correspondientes a la fábrica “Elodio S. de R. L.”
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 7.497 7.503 7.512 7.487 7.491 7.529 7.495 7.480 7.503 7.516 7.541 7.504 7.477 7.542 7.498
2 7.505 7.508 7.522 7.480 7.517 7.492 7.514 7.513 7.522 7.502 7.500 7.528 7.501 7.511 7.505
3 7.510 7.518 7.523 7.526 7.496 7.531 7.493 7.517 7.501 7.484 7.497 7.520 7.516 7.518 7.485
4 7.495 7.520 7.532 7.483 7.516 7.505 7.538 7.496 7.503 7.518 7.518 7.485 7.499 7.494 7.537
5 7.512 7.549 7.503 7.488 7.526 7.524 7.508 7.515 7.487 7.495 7.496 7.512 7.517 7.496 7.514
6 7.491 7.483 7.512 7.518 7.517 7.506 7.508 7.508 7.500 7.522 7.504 7.503 7.509 7.498 7.488
7 7.524 7.501 7.518 7.509 7.516 7.506 7.521 7.522 7.523 7.533 7.509 7.546 7.519 7.531 7.505
8 7.529 7.520 7.528 7.494 7.488 7.513 7.509 7.497 7.509 7.517 7.513 7.499 7.534 7.507 7.510
9 7.505 7.514 7.506 7.517 7.496 7.516 7.529 7.504 7.513 7.511 7.505 7.516 7.494 7.517 7.528
10 7.500 7.520 7.504 7.496 7.510 7.507 7.491 7.490 7.534 7.493 7.526 7.494 7.503 7.537 7.532

4. Para resolver el problema vamos a elaborar la tabla de distribución de frecuencias y el
histograma de cada uno de los proveedores.
Proveedor 1. Carlos Gardel.
Los datos proporcionados son:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 7.427 7.518 7.536 7.436 7.556 7.545 7.459 7.504 7.490 7.468 7.512 7.528 7.479 7.499 7.477
2 7.426 7.526 7.468 7.497 7.538 7.481 7.521 7.502 7.426 7.505 7.491 7.443 7.509 7.525 7.508
3 7.479 7.497 7.464 7.447 7.524 7.504 7.574 7.485 7.529 7.469 7.513 7.548 7.473 7.511 7.466
4 7.426 7.480 7.487 7.513 7.428 7.427 7.427 7.483 7.487 7.540 7.487 7.463 7.575 7.570 7.533
5 7.535 7.497 7.511 7.522 7.427 7.532 7.530 7.474 7.520 7.493 7.518 7.501 7.475 7.543 7.574
6 7.569 7.464 7.532 7.469 7.571 7.570 7.574 7.509 7.534 7.506 7.427 7.447 7.487 7.431 7.487
7 7.428 7.493 7.477 7.554 7.502 7.520 7.499 7.570 7.486 7.487 7.517 7.475 7.568 7.535 7.477
8 7.492 7.544 7.448 7.485 7.507 7.570 7.502 7.458 7.473 7.488 7.473 7.459 7.528 7.523 7.574
9 7.463 7.525 7.446 7.500 7.469 7.574 7.515 7.568 7.431 7.504 7.444 7.574 7.479 7.547 7.516
10 7.559 7.544 7.467 7.428 7.456 7.560 7.525 7.498 7.475 7.426 7.528 7.506 7.481 7.478 7.520
Se agrupan en diez intervalos y se obtiene la siguiente tabla de distribución de frecuencias.
Clases o categorías Marcas Medidas de tendencia central
Intervalos de y dispersión
Lím. Inferior Lím. Superior
1 7.4255 7.4405 7.433 15 15 10.00% 10.00% 111.50 1.00500 0.06733
2 7.4405 7.4555 7.448 6 21 4.00% 14.00% 44.69 0.31200 0.01622
3 7.4555 7.4705 7.463 15 36 10.00% 24.00% 111.95 0.55500 0.02053
4 7.4705 7.4855 7.478 20 56 13.33% 37.33% 149.56 0.44000 0.00968
5 7.4855 7.5005 7.493 20 76 13.33% 50.67% 149.86 0.14000 0.00098
6 7.5005 7.5155 7.508 20 96 13.33% 64.00% 150.16 0.16000 0.00128
7 7.5155 7.5305 7.523 20 116 13.33% 77.33% 150.46 0.46000 0.01058
8 7.5305 7.5455 7.538 13 129 8.67% 86.00% 97.99 0.49400 0.01877
9 7.5455 7.5605 7.553 6 135 4.00% 90.00% 45.32 0.31800 0.01685
10 7.5605 7.5755 7.568 15 150 10.00% 100.00% 113.52 1.02000 0.06936
11 0 0.00% 100.00%
12 #N/A #N/A
13 #N/A #N/A #N/A #N/A
14 #N/A #N/A #N/A #N/A
15 #N/A #N/A #N/A #N/A
16 #N/A #N/A #N/A #N/A
Totales 1125 4.90 0.23
Media a = 7.50000
Desviación media = 0.03269
Varianza = 0.0015440
Desviación estándar= 0.0392938

5. En esta tabla se observan lo siguiente:
1. Con los datos sin organizar es difícil extraer alguna conclusión, es preferible ordenarlos
en una tabla de distribución de frecuencias y calcular algunas medidas de tendencia
central y dispersión.
2. Las frecuencias absolutas son más altas en los extremos, por lo que podemos
considerar que no están distribuidos en forma normal.
3. La media aritmética del proceso es igual al valor deseado, lo cuál puede considerarse
una buena indicación en cuanto a cumplir las especificaciones del cliente.
4. La desviación estándar es difícil de evaluar, indica la dispersión de los datos pero
necesitamos compararla con algún otro número para evaluarla.
5. El valor mínimo (7.426) es mayor que el LSL = Lower Specification Limit (7.425) y el
valor máximo (7.575) es igual al USL = Upper Specification Limit (7.575) por lo que
ningún valor se sale de los límites de especificación.
Es conveniente revisar el histograma para afinar nuestra interpretación.
1. Las observaciones que se hicieron a partir de la tabla de distribución de frecuencias se
visualizan mejor en el histograma: se observa que los datos no se distribuyen en forma
normal y que la media coincide con el TV = Target Value o valor deseado y que ningún
valor está fuera de los límites de especificación.
2. La desviación estándar es grande, esto se nota porque sólo caben poco menos de dos
desviaciones estándar hacia cada lado de la media dentro de los límites de

6. especificación, aunque ningún valor se encuentra fuera de estos límites, existen valores
demasiado cerca de estos extremos con el consiguiente riesgo de que, cualquier
variación del proceso pueda hacer que algunos valores queden fuera de especificación
y sean inadecuados para nuestro proceso.
3. La forma en que se distribuyen los datos, con valores altos en los extremos (primer y
último intervalo tiene frecuencias más grandes que el segundo y penúltimo), suele
indicar que algunos productos no cumplían con las especificaciones y fueron re-
trabajados para que cumplieran con los requerimientos.
En las siguientes páginas vamos a realizar el mismo análisis con los datos de los otros dos
proveedores.

7. Proveedor 2. El Vítor.
Los datos proporcionados son:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 7.445 7.431 7.467 7.491 7.458 7.491 7.470 7.433 7.460 7.467 7.466 7.444 7.480 7.491 7.495
2 7.494 7.432 7.465 7.494 7.433 7.478 7.426 7.462 7.479 7.494 7.493 7.483 7.485 7.489 7.444
3 7.469 7.470 7.468 7.484 7.497 7.436 7.461 7.426 7.473 7.465 7.476 7.494 7.478 7.480 7.480
4 7.439 7.488 7.497 7.424 7.459 7.490 7.463 7.466 7.464 7.467 7.475 7.442 7.488 7.485 7.469
5 7.441 7.483 7.471 7.424 7.434 7.492 7.461 7.463 7.490 7.496 7.437 7.445 7.493 7.497 7.475
6 7.496 7.441 7.490 7.459 7.432 7.468 7.469 7.489 7.487 7.466 7.441 7.442 7.464 7.443 7.480
7 7.467 7.442 7.455 7.459 7.484 7.462 7.484 7.485 7.465 7.476 7.491 7.443 7.435 7.495 7.445
8 7.442 7.445 7.487 7.475 7.435 7.486 7.470 7.436 7.491 7.479 7.474 7.489 7.449 7.497 7.494
9 7.443 7.444 7.468 7.456 7.430 7.438 7.493 7.477 7.494 7.480 7.450 7.491 7.494 7.498 7.497
10 7.460 7.479 7.469 7.457 7.483 7.498 7.469 7.494 7.476 7.467 7.487 7.477 7.475 7.446 7.485
Nuevamente, es conveniente elaborar la tabla de distribución de frecuencias y calcular
medidas de tendencia central y dispersión. Se tomarán los mismos intervalos para facilitar la
comparación entre los tres proveedores.
Clases o categorías Marcas Medidas de tendencia central
de clase
Frecuencias
Intervalos y dispersión
Lím. Inferior Lím. Superior
1 7.4255 7.4405 7.433 18 18 12.00% 12.00% 133.79 0.64260 0.02294
2 7.4405 7.4555 7.448 21 39 14.00% 26.00% 156.41 0.43470 0.00900
3 7.4555 7.4705 7.463 38 77 25.33% 51.33% 283.59 0.21660 0.00123
4 7.4705 7.4855 7.478 32 109 21.33% 72.67% 239.30 0.29760 0.00277
5 7.4855 7.5005 7.493 41 150 27.33% 100.00% 307.21 0.99630 0.02421
6 7.5005 7.5155 7.508 0 150 0.00% 100.00% 0.00 0.00000 0.00000
7 7.5155 7.5305 7.523 0 150 0.00% 100.00% 0.00 0.00000 0.00000
8 7.5305 7.5455 7.538 0 150 0.00% 100.00% 0.00 0.00000 0.00000
9 7.5455 7.5605 7.553 0 150 0.00% 100.00% 0.00 0.00000 0.00000
10 7.5605 7.5755 7.568 0 150 0.00% 100.00% 0.00 0.00000 0.00000
11 0 0.00% 100.00%
12 #N/A #N/A
13 #N/A #N/A #N/A #N/A
14 #N/A #N/A #N/A #N/A
15 #N/A #N/A #N/A #N/A
16 #N/A #N/A #N/A #N/A
Totales 1120.305 2.59 0.06
Media a = 7.46870
Desviación media = 0.01725
Varianza = 0.0004010
Desviación estándar= 0.0200252

8. En esta tabla se observan lo siguiente:
1. Los últimos intervalos tienen frecuencia cero, esto indica que el proceso no está
centrado, lo cuál se confirma con la media aritmética (7.4687) que es menor al TV = 7.5
2. La desviación estándar de este proveedor, El Vítor, (s = 0.02002) es menor que la del
proveedor anterior, Carlos Gardel (s = 0.03929) lo cuál indica una menor variabilidad
del proceso.
3. El valor mínimo (7.424) es menor que el LSL = Lower Specification Limit (7.425) y el
valor máximo (7.498) es mucho menor al USL = Upper Specification Limit (7.575); un
valor se sale del límite inferior de especificación, lo cuál no es adecuado para nuestras
necesidades.
1. En el histograma se observa que las últimas barras no están, es porque los últimos
intervalos tienen frecuencia cero, efectivamente el proceso no está centrado, lo cuál se
confirma con la media aritmética (7.4687 en color azul) que es menor al TV = 7.5
2. En el histograma confirmamos que la desviación estándar de este proveedor, El Vítor,
(s = 0.02002) es menor que la del proveedor anterior, Carlos Gardel (s = 0.03929) lo
cuál indica una menor variabilidad del proceso y permite que puedan acomodarse más
de 3 desviaciones estándar de cada lado de la media si estuviera centrado.
3. Es difícil apreciar, pero un valor se sale del límite inferior de especificación, lo cuál no
es adecuado para nuestras necesidades.
4. Es notable como, a pesar de que este proveedor mantiene una menor dispersión (lo
cuál es mejor en general), resulta menos adecuado porque, al no estar centrado, se
presentan valores que no cumplen con las especificaciones del cliente (nosotros).

9. Proveedor 3. Elodio.
Los datos proporcionados son:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 7.497 7.503 7.512 7.487 7.491 7.529 7.495 7.480 7.503 7.516 7.541 7.504 7.477 7.542 7.498
2 7.505 7.508 7.522 7.480 7.517 7.492 7.514 7.513 7.522 7.502 7.500 7.528 7.501 7.511 7.505
3 7.510 7.518 7.523 7.526 7.496 7.531 7.493 7.517 7.501 7.484 7.497 7.520 7.516 7.518 7.485
4 7.495 7.520 7.532 7.483 7.516 7.505 7.538 7.496 7.503 7.518 7.518 7.485 7.499 7.494 7.537
5 7.512 7.549 7.503 7.488 7.526 7.524 7.508 7.515 7.487 7.495 7.496 7.512 7.517 7.496 7.514
6 7.491 7.483 7.512 7.518 7.517 7.506 7.508 7.508 7.500 7.522 7.504 7.503 7.509 7.498 7.488
7 7.524 7.501 7.518 7.509 7.516 7.506 7.521 7.522 7.523 7.533 7.509 7.546 7.519 7.531 7.505
8 7.529 7.520 7.528 7.494 7.488 7.513 7.509 7.497 7.509 7.517 7.513 7.499 7.534 7.507 7.510
9 7.505 7.514 7.506 7.517 7.496 7.516 7.529 7.504 7.513 7.511 7.505 7.516 7.494 7.517 7.528
10 7.500 7.520 7.504 7.496 7.510 7.507 7.491 7.490 7.534 7.493 7.526 7.494 7.503 7.537 7.532
Construimos la tabla de distribución de frecuencias y calculamos medidas de tendencia
central y dispersión tomando los mismos intervalos para facilitar la comparación entre los tres
proveedores.
Marcas
Clases o categorías Medidas de tendencia central
de Frecuencias
Intervalos y dispersión
clase
Lím. Inferior Lím. Superior
1 7.4255 7.4405 7.433 0 0 0.00% 0.00% 0.00 0.00000 0.00000
2 7.4405 7.4555 7.448 0 0 0.00% 0.00% 0.00 0.00000 0.00000
3 7.4555 7.4705 7.463 0 0 0.00% 0.00% 0.00 0.00000 0.00000
4 7.4705 7.4855 7.478 8 8 5.33% 5.33% 59.82 0.25680 0.00824
5 7.4855 7.5005 7.493 35 43 23.33% 28.67% 262.26 0.59850 0.01023
6 7.5005 7.5155 7.508 51 94 34.00% 62.67% 382.91 0.10710 0.00022
7 7.5155 7.5305 7.523 42 136 28.00% 90.67% 315.97 0.54180 0.00699
8 7.5305 7.5455 7.538 12 148 8.00% 98.67% 90.46 0.33480 0.00934
9 7.5455 7.5605 7.553 2 150 1.33% 100.00% 15.11 0.08580 0.00368
10 7.5605 7.5755 7.568 0 150 0.00% 100.00% 0.00 0.00000 0.00000
11 0 0.00% 100.00%
12 #N/A #N/A
13 #N/A #N/A #N/A #N/A
14 #N/A #N/A #N/A #N/A
15 #N/A #N/A #N/A #N/A
16 #N/A #N/A #N/A #N/A
Totales 1126.515 1.92 0.04
Media a = 7.51010
Desviación media = 0.01283
Varianza = 0.0002581
Desviación estándar= 0.0160652

10. En esta tabla se observan lo siguiente:
1. Los primeros tres y el último intervalo tienen frecuencia cero, esto indica que el
proceso no está centrado, lo cuál se confirma con la media aritmética (7.5101) que es
mayor al TV = 7.5. Sin embargo, en este caso, ningún valor está fuera de los límites de
especificación.
2. La desviación estándar de este proveedor; Elodio (s = 0.01606), es menor que la del
proveedor uno; Carlos Gardel (s = 0.03929) y del proveedor dos; el Vítor (s = 0.02002),
lo cuál indica que tiene el mejor control de proceso de los tres proveedores.
3. El valor mínimo (7.477) es notablemente mayor que el LSL = Lower Specification Limit
(7.425) y el valor máximo (7.549) es menor al USL = Upper Specification Limit (7.575);
todos los valores están dentro de los límite de especificación, lo cuál indica que
cumplen, con holgura, con nuestros límites de especificación.
El histograma simplemente confirma nuestras primeras observaciones; es un proceso
aceptablemente centrado y que, sobre todo, presenta muy poca variabilidad, permitiendo
que puedan acomodarse 4 desviaciones estándar de cada lado de la media dentro de nuestros
límites de especificación.
Con esta información podemos recomendar que se elija al proveedor número 3. Elodio para
adquirir los rodamientos de alta precisión que necesitamos para nuestra fábrica.

11. Referencias bibliográficas.
Statistical Process Control
Leonard A. Doty.
Industrial Press Inc.
Business Statistics: For Contemporary Decision Making
Ken Black
Wiley & Sons
Control estadístico de los procesos.
José Francisco Vilar Barrio y Teresa Delgado Tejada
FC Editorial
Contenidos relacionados con la profesionalidad.
María Aránzazu García Cortázar
Ideaspropias Editorial.