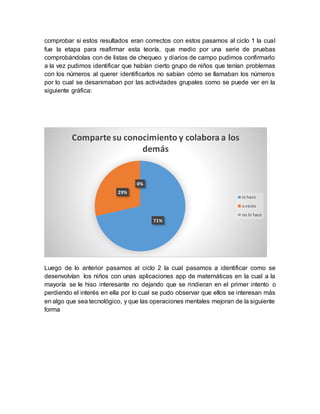
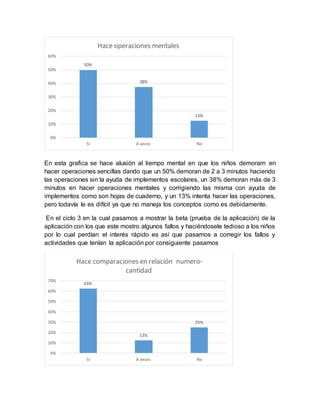
El documento describe una investigación sobre el uso de una aplicación Android para mejorar el aprendizaje de la resolución de problemas matemáticos en niños. La investigación encontró que los niños se interesaron más y mejoraron sus habilidades cuando usaron la aplicación de manera lúdica. Tras corregir fallas iniciales, la aplicación mostró ser una herramienta efectiva para hacer que el aprendizaje de las matemáticas sea más entretenido y significativo.

1. APLICACIÓN ANDROID COMO HERRAMIENTA DE APRENDIZAJE DE LA
RESOLUCION DE PROBLEMAS
AUTORES:
BOLAÑOS VALDES KEVIN JOSE
ARENAS DIAZ REINALDO
CARO RODRIGUEZ ANGIE YORLEY
ESCUELA NORMAL SUPERIOR DE ACACIAS
PROGRAMA DE FORMACIÓN COMPLEMENTARIA
CUARTO SEMESTRE
ACACIAS
2017

3. APLICACIÓN ANDROID COMO HERRAMIENTA DE
APRENDIZAJE DE RESOLUCION DE PROBLEMAS
Arenas Reinaldo
Bolaños Kevin
Angie Caro
Escuela Normal Superior de Acacias
kevin-zid@hotmail.com
Resumen
“la matemática ha construido, tradicionalmente, la tortura de los escolares del
mundo entero, y la humanidad ha tolerado esta tortura para sus hijos como un
sufrimiento inevitable para adquirir un conocimiento necesario; pero la enseñanza
no debe ser una tortura, y no seriamos buenos profesores al no procurar, por todos
los medios, transformar este sufrimiento en goce, lo cual no significa usencia de
esfuerzo, sino por el contrario, alumbramiento de estímulos y de esfuerzos
deseados y eficaces”. mediante la resolución de problemas, los estudiantes pueden
experimentar la potencia y utilidad de la matemática en el mundo que los rodean, y
para esto se utilizará una aplicación Android, dado a la incursión tecnológica, a los
niños les parecerá más interesante dejando potenciar esta dimensión.
Palabras clave
Resolución de problemas, matemáticas, tics, estrategias, aplicación
Abstrac
"Mathematics has traditionally built the torture of schoolchildren from all over the
world, and humanity has tolerated this torture for their children as an inevitable
suffering to acquire necessary knowledge; but the teaching should not be torture,
and we would not be good teachers by not trying, by all means, to transform this
suffering into enjoyment, which does not mean the absence of effort, but on the
contrary, enlightenment of stimuli and of desired efforts and effective. " by solving
problems, students can experience the power and usefulness of mathematics in the
world around them, and for this an Android application will be used, given the

4. technological incursion, children will find it more interesting to let this dimension be
enhanced .
Keywords
Problem solving, math, tics, strategies, application
Introducción
“la matemática ha construido, tradicionalmente, la tortura de los escolares del
mundo entero, y la humanidad ha tolerado esta tortura para sus hijos como un
sufrimiento inevitable para adquirir un conocimiento necesario; pero la enseñanza
no debe ser una tortura, y no seriamos buenos profesores al no procurar, por todos
los medios, transformar este sufrimiento en goce, lo cual no significa usencia de
esfuerzo, sino por el contrario, alumbramiento de estímulos y de esfuerzos
deseados y eficaces”. (Puig Adam)
La compresión que forman los autores sobre el termino resolución de problemas
toman como “el desarrollo de habilidades relacionadas con la gestión de procesos
y los contenidos matemáticos implicados en las resoluciones especialmente en los
procedimientos”
Como basan su modelo de enseñanza en dos ideas fundamentales en cuanto al
actuar del docente y los estudiantes frente a las tareas que se proponen, en este
artículo científico nos habla de que el docente debe motivar y hacer actuar al
estudiante, lo cual me parece muy importante, ya que exponemos a nuestros
estudiantes a nuevas formas de enseñanza en las que se modifican los roles
tradicionales de profesor y estudiante, del conocimiento que se pretende, se basan
en un modelo de enseñanza relacionada con la forma del docente y los estudiantes,
se busca que los estudiantes sean los protagonistas de su aprendizaje, estudiantes
que construyan su propio conocimiento, generando en ellos curiosidad e interés
para su resolución.
Es por esto que se ha optado por buscar nuevas metodologías para hacer que las
matemáticas sean más “divertidas” por asi decirlo. Aplicando las nuevas tecnologías
y el interés que muestra la generación de ahora desde temprana edad se pudo
evidencias buenos resultados.
Hablamos que desde los años 80, algunos investigadores, como Schoenfeld (1987),
adaptan la definición de Flavell sobre meta cognición a la resolución de problemas,
son pocos los profesores que han llevado a la práctica y han dado la importancia
que se merecen a aspectos tales como las creencias, las intuiciones, las emociones
o cómo controlan los propios estudiantes lo que hacen cuando resuelven problemas.

5. Ellos fijan su atención en esta última cuestión, relacionada con la gestión en los
procesos de resolución y su enseñanza y aprendizaje en las aulas de matemáticas,
buscan que los estudiantes logren relacionar las actividades de resolución de
problemas que realizan en el aula con la realidad.
Es por eso que al iniciar la investigación seleccionamos como sujeto de muestra a
los niños del grado transición del instituto educativo santa teresita con en el fin de
poder estudiar su interés desde el principio de la primaria. Una vez se escogió al
sujeto de objeto de observación se paso ha hacer una investigación de 4 pasos que
fueron
Descripción del trabajo
Ciclo 0 en esta esta etapa decidimos hacer una serie de actividades donde ellos
escogerían el número y la cantidad correcta del número que correspondiese en la
cual la gran mayoría fallo, de esta manera pasamos analizar cada uno de los
resultados que ellos sacaron mediante listas de chequeo y diarios de campo los
cuales se pueden ver resultados en la siguiente grafica
El 64% de los niños de institución educativa conoce los números de una y dos cifras
de tres cifras solo conocen hasta el 110, un 22% se confunden con pocos números
y el 14 % tienen dificultades para reconocer algunos números, con lo que resulto
poco interés de los niños por la materia así que esto nos dio paso libre para ejecutar
la investigación, pero teníamos que estar seguro de esto así que pasamos a
64%
22%
14%
Identifica las formasy nombres de los
números
IDENTIFICA
A VECES
NO IDENTIFICA

6. comprobar si estos resultados eran correctos con estos pasamos al ciclo 1 la cual
fue la etapa para reafirmar esta teoría, que medio por una serie de pruebas
comprobándolas con de listas de chequeo y diarios de campo pudimos confirmarlo
a la vez pudimos identificar que habían cierto grupo de niños que tenían problemas
con los números al querer identificarlos no sabían cómo se llamaban los números
por lo cual se desanimaban por las actividades grupales como se puede ver en la
siguiente gráfica:
Luego de lo anterior pasamos al ciclo 2 la cual pasamos a identificar como se
desenvolvían los niños con unas aplicaciones app de matemáticas en la cual a la
mayoría se le hiso interesante no dejando que se rindieran en el primer intento o
perdiendo el interés en ella por lo cual se pudo observar que ellos se interesan más
en algo que sea tecnológico, y que las operaciones mentales mejoran de la siguiente
forma
71%
29%
0%
Comparte su conocimiento y colabora a los
demás
lo hace
a veces
no lo hace

7. En esta grafica se hace alusión al tiempo mental en que los niños demorarn en
hacer operaciones sencillas dando que un 50% demoran de 2 a 3 minutos haciendo
las operaciones sin la ayuda de implementos escolares, un 38% demoran más de 3
minutos en hacer operaciones mentales y corrigiendo las misma con ayuda de
implementos como son hojas de cuaderno, y un 13% intenta hacer las operaciones,
pero todavía le es difícil ya que no maneja los conceptos como es debidamente.
En el ciclo 3 en la cual pasamos a mostrar la beta (prueba de la aplicación) de la
aplicación con los que este mostro algunos fallos y haciéndosele tedioso a los niños
por lo cual perdían el interés rápido es así que pasamos a corregir los fallos y
actividades que tenían la aplicación por consiguiente pasamos
50%
38%
13%
0%
10%
20%
30%
40%
50%
60%
Si A veces No
Hace operaciones mentales
63%
13%
25%
0%
10%
20%
30%
40%
50%
60%
70%
Si A veces No
Hace comparaciones en relación numero-
cantidad

8. En el ciclo 4 la cual mostrábamos la aplicación ya corregida, dando como resultado
gran interés a los niños por esta, la cual este fue el resultado
En las preguntas que se hicieron se analizaron aspectos claros como si el estudiante se
demora menos de 2, 5 y más 5 minutos realizando correctamente las operaciones con la
finalidad de analizar si conoce la simbología de números, operaciones a su vez si conoce
la correcta secuencia y la cantidad de cada número. Se reunieron todas estas variables en
esta lista de chequeo y de la se pudo observar que un 75% del alumno relacionan
debidamente las matemáticas con su contexto relacionando las cantidades y conteo de las
cosas quedando demostrado en la app, un 13 % a veces se confunden en sus resultados
pero en logra hacer las cosas y un 13 % no relaciona con su contexto las matemáticas
errando cada número que dice
Conclusiones
se evidenció que como herramienta una app de resolución de problemas matemáticos la
apropiación de competencias en las matemáticas mediante la aplicación de planes de
acción con la ayuda de instrumentos como lista de chequeo, encuesta y registros
anecdóticos, también cómo a través de la realización de diferentes estrategias innovadoras
hubo mejoría por parte de los estudiantes en cuanto a la resolución de problemas
se pudo concluir que no son lo suficientemente atractivas las clases para ellos por lo tanto
no hay un verdadero aprendizaje ni apropiación de competencias dado a que no están tan
75%
13% 13%
0%
10%
20%
30%
40%
50%
60%
70%
80%
S I A V EC ES N O
LISTA DE CHEQUEO
todas la preguntas

9. interesados por la clase, no hay tanta participación, curiosidad, interés, gusto etc. como el
profesor quiere
Bibliografía
1. A. Fernández Bravo -DESARROLLO DEL PENSAMIENTO MATEMÁTICO EN
EDUCACIÓN INFANTIL J.
2. MYRIAM ESTHER ORTIZ PADILLA* Universidad Simón Bolívar - Colombia Instituto
Nacional de Formación Técnica Profesional Humberto Velásquez García –Colombia -
COMPETENCIA MATEMÁTICA EN NIÑOS EN EDAD PREESCOLAR
3. EDGAR OLIVER CARDOSO ESPINOSA MARÍA TRINIDAD CERECEDO
MERCADO El desarrollo de las competencias matemáticas en la primera infancia
4. Ministerio Educación de Nacional-ESTÁNDARES BÁSICOS DE COMPETENCIAS
EN MÁTEMÁTICAS 2003
5. Yadira Méndez Acosta-Estrategias para la enseñanza del preescolar+
6. María Frontera Sancho-ADQUISICION DE LOS CONCEPTO MATEMATICOS
BASICOS. UNA PERSPECTIVA COGNITIVA TOMO 1