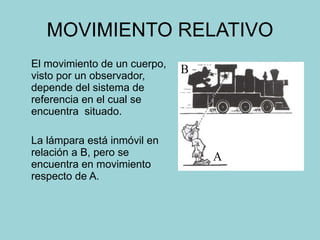
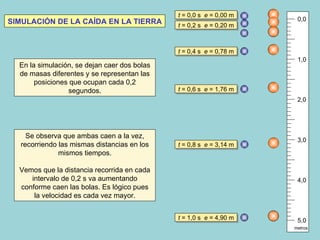
Este documento presenta los conceptos fundamentales de la caída libre y el movimiento vertical. Explica que en la caída libre, sin rozamiento con el aire, todos los cuerpos caen a la misma velocidad independientemente de su masa. También analiza el lanzamiento vertical hacia arriba como un caso particular de movimiento retardado uniformemente. Finalmente, incluye ejemplos numéricos y gráficos para ilustrar estos conceptos.

1. Estudio del movimiento de Caída Libre de los cuerpos. Un caso especial del M.R.U.V. Adaptado por Juan Vásquez – fuente slide share

2. OBJETIVOS Al término de la clase deberás: Caracterizar y analizar movimientos verticales. Aplicar las ecuaciones de movimientos verticales a la solución de problemas. Interpretar información en gráficos.

3. CAÍDA DE LOS CUERPOS En la caída de los cuerpos en la Tierra distinguimos dos situaciones diferentes según se tenga o no en cuenta el rozamiento con el aire. ROZAMIENTO IMPORTANTE ROZAMIENTO DESPRECIABLE

4. CAÍDA LIBRE Llamamos caída libre a la de los cuerpos cuando se pueda considerar despreciable el rozamiento con el aire. Una situación ideal para experimentar la caída libre es la caída de los cuerpos en la Luna. La Luna no tiene atmósfera, por lo que cuando un cuerpo caiga en la Luna no rozará con nada.

5. CAÍDA LIBRE Llamamos caída libre a la de los cuerpos cuando se pueda considerar despreciable el rozamiento con el aire. Una situación ideal para experimentar la caída libre es la caída de los cuerpos en la Luna. La Luna no tiene atmósfera, por lo que cuando un cuerpo caiga en la Luna no rozará con nada.

6. Scott : Bien, en mi mano izquierda tengo una pluma y en la derecha un martillo. Y supongo que una de las razones por la que estamos hoy aquí es por un caballero llamado Galileo, porque hace mucho tiempo hizo un importante descubrimiento sobre los cuerpos que caen en un campo gravitatorio. Y pensamos que la Luna sería el mejor lugar para confirmar sus ideas. [Fendell enfoca con el zoom el martillo y la pluma y después retrocede con la cámara para que se aprecie la escena] Scott: Ahora lo intentaremos para que lo veas. Concretamente, la pluma es de un halcón, de nuestro Halcón (se refiere al halcón del escudo USA). Ahora soltaremos los dos a la vez y, esperemos, llegarán a la vez al suelo. (Pausa) Suelta simultáneamente el martillo y la pluma. El martillo y la pluma chocan contra el suelo prácticamente a la vez. Scott : ¡qué te parece!; Allen: ¡qué te parece! (Aplausos en Houston) Scott : Lo que demuestra que las ideas de Galileo eran correctas. (Pausa) Trascripción de los comentarios que se oyen en el video.

7. Si dos cuerpos de diferente masa, caen libremente en las proximidades de la superficie de la Tierra lo hacen de igual manera. Independiente de la masa, ambos caen con movimiento uniformemente acelerado. Cada segundo, la velocidad del cuerpo aumenta en 9,8 m/s. Eso supone que la aceleración es de 9,8 m/s 2 . Si caen desde la misma altura, con la misma velocidad inicial, llegarán al suelo simultáneamente, aunque las masas sean diferentes. Si se trata de un cuerpo que es lanzado hacia arriba, una vez que está subiendo libremente, su velocidad disminuye cada segundo en 9,8 m/s. Lejos de la superficie de la Tierra, la aceleración de caída o subida es menor. Pero para que la disminución sea importante hay que alejarse bastante. Por ejemplo, dentro de un avión en vuelo, la caída de los cuerpos ocurre con aceleración casi igual que en la superficie de la Tierra. LA CAÍDA EN LAS PROXIMIDADES DE LA TIERRA

8. En la simulación, se dejan caer dos bolas de masas diferentes y se representan las posiciones que ocupan cada 0,2 segundos. SIMULACIÓN DE LA CAÍDA EN LA TIERRA t = 0,0 s e = 0,00 m t = 0,2 s e = 0,20 m t = 0,4 s e = 0,78 m t = 0,6 s e = 1,76 m t = 0,8 s e = 3,14 m t = 1,0 s e = 4,90 m Se observa que ambas caen a la vez, recorriendo las mismas distancias en los mismos tiempos. Vemos que la distancia recorrida en cada intervalo de 0,2 s va aumentando conforme caen las bolas. Es lógico pues la velocidad es cada vez mayor. 0,0 1,0 2,0 3,0 4,0 5,0 metros

9. Caída Libre En ausencia de la resistencia del aire, todos los cuerpos, independientemente de su peso, masa, forma o composición, al dejárseles libre, caen hacia la superficie terrestre debido a la atracción que ejerce la Tierra.

10. Análisis gráfico de caída libre

11. Sugerencias para resolver problemas de cinemática Identificar las condiciones iniciales y finales. Traducir a símbolos las expresiones verbales como por ejemplo: “se lanza hacia abajo una pelota con una rapidez de 20 m/s”. Traducido a simbología matemática equivale a v 0 = - 20 m/s. En el MODELO FÍSICO detectar puntos de interés y en forma horizontal, escribir todas las variables , asignándole los valores correspondientes, en caso de que desconozca alguna de ellas, la igualará con un signo de interrogación. En la resolución del problema, se debe cuestionar a uno mismo: ¿Qué me piden? “la variable desconocida ” ¿Cuándo que? “ los datos de las variables que se relacionan con esa variable desconocida”, ya sean condiciones finales y/o iniciales. De las ecuaciones de movimiento (MODELOS MATEMATICOS) seleccionar aquellas que involucren la variable desconocida y por eliminación descartar aquellas que contengan variables que desconozca y que el problema no proporciona, las cuales generalmente se solicitan en una pregunta posterior. Con lo anterior, el problema queda completamente bosquejado. Realizar operaciones algebraicas (despejar la variable), sustitución y operaciones aritméticas.

13. MOVIMIENTOS VERTICALES Y RELATIVOS

14. CAÍDA LIBRE Es un caso particular de movimiento rectilíneo uniformemente acelerado. La velocidad inicial es 0 m/s. La aceleración es g.

15. TRANSFORMACIÓN DE LAS ECUACIONES DE MOVIMIENTO CAÍDA LIBRE Por efectos prácticos, ubicaremos el origen del sistema en la posición inicial del cuerpo y apuntando hacia abajo. y 0

16. GUÍA Nº 01 EJERCICIO Nº 1 ¿Con qué rapidez llega al suelo un objeto que se deja caer libremente y demora 40[s] en impactar en él? A) 400 [m/s] B) 200 [m/s] C) 100 [m/s] D) 20 [m/s] E) 5 [m/s]

17. REPRESENTACIÓN GRÁFICA CAÍDA LIBRE Los gráficos itinerario, velocidad y aceleración, según origen del sistema de referencia en el suelo o en el punto donde se suelta el móvil.

18. LANZAMIENTO VERTICAL HACIA ARRIBA Es un caso particular de movimiento rectilíneo uniformemente retardado. La aceleración que actúa sobre el móvil es -g , cuando el eje apunta a favor del movimiento.

19. TRANSFORMACIÓN DE LAS ECUACIONES DE MOVIMIENTO LANZAMIENTO VERTICAL HACIA ARRIBA Considerando el eje coordenado a favor del movimiento.

20. EJERCICIO 2 Desde el suelo se lanza verticalmente hacia arriba un objeto a 40 [m/s]. Despreciando la resistencia del aire, determine a qué altura está a los 3[s]. A) 210[m] B) 165[m] C) 75[m] D) 50[m] E) 30[m]

21. CONSIDERACIONES ESPECIALES El tiempo que demora el móvil en subir es el mismo que demora en bajar. La rapidez para cada punto de subida es la misma que de bajada (la velocidad difiere en el signo).

22. EJERCICIO 3 Desde el suelo se lanza verticalmente hacia arriba un objeto a 40 [m/s]. Despreciando la resistencia del aire, determine cuánto tiempo estuvo en el aire. A) 10[s] B) 8[s] C) 6[s] D) 4[s] E) 2[s]

23. REPRESENTACIÓN GRÁFICA LANZAMIENTO VERTICAL HACIA ARRIBA Los gráficos itinerario, velocidad y aceleración, según origen del sistema de referencia.

24. TRANSFORMACIÓN DE LAS ECUACIONES DE MOVIMIENTO LANZAMIENTO VERTICAL HACIA ABAJO Por efectos prácticos, ubicaremos el origen del sistema en la posición inicial del cuerpo y apuntando hacia abajo.

25. EJERCICIO 4 Se lanza verticalmente hacia abajo un objeto con rapidez inicial de 2[m/s], llegando al suelo a 12[m/s]. Determine desde qué altura fue lanzado. A) 14[m] B) 12[m] C) 10[m] D) 7[m] E) 5[m]

26. MOVIMIENTO RELATIVO El movimiento de un cuerpo, visto por un observador, depende del sistema de referencia en el cual se encuentra situado. La lámpara está inmóvil en relación a B, pero se encuentra en movimiento respecto de A.

27. EJERCICIO 5 Dos móviles vienen al encuentro uno del otro con la misma rapidez v. El módulo de la velocidad que percibe cualquiera de los móviles respecto del otro es: I. 2v II. –2v III. 0 A) Sólo I B) Sólo II C) Sólo III D) Sólo I o II E) Ninguna

28. EJERCICIO 6 En cierto instante un barco se mueve con velocidad v2 respecto del mar, tal como indica la figura. Sobre éste, una persona corre con una velocidad v3. Si el mar se mueve con una velocidad constante v1 y considerando el sistema de referencia positivo hacia la derecha en todos los casos, ¿con qué velocidad ve desplazarse la persona A, situada en una isla, a la persona B? A) v1 + v2 + v3 B) v1 + v2 – v3 C) v2 – v3 D) v2 + v3 E) v1 + v3

29. SÍNTESIS DE LA CLASE Movimientos Uniforme Rectilíneo Uniforme Acelerados Verticales Horizontales M.R.U.A. M.R.U.R. Relativos Hacia abajo Hacia arriba Caída libre

30. ¿QUÉ APRENDÍ? Caracterización y análisis de movimientos verticales. Aplicación de las ecuaciones de movimientos verticales a la solución de problemas. Interpretación de información en gráficos.

31. DESCRIPCIÓN DE LAS ACTIVIDADES/DIDÁCTICAS Observan un video de caída libre. Ingresan al SLIDESHARE del Internet. Haz un clic en el enlace siguiente para visualizar el APPLET de caída libre: http://www.xtec.cat/~ocasella/applets/caiguda/appletsol2.htm Haz un clic en el enlace siguiente para visualizar los ejercicios propuestos de caída libre: http://issuu.com/ernestoyanezrivera/docs/namefb9a44