Aplicaciones de la derivada: recta tangente, normal, máximos y mínimos

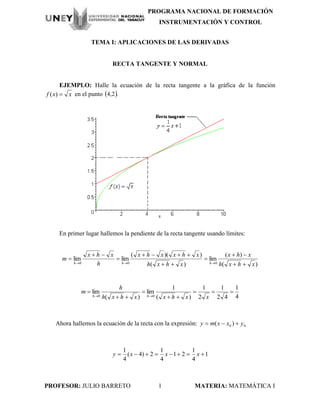
PROGRAMA NACIONAL DE FORMACIÓN
INSTRUMENTACIÓN Y CONTROL
PROFESOR: JULIO BARRETO 1 MATERIA: MATEMÁTICA I
TEMA I: APLICACIONES DE LAS DERIVADAS
RECTA TANGENTE Y NORMAL
EJEMPLO: Halle la ecuación de la recta tangente a la gráfica de la función
xxf )( en el punto  .2,4
En primer lugar hallemos la pendiente de la recta tangente usando límites:
)(
)(
lim
)(
))((
limlim
000
xhxh
xhx
xhxh
xhxxhx
h
xhx
m
hhh









4
1
42
1
2
1
)(
1
lim
)(
lim
00





 xxhxxhxh
h
m
hh
Ahora hallemos la ecuación de la recta con la expresión: 00 )( yxxmy 
1
4
1
21
4
1
2)4(
4
1
 xxxy

TEMA I: APLICACIONES DE LA DERIVADA
La normal a una curva en un punto P es la perpendicular a la recta tangente en
dicho punto. Si la pendiente de la tangente es ),(' afmt  la pendiente de la normal será
)('
1
af
mN  y la ecuación de la normal nos viene dada por:
)(
)('
1
)( ax
af
afy 
Así, en el ejercicio anterior la pendiente de la normal será .4
4
1
1
Nm Y la
ecuación de la normal nos viene dada por:
104284)2(42  xyxyxy
Grafique esta recta como ejercicio.
EJERCICIO:
Hallar la ecuación de la recta tangente y normal a la curva dada por 3
)( xxf  en
el punto de abscisa x = 2.
Ecuación de la recta tangente: 162  xy
Ecuación de la recta normal:
6
49
12

x
y
INFORMACIÓN EXTRAIDA DE LA PRIMERA DERIVADA
PUNTO CRÍTICO
DEFINICIÓN: Un número c para el cual una función f está definida y para el cual
  0 cf o  cf  no existe, se llama un NÚMERO CRÍTICO para f .
EJEMPLO: La función f está definida por la ecuación   .
2
2x-
xexf  ¿Cuáles son
los puntos críticos de f ?

Para empezar, debemos determinar el dominio de   .
2
2x-
xexf 
.RDomf 
Tenemos que encontrar la derivada de  
2
2x-
xexf  para determinar los puntos
críticos. Por la regla del producto y la regla de la cadena,
        222222
2222222
441 x-x-x-x-x-x-
exexexeexexxf 




Igualamos esta expresión a 0 y resolvemos la ecuación resultante.
  04104 22222 222
 xeexe x-x-x-
Como 0
2
2
x-
e para toda x , se sigue que
    
2
1
02121041 2
 x=x+xx
Así,
2
1
x son los ceros de f ′. Esto significa que los puntos críticos
son
2
1
y
2
1
 . Ahora bien, observa la gráfica siguiente y ten en cuenta la relación entre
derivada en un punto y la pendiente de la recta tangente a la curva en ese punto.

RELACIÓN ENTRE CRECIMIENTO Y DERIVADA
 f derivable y creciente en 0x  0)( 0  xf .
 f derivable y decreciente en 0x  0)( 0  xf .
EJEMPLO:   3
xxf  es derivable en todo R y su derivada es   2
3xxf  . La
gráfica es:
Se observa que la función es creciente en todo su dominio que es R , veamos que la
derivada es positiva en todo punto del dominio.
Efectivamente 03)( 2
 xxf Rxtodopara .
CRITERIO PARA IDENTIFICAR INTERVALOS CRECIENTES O
DECRECIENTES
 fxf  0)( es creciente.
 fxf  0)( es decreciente.
MÁXIMOS Y MÍNIMOS RELATIVOS
 La función f presenta un máximo relativo en ,0x cuando existe un entorno  0xE
tal que:    0xfxf    ., 00 xxxEx 

 La función f presenta un mínimo relativo en ,0x cuando existe un entorno  0xE
tal que:    0xfxf    ., 00 xxxEx 
CONDICIÓN NECESARIA DE MÁXIMO O MÍNIMO RELATIVO
f es derivable en 0x y f tiene un máximo o un mínimo en
0x 0)( 0  xf .
Sin embargo no es una condición suficiente, porque puede ocurrir que la derivada en
un punto valga 0 y que no haya máximo ni mínimo, como en 00 x en el ejemplo 3
xy  .
REGLA PARA SABER SI UN PUNTO SINGULAR ES MÁXIMO O MÍNIMO
RELATIVO
Para saber si un punto singular (puntos que anulan la derivada) es máximo o mínimo
relativo de una función estudiaremos el signo de la derivada primera de la función.
EJEMPLO: Sea   xxxf 273
 cuya grafica es:
SOLUCIÓN:

Si calculamos su derivada y estudiamos el signo se tiene,
       .33393273 22
 xxxxxf Luego podríamos decir que la función de
acuerdo con este estudio:
 Crece en     ,33,
 Decrece en  3,3
Así como crece en  3, y decrece en  3,3 entonces hay un máximo relativo en
 )3(,3  f que en este caso será un MÁXIMO ABSOLUTO y como decrece en  3,3 y
crece en  ,3 entonces hay un mínimo relativo en  )3(,3 f que en este caso será un
MÍNIMO ABSOLUTO cómo se observaba en la gráfica.
INFORMACIÓN EXTRAIDA DE LA SEGUNDA DERIVADA
Una función es cóncava en un intervalo si las rectas tangentes a la función en ese
intervalo están por debajo de la función. Una función es convexa en un intervalo si las
rectas tangentes a la función de ese intervalo están por encima.
La denominación de convexidad y concavidad depende del punto de vista que se
adopte para considerar que es una concavidad, esto es si se mira a la función "desde arriba"
o "desde abajo". Por ello, es frecuente que en ocasiones se adopten las denominaciones
cóncava hacia arriba y cóncava hacia abajo para evitar las ambigüedades.
Los puntos donde la función cambia de curvatura se llaman PUNTOS DE
INFLEXIÓN.
(  , -3) (-3,3) (3,)
3 + + +
 3x - + +
 3x - - +
Signo f  + - +

RELACIÓN DE LA CURVATURA CON LA SEGUNDA DERIVADA
Si observamos la gráfica siguiente veremos que cuando la función es cóncava las
pendientes de las rectas tangentes (las derivadas) tienen un valor cada vez más grande, y
cuando es convexa cada vez menor.
CRITERIOS DE CONCAVIDAD O CONVEXIDAD
 Por la derivada primera:
a. Si una función es cóncava las pendientes de las tangentes aumentan ( f es
creciente).
b. Si una función es convexa las pendientes de las tangentes disminuyen ( f  es
decreciente).
 Por la derivada segunda:
Si f es cóncava hacia arriba  entonces f  creciente, por lo tanto .0f
Si f es cóncava hacia abajo  entonces f  decreciente, por lo tanto .0f
f es derivable en 0x y tiene un PUNTO DE INFLEXIÓN en 0x    00  xf

CRITERIO PARA IDENTIFICAR INTERVALOS CÓNCAVOS Y CONVEXOS
Si una función es derivable dos veces, se tiene
 fxf  0)( es cóncava.
 fxf  0)( es convexa.
EJEMPLO: Utilice el criterio de la segunda derivada para encontrar los extremos de
la función indicada:
  xx= xxf 156 23

SOLUCIÓN: Tenemos que que su dominio es: .Domf=R Además:
   015123 2
xx=xf PUNTOS CRÍTICOS: 5y1 21 .=x=x 
   0126x=xf    0181=f En 11 = -x se tiene un MÁXIMO de f .
   0185 =f En 52 =x se tiene in MÍNIMO de f .
EJEMPLO: Sea la función   .x
=xexf Hallar el punto de inflexión y donde la
función es cóncava y convexa.
SOLUCIÓN: Notemos que su dominio es: .Domf=R
Ahora bien hallando la primera derivada:
        .11 xxxxxxx
exxeeexeexex=xf 


 
Y la segunda derivada es:

            xxxxxxxxxxx
exxeexeeeexexexee=xf 







 22
El punto de inflexión es:
    020  x
ex=xf
Y como 0x
e para todo ,x entonces .202  xx Y el PUNTO DE
INFLEXIÓN es .
2
,2 2 




 

e
El signo de f  es     0323 33
 
eef y     .0121 11
 
eef
Así la función es convexa en  2, y cóncava en  .,2  Veamos:
APLICACIONES A RAZONES DE CAMBIO
Según lo dicho anteriormente, el concepto de razón de cambio está presente en la vida
diaria, muchas veces manejado sin darle un nombre específico o sin reflexionar sobre las
acciones realizadas. Ya que vivimos en un mundo físico, social, político, económico,
biológico, resulta importante poder describir y medir estos cambios a través de modelos
matemáticos. Por ejemplo, una planta crece a medida que el tiempo transcurre, puede
detener su crecimiento en algún instante, para luego volver a crecer, o permanecer
estacionaria. También la población de un país varía con el correr del tiempo y la variación
depende básicamente de la cantidad de nacimientos y de muertes.
Es importante medir estas variaciones y expresarlas en números pues estos nos
permitirán extraer conclusiones. Esto nos permite saber, por ejemplo, en el caso de
consumo de energía eléctrica como función del tiempo, cuándo se produce un aumento

repentino, lo que indica la necesidad de aumentar la capacidad eléctrica; si estamos
analizando la evolución de una enfermedad a través del tiempo podremos saber cuándo se
está propagando con mayor rapidez y así reforzar las medidas sanitarias necesarias.
Analizaremos a través de ejemplos, cómo medir los cambios.
EJEMPLO 1: Un pedazo de alambre de 20 cm de largo se corta en dos partes; una
parte se dobla para formar un cuadrado y con la otra se forma una circunferencia. ¿Dónde
se deberá hacer el corte para que la suma de las áreas del cuadrado y del círculo sea un
mínimo?
SOLUCIÓN:
Con el primer segmento se construye el cuadrado cuyo lado medirá que su dominio
es: ,
4
x
con el resto se construye la circunferencia en que el radio medirá que su dominio es:
.
2
2



xL
rxLr Las áreas, por lo tanto, medirán:
2
cuadrado
16
1
=A x
y
 
4
=A
2
círculo
xL
El área total será:
 
416
1
=AA=A
2
2
círculocuadradoTotal
xL
x


La primera derivada del área total respecto de x , resulta:  xLx
dx
dA

2
1
8
1
Igualando a 0 y despejando el valor de x , queda:

 822
16


L
x
La segunda derivada del área total respecto de x queda: 0
2
1
8
1
2
2



dx
Ad
lo
que nos indica que es positiva ,x en consecuencia, el valor del área es un mínimo.
Reemplazando en x el valor de la longitud del alambre: 20 cm tenemos que x = 11,2 cm.
EJEMPLO 2: A un tanque que tiene la forma de un cono circular recto invertido de
4 m de radio y 16 m de altura entra agua a una razón de 50 cm3
/s. ¿A qué velocidad está
subiendo el nivel del agua cuando este se encuentra a 4 m. de altura? ¿A qué velocidad está
cambiando el radio en ese mismo instante?
SOLUCIÓN
En la figura aparece el cono con las dimensiones dadas y una porción del volumen en
cualquier instante t .
Desígnese por:
 :V volumen (en cm3
) de agua en el tanque en el instante t (s).
 :x Radio (en cm) de la sección del cono al nivel del líquido en el instante t .
 :y Altura del agua (en cm) en el instante t .
Datos: 






seg
cm
dt
dV 3
50

El volumen del agua en el instante t viene dado por:
 1
3
1 2
yxV 
De la semejanza de los triángulos ODE y OBC, se deduce que:
 
 






3
4
24
4
16
y
x
xy
x
y
Puede formularse la pregunta así:
?
dt
dy
cuando y = 4 m = 400 cm.
Una manera simple de calcular
dt
dy
consiste en expresar V en  1 en términos
únicamente de la variable y (usando  3 ) y derivando en ambos lados con respecto a .t
Así,
3
2
2
4843
1
3
1
yy
y
yxV








dt
dyy
dt
dy
y
dt
dV





16
3
48
2
2
De donde
2
16
y
dt
dV
dt
dy



De acuerdo a las condiciones del problema:
 
 5
200
1
400
5016
2
3











s
cm
cm
s
cm
dt
dy
Indicando con esto que la altura crece a esa velocidad.
b. Puede formularse la pregunta así:

?
dt
dx
cuando y = 4 m. = 400 cm.  x = 100 cm.
Una manera sencilla de encontrar la solución, consiste en derivar ambos miembros de
 3 con respecto a .t .
Así,
 6
800
1
200
1
4
1
4
1





















s
cm
s
cm
dt
dy
dt
dx
Indicando con esto que el radio crece a esta velocidad.
Otra manera de obtener la solución, consiste en expresar V en  1 en términos
únicamente de la variable x (usando  2 ) y derivar en ambos lados con respecto a
t .(¡VERIFIQUE!)
EJEMPLO 3: Se dispone de una cartulina cuadrada de lado a y se quiere hacer una
caja sin tapa recortando cuadrados iguales en las esquinas y doblando sus lados. ¿Cuál debe
ser la longitud del lado del cuadrado que se recorta para que el volumen de la caja sea
máximo? ¿Cuál es el volumen de la caja?
SOLUCIÓN:
Sea :x Longitud del lado del cuadrado que se recorta en cada una de las esquinas
según la figura de abajo en la parte (a)), donde .
2
0
a
x 
(a) (b)

Al doblar la parte de cartulina restante, se forma la caja abierta que aparece en la
figura de arriba en la parte (b).
Ahora, volumen de la caja = área de la base x altura. Esto es,
     1
2
0;442 2232 a
xxaaxxxxaxV 
Puesto que  xV (FUNCIÓN A MAXIMIZAR) es una función continua en el
intervalo ,
2
,0 


 a
entonces  xV alcanza un valor máximo y un valor mínimo en dicho
intervalo.
Al derivar  xV en  1 e igualar a cero, se obtienen los puntos críticos. En efecto:
     062812 22
 x-ax-aaaxxxV
De acá:









6
06
2
02
a
xax
ó
a
xax
Son los puntos críticos
Para analizar la naturaleza de los puntos críticos, se usa el criterio de la segunda
derivada. Así,
  axxV 824 
Luego:
04
2
8
2
1624
8
2
24
8
2
24
2













 a
aaa
a
a
a
aa
V
Lo cual indica que
2
a
x  corresponde a un mínimo relativo. (Interprete
geométricamente el resultado).

04
6
24
6
4824
8
6
24
8
6
24
6















 a
aaa
a
a
a
aa
V
Lo cual indica que
6
a
x  corresponde a un máximo relativo.
En consecuencia, el volumen máximo se obtiene recortando en las esquinas de la
cartulina cuadrados de lado
6
a
y se obtiene de esta forma una caja cuyo volumen viene
dado por:
27
2
69
4
63
2
63
3
6366
2
6
322222
aaaaaaaaaa
a
aa
a
a
V 


































 






























EJERCICIOS:
1. Utilice el criterio de la segunda derivada para encontrar los extremos de las
funciones indicadas:
a)   732 2
x+x=xf  b)    3
1x=xf c)  
x
=xxf
1

SOLUCIÓN: a)
8
47
4
3






f MÍNIMO. b) No existen extremos. c)   21 f
MÍNIMO;   21 f MÁXIMO.
2. ¿Cuáles son las dimensiones de un campo rectangular de área dada que requiere la
menor cantidad de cercado?
SOLUCIÓN: Un cuadrado
3. Encuentre el volumen de la mayor caja que se puede construir de un cuadrado de
cartón de 20 cm de lado cortando cuadros iguales en cada esquina y doblando los
lados hacia arriba.
SOLUCIÓN: V =
27
16
592 cm2

APLICACIONES DE LA DERIVADA A LA FÍSICA
VELOCIDAD Y ACELERACION:
dt
ds
v(t)  ,
  2
2
dt
sd
dt
dv
ta 
EJEMPLO: Un punto se mueve a lo largo de un eje coordenado horizontal de tal
manera que su posición en el instante t está especificado por: ,30366 23
t-tts  s se mide
en pies y t en segundos.
a) ¿Cuándo la velocidad es cero?
b) ¿Cuándo la velocidad es positiva?
c) Cuándo el punto se está moviendo hacia la izquierda (es decir, en la dirección
negativa).
d) ¿Cuando la aceleración es positiva?
SOLUCIÓN:
a)   .62336123 2
 tttt
dt
ds
v Así 0v en 2t y .6t
b) ,0v cuando    .062  tt La soluciones 2t o ,t 6 en notación de
intervalo    .62  ,,
c) El punto está moviéndose hacia la izquierda cuando ,0v esto es cuando
   .062  tt Esta desigualdad tiene como solución el intervalo .62,
d)  .tt
dt
dv
a 46246  Por tanto 0a cuando .t 4
EJERCICIOS DE APLICACIONES DE LA DERIVADA A LA FÍSICA
1. Un objeto que se lanza directamente hacia arriba está a una altura 2564816 2
 tts
pies después de t segundos:
a. ¿Cuál es su velocidad inicial?
b. ¿Cuándo alcanza su altura máxima?
c. ¿Cuál es su altura máxima?
d. ¿Cuándo llega al suelo?

e. ¿Con qué rapidez llega al suelo?
2. Un objeto lanzado directamente hacia arriba desde el nivel del piso con una velocidad
de 48 pies por segundos, está aproximadamente a tts 4816 2
 pies de altura al final
de t segundos.
a. ¿Cuál es la altura máxima?
b. Al final de un segundo, ¿Qué tan rápido se está moviendo el objeto, y en qué
dirección?
c. ¿Cuánto tarda en regresar a su posición original?
3. Un proyectil se dispara directamente hacia arriba desde el suelo, con una velocidad
inicial de v0 pies por segundos. Su altura a los t segundos está dada por 2
0 16ttvs 
pies. ¿Cuál debe ser su velocidad inicial para que el proyectil alcance una altura
máxima de 1 milla?
4. Se lanza verticalmente una pelota hacia arriba con una velocidad inicial v0=30 metros
por segundo. si la ecuación del movimiento es  
2
2
0
gt
tvts  con ;10 2
s
m
g  hallar.
a. La velocidad de la pelota en un tiempo t .
b. La velocidad en t = 1 s, t =3s.
c. El tiempo que tarda en alcanzar la altura máxima.
d. La altura máxima de la pelota.
e. La velocidad que lleva la pelota al llegar de nuevo al suelo.
ANEXO I. APLICACIÓN DE LA DERIVADA AL CÁLCULO DE LÍMITES
Los límites de formas indeterminadas que no pueden resolverse mediante la
factorización, generalmente se resuelven por la conocida en la matemática como Regla de
L´Hôpital, que contiene en su estructura el concepto de derivada.
TEOREMA DE L´HÔPITAL
Supongamos que las funciones f y g están definidas y son derivables en cierto
entorno de a . Si 

)(lim xf
ax
0)(lim 

xg
ax
, y 0)( xg en cierto entorno de a , entonces, si
existe
)(
)(
lim
xg
xf
ax 


(finito o infinito), existe también
)(
)(
lim
xg
xf
ax
, y se cumple que:
)(
)(
lim
xg
xf
ax
=
)(
)(
lim
xg
xf
ax 


.
La Regla de L´Hôpital también es válida en el caso que las funciones f y g no están
definidas en a , pero 

)(lim xf
ax
0 y 0)(lim 

xg
ax
.

Si 0)()(  agaf , y )(xf  y )(xg satisfacen las condiciones puestas sobre las
funciones f y g , podemos aplicar la Regla de L´Hôpital a
)(
)(
cg
cf


, y obtenemos:
)(
)(
lim
xg
xf
ax 


=
)(
)(
lim
xg
xf
ax 


; aplicar sucesivamente.
EJEMPLO 1: Calcular:
ee
xx
xx 


ln1
lim
2
1
SOLUCIÓN:
En este caso estamos ante la indeterminación
0
0
, pues
0011)ln1(lim 22
1


xx
x
, y 0)(lim 1
1


eeeex
x
Resolvemos aplicando la Regla de L´Hôpital:



 ee
xx
xx
ln1
lim
2
1



 )(
)ln1(
lim
2
1 ee
xx
xx ee
x
x
xx
3
1
2
lim
1



CÁLCULO DE LÍMITES DE LA FORMA


El teorema anterior es válido si se sustituye la exigencia de 

)(lim xf
ax
)(lim xg
ax
=0
por 

)(lim xf
ax
)(lim xg
ax
= , y se llama, por extensión, Regla de L´Hôpital.
EJEMPLO 2: Hallar:
x
x
x 1
ln
lim
0

SOLUCIÓN:
En este caso estamos ante la indeterminación


, pues, 

x
x
lnlim
0
, y

 xx
1
lim
0
. Resolvemos aplicando la Regla de L´Hôpital:

 










x
x
x
1
ln
lim
0
= 0lim
1
1
lim
2
0
2
0



 x
x
x
x
xx
Existen otras formas indeterminadas, 0.  e  , que pueden transformarse en las
formas
0
0
ó


, y aplicar la Regla de L´Hôpital.
Si queremos calcular )().(lim xgxf
ax
y, 0)(lim 

xf
ax
y 

)(lim xg
ax
, entonces,
)().( xgxf =
)(
1
)(
xg
xf
, y por tanto, )().(lim xgxf
ax
=
)(
1
)(
lim
xg
xf
ax
, y ahora es de la forma
0
0
.
Además, )().( xgxf =
)(
1
)(
xf
xg
, y es un límite de la forma


.
En dependencia del límite que se esté calculando, se hará una u otra de las
transformaciones anteriores, siguiendo el criterio que la aplicación de la Regla de L´Hôpital
simplifique el proceso de determinación del límite.
EJEMPLO 3: Calcular: 22
0
lnlim xx
x
SOLUCIÓN:
Observemos que 0lim 2
0


x
x
, y 

2
0
lnlim x
x
Luego, estamos ante una
indeterminación del tipo 0..
Transformando,
22
0
lnlim xx
x
= 

2
2
0 1
ln
lim
x
x
x
  









2
2
0
1
ln
lim
x
x
x



4
2
0 2
2
lim
x
x
x
x
x
0lim 2
0


x
x

Observe que 22
0
lnlim xx
x
=
2
2
0
ln
1
lim
x
x
x
, pero esta transformación es menos
recomendable en este caso en particular, pues la derivada de 2
ln
1
x
es mucho más compleja
que, simplemente, la derivada de 2
ln x .
EJERCICIOS:
CALCULAR SOLUCIÓN (JUSTIFICA LOS PASOS)
1. 30
lim
x
xsenx
x




 20 3
cos1
lim
x
x
x 6
1
lim
6
1
6
)(
lim
00


 x
xsen
x
xsen
xx
2.
34
23
lim 23
23
1 

 xx
xx
x 5
3
83
63
83
63
lim 2
2
1






 xx
xx
x
3.
x
x
sen
x 1
4
lim

4 41.4)
4
(coslim 
 xx
4. xx e
x2
lim


 xx e
x2
lim 0
2
lim 
 xx e
5. 






 xxx ln
1
1
1
lim
1









 xx
xx
x ln)1(
1ln
lim
1
=















x
xx
x
x 1
).1(ln.1
1
1
lim
1
=

















2
2
1 )1(1
1
lim
x
xx
x
x
x















2
2
1 1
1
lim
x
x
x
x 2
1
1
1
lim
1








 xx
.
TEOREMA DE ROLLE Y TEOREMA DEL VALOR MEDIO
TEOREMA DE ROLLE: Sea f una función de variable real que satisface las
siguientes propiedades:
i. f es continua en el intervalo cerrado  .,ba
ii. f es derivable en el intervalo abierto  .,ba
iii.     .0 bfaf

Entonces, existe por lo menos un punto  bac , tal que:   .0 cf
El siguiente teorema que se enuncia y se demuestra a continuación, es una
generalización del teorema de Rolle y se conoce con el nombre del teorema del valor medio
para derivadas.
TEOREMA DEL VALOR MEDIO: Sea f una función de variable real que
satisface las siguientes propiedades:
i. f es continua en el intervalo cerrado  .,ba
ii. f es derivable en el intervalo abierto  .,ba
Entonces, existe por lo menos un punto  bac , tal que:      .
ab
afbf
cf



REFERENCIAS BIBLIOGRÁFICAS
Larson, Hostetler, Edwards: Cálculo. Volumen 1 y 2. Editorial McGraw-Hill. 6ta. Ed.
Leithold. L: El Cálculo. Oxford University Press. 7ma. Ed.
Purcell, E: Cálculo con Geometría Analítica. Editorial Prentice-Hall-Hispanoamericana.
8va. Ed.
Saenz, J. (1995). Cálculo Diferencial para ciencias e ingeniería. Primera Edición.
Hipotenusa Barquisimeto- Venezuela.
Tom Apóstol. (2005). Calculus. Cálculo con funciones de varias variables y álgebra lineal,
con aplicaciones a las ecuaciones diferenciales y a las probabilidades. Editorial
Reverté.
"Si he llegado a ver más lejos que otros, es porque me subí a hombros de gigantes"
Sir. Isaac Newton

Aplicaciones de la derivada: recta tangente, normal, máximos y mínimos

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Similar a Aplicaciones de la derivada: recta tangente, normal, máximos y mínimos

Similar a Aplicaciones de la derivada: recta tangente, normal, máximos y mínimos (20)

Más de Julio Barreto Garcia

Más de Julio Barreto Garcia (20)

Último

Último (20)

Aplicaciones de la derivada: recta tangente, normal, máximos y mínimos