Este documento describe el proceso de carga y descarga de un condensador. Explica que un condensador almacena energía eléctrica entre sus placas y que su capacidad depende de factores como el área, distancia y material dieléctrico entre las placas. Detalla las ecuaciones que rigen estos procesos y los pasos experimentales para medir la capacidad de un condensador y determinar la constante de tiempo en cada caso. El objetivo es estudiar cómo varía el voltaje con el tiempo en un circuito RC y comprender el funcionamiento bás

1. 1
CARGA Y DESCARGA DE UN CONDENSADOR
1. OBJETIVOS
1 Estudio de la carga y la descarga de un condensador y medida de su capacidad.
2 Comprender el funcionamiento de los capacitores.
3 Estudiar como varia el voltaje y la corriente en un circuito RC.
4 Determinar experimentalmente la constante de tiempo = RC , para un circuito RC.
5 Observar la in
uencia de los materiales dielectricos, caractersticas como el area y distancia entre las
placas.
2. MATERIALES
Figura 1: Conductores de cocodrilo
Figura 2: Fuente de alimentacion

2. LABORATORIO V FISICA III 2
Figura 3: Plaqueta de conexion
Figura 4: Voltmetro
Figura 5: Cronometro
Figura 6: capacitor
3. FUNDAMENTO TEORICO
Un capacitor esta formado por dos conductores separados por un medio material no conductor. Idealmente el
capacitor almacena energa electrica en forma de campo electrico entre los conductores. Cada conductor recibe el
nombre de electrodo, cuando a uno de los electrodos se agrega una carga electrica, en el otro se induce la misma
15 de octubre de 2014 Ing. Civil

3. LABORATORIO V FISICA III 3
cantidad pero de signo distinto, estableciendose un campo electrico. Si se aumenta la carga en el capacitor,
la diferencia de potencial entre sus electrodos se incrementa en forma proporcional. La relacion entre la carga
total Q en uno de sus electrodos y la diferencia de potencial V entre los electrodos es siempre una constante
denominada capacidad del elemento, que se expresa como:[1]
C =
Q
V
La capacidad C se expresa en faradios. La capacidad de un capacitor depende de la geometra de los conductores
que forman las placas del capacitor y del medio material que las separa.
Mientras mayor sea la permitividad, mayor es la capacidad del condensador electrico.
La capacitancia de un condensador esta dada por la formula: C = Er(A=d)
Donde:
- C = capacidad
- Er = permitividad
- A = area entre placas
- d = separacion entre las placas
La unidad de medida es el faradio. Hay submultiplos como el miliFaradio (mF), microFaradio(uF),
elnanoFaradio(nF) y elpicoF aradio(pF).
Las principales caractersticas electricas de un condensador son su capacidad o capacitancia y su maxima
tension entre placas (maxima tension que es capaz de aguantar sin da~narse).
3.1. DIELECTRICO O AISLANTE DEL CONDENSADOR ELECTRICO
Un dielectrico o aislante es un material que evita el paso de la corriente, y su funcion es aumentar la
capacitancia del capacitor. Los diferentes materiales que se utilizan como dielectricos tiene diferentes grados de
permitividad (diferente capacidad para el establecimiento de un campo electrico.[5]
Figura 7: tabla 1
3.2. CARGA DE UN CONDENSADOR
Considerese el circuito representado en la

4. gura

5. gura 8. Al cerrar el interruptor S, el condensador C empieza
a cargarse a un ritmo variable, cada vez mas lento, el cual depende del valor de R. Para deducir la formula que
rige el proceso de carga, vamos a aplicar las leyes de Kirchho a este circuito.
Figura 8: Se experimenta con la carga de un condensador C a traves de una resistencia R.
En la

6. gura 2 se indican los nudos (A y B) y las intensidades (I1, I2, e I3) que consideraremos en el circuito
para aplicar las leyes de Kirchho sobre las mallas. RV = (11; 10 0; 02)M
es la resistencia interna del
15 de octubre de 2014 Ing. Civil

7. LABORATORIO V FISICA III 4
voltmetro. Denotaremos por que la carga del condensador. Aplicando la primera ley de Kircho al nudo A se
tiene:
i) Nudo A:
[]I = I1 + I2 =
dq
dt
+ I2 (1)
Teniendo en cuenta ahora la segunda ley de Kirchho aplicada a la malla formada por la fuente de tension
E, la resistencia R y el condensador C, se tiene:
ii) Malla 1:
[]E = RI +
q
c
(2)
Figura 9: Equivalente al circuito electrico de la

8. gura 8
Donde: Se considera que el voltmetro posee una resistencia interna RV 1. y aplicada a la malla 2
formada por el condensador C y la resistencia del voltmetro RV , se obtiene:
iii) Malla 2:
[]
q
C
= I2RV (3)
Sustituyendo ahora la ecuacion (1) en la ecuacion (2) se obtiene:
E = R(
dq
dt
+ I2) +
q
C
(4)
y teniendo en cuenta (3):
E = R
dq
dt
+
R
RV
q
C
+
q
C
= R
dq
dt
+ (1 +
R
RV
)
q
C
(5)
Por tanto, reordenando, la ecuacion diferencial que hay que integrar es la siguiente:
dq
CE (1 + R
RV
)q
=
1
RC
dt (6)
La condicion inicial que impondremos en el experimento sera que el condensador este descargado antes de cerrar
el interruptor. Para que la ecuacion (6) cumpla esta condicion de contorno, basta hacer
para t = 0
q = 0; V = 0 (7)
De modo que integraremos la ecuacion anterior entre t = 0 y un instante cualquiera t en el que la carga es q, es
decir: Z q
0
dq
CE (1 + R
RV
)q
=
1
RC
Z t
0
t (8)
Si efectuamos la integracion, y tomamos el antilogaritmo del resultado, queda:
q =
CE
1 + R
RV
(1 e
1+ R
RV
RC t) (9)
15 de octubre de 2014 Ing. Civil

9. LABORATORIO V FISICA III 5
la cual, haciendo R0 = RRV
R+RV
y
S = R0C (10)
se puede escribir del siguiente modo:
q =
R0
R
CE(1 e t
S ) (11)
y por tanto la variacion del voltaje con el tiempo resulta ser:
V =
q
C
=
R0
R
E(1 e t
S ) = Vmax(1 e t
S ) (12)
La magnitud S de

10. nida en (10) tiene dimensiones de tiempo y, de hecho, su valor se utiliza como indicativo del
tiempo que tarda en cargarse el condensador (tiempo de subida de la carga, en ingles rise-time). Estrictamente,
el tiempo de carga es in

11. nito dado el caracter asintotico del termino con exponencial en (12), y el valor de V
cuando el condensador esta completamente cargado es el que tomara si no hubiese condensador en el circuito,
es decir,
V(t!1) = Vmax =
R0
R
E =
1
1 + R
RV
E (13)
En la practica, se alcanza un valor experimental indistinguible de (13) en un tiempo razonable (dependiendo de
los valores de R y de RV ).
3.3. DESCARGA DE UN CONDENSADOR
Si, estando cargado el condensador hasta un potencial V0, se abre el interruptor, el condensador empieza a
descargarse a traves de la resistencia interna del voltmetro, RV = (11; 100; 02)M
(

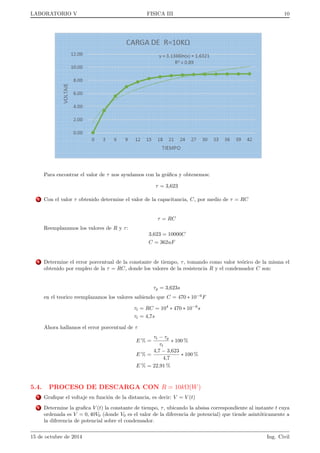
12. gura 3). Tomando esta
condicion inicial, es decir,
para t = 0
V = V0; q = q0 =
V0
C
(14)
y siguiendo pasos analogos a los del apartado 3.2. , se puede demostrar que el potencial disminuye con el tiempo
Figura 10: Esquema del circuito electrico que ilustra la descarga de un condensador de capacidad C a traves de
la resistencia ohmica RV del voltmetro.
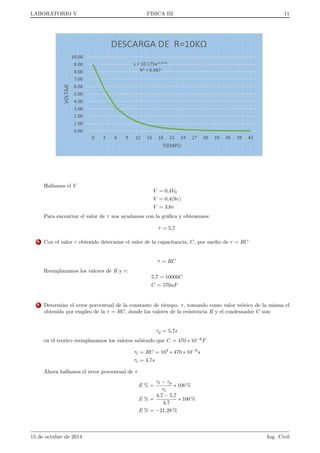
de acuerdo con la ecuacion:
V = V0e t
d ; d = RV C (15)
el tiempo S ahora es el tiempo en el que el potencial (o la carga) cae en un factor e, es decir para t = S se
tiene V = V0
e y se llama tiempo de descarga o decaimiento (en ingles decay o fall-time).[4]
4. PROCEDIMIENTOS Y TOMA DE DATOS
1 Arme el circuito de la

13. gura :
2 Veri

14. que que el condensador esta completamente descargado conectando el voltmetro entre sus bornes,
en caso contrario, cierre el circuito conectando la punta P en el punto b para lograrlo.
3 Para hacer una serie de lecturas de diferencia de potencial, cierre el interruptor S y registre los valores
del voltmetro cada 10 segundos en una tabla, dado que el instrumento a utilizar es digital y muy preciso
es que se realizara solo una serie de lecturas.
4 Anote las lecturas del voltmetro en la siguiente tabla:
15 de octubre de 2014 Ing. Civil

15. LABORATORIO V FISICA III 6
Figura 11:
a) Para R = 4; 7k
(W)
b) Para R = 10k
(W)
5 Cuando el voltmetro mida el mismo valor mas de 20s (dos lecturas consecutivas), no haga mas lecturas.
6 Desarrollo de la experiencia del proceso de descarga. Arme el circuito de la