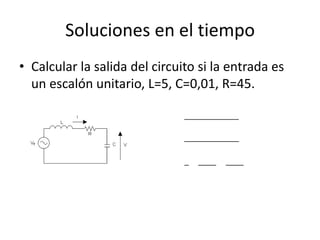
Este documento introduce conceptos fundamentales sobre la transformada de Laplace y funciones de transferencia para el análisis de sistemas de control automático. Explica propiedades básicas de la transformada de Laplace, transformadas comunes, funciones de transferencia y su relación con la entrada y salida de un sistema, y analiza la ubicación de polos y ceros para determinar la estabilidad de un sistema.

1. TRANSFORMADA DE LAPLACE Y
FUNCIONES DE TRANSFERENCIA
CONTROL AUTOMATICO I – CAS6201

2. Propiedades de Laplace
𝑑𝑥(𝑡)
𝐿 = 𝑠𝑋 𝑠 − 𝑥 0 Primera derivada
𝑑𝑡
𝑑 2 𝑥(𝑡)
𝐿 2 = 𝑠 2 𝑋 𝑠 − 𝑠𝑥 0 − 𝑥 (0) Segunda derivada
𝑑𝑡
𝐿 𝑥(𝑡)𝜇(𝑡 − 𝑡0 ) = 𝑒 −𝑠𝑡0 𝑋(𝑠) Retardo temporal
𝐿 𝑎𝑥 𝑡 + 𝑏𝑦(𝑡) = 𝑎𝑋 𝑠 + 𝑏𝑌(𝑠) Linealidad
𝑡
𝑋(𝑠)
𝐿 𝑥 𝑡 𝑑𝑡 = Integral
0 𝑠
c(𝑡) ∗ 𝑝(𝑡) = 𝐶 𝑠 𝑃(𝑠) Convolución

3. Transformadas Comunes
𝛿(𝑡) 1 𝑠
cos(𝑎𝑡)
𝑠 2 + 𝑎2
𝐴 𝑎
𝐴𝜇(𝑡) sen(𝑎𝑡)
𝑠 𝑠 2 + 𝑎2
1 𝑠+ 𝑎
𝑒 −𝑎𝑡 𝑒 −𝑎𝑡 cos(𝜔𝑡)
𝑠+ 𝑎 (𝑠 + 𝑎)2 +𝜔 2
𝜔
𝑒 −𝑎𝑡 𝑠𝑒𝑛(𝜔𝑡)
(𝑠 + 𝑎)2 +𝜔 2

4. Transformadas Comunes
• Calcular transformadas de las siguientes
señales:
𝑠 𝑡 = 𝑒 −13𝑡 + 10𝛿(𝑡) 𝑠 𝑡 ∗ 𝑞(𝑡)
𝑝 𝑡 = 8𝜇(𝑡) 𝑢 𝑡 ∗ 𝑞 𝑡 + 𝑣 𝑡 ∗ 𝑠(𝑡)
𝑞 𝑡 = 𝑒 𝑡/8 ′∗′ ∶ 𝐶𝑂𝑁𝑉𝑂𝐿𝑈𝐶𝐼Ó𝑁
𝑢 𝑡 = 7cos(2𝜋𝑡)
𝑣 𝑡 = 5sen(10𝜋𝑡)

5. Transformadas Comunes
• Calcular transformadas de los siguientes
sistemas:
𝑦 𝑡 = 3𝑦 𝑡 + 4𝑦 𝑡 + 𝑢(𝑡)
Be 𝑡 + 𝑒(𝑡) = 𝑢 𝑡 + 𝐶𝑢 − 𝐴𝑒

6. Funciones de Transferencia
• Transferencia es la relación existente entre la
salida y la entrada de un sistema
𝑌 = 𝐺(𝑈)
U Y
G

7. Funciones de Transferencia
• Divisor de Tensión:
𝑅2
𝑉 𝑜𝑢𝑡 = 𝑉
𝑅2 + 𝑅1 𝑖𝑛
𝑉𝑖𝑛 𝑅2 𝑉 𝑜𝑢𝑡
𝑉 𝑜𝑢𝑡 𝑅2 𝑅2 + 𝑅1
=
𝑉𝑖𝑛 𝑅2 + 𝑅1

8. Funciones de Transferencia
• Podemos entender una transferencia como
FUNCION, es decir:
𝑦 = 𝐻(𝑢)
• Por ejemplo:
U=2 Y = 13
𝐻 𝑢 = 5𝑢 + 3 H(u)

9. Funciones de Transferencia
• Se puede definir la Función de Transferencia
como:
𝐿*ℎ(𝑡)+ = 𝐻(𝑠)
𝑌(𝑠)
𝐻 𝑠 =
𝑈(𝑠)
• Siempre y cuando las condiciones iniciales sean
iguales a cero.

10. Funciones de Transferencia
• Respuesta a Impulso
– La transformada de Laplace de un impulso unitario es
1
– Entonces:
𝑌 𝑠 = 𝐻 𝑠 ⋅ 𝐿*𝛿(𝑡)+ = 𝐻(𝑠)
• Entonces la transformada de la respuesta a
impulso de un sistema lineal es el mismo sistema.

11. Funciones de Transferencia
• Determinar la salida “y” en función de “u” y
“p”.
p
+
u y
H
+
𝑦= 𝑝 + 𝐻(𝑢)

12. Polos y Ceros
• Polos: Son las raíces del denominador de una
función de transferencia.
• Ceros: Son las raíces del numerador de una
función de transferencia.
𝑏 𝑛 𝑠 𝑛 + 𝑏 𝑛−1 𝑠 𝑛−1 + ⋯ + 𝑏1 𝑠 + 𝑏0
𝑎 𝑛 𝑠 𝑛 + 𝑎 𝑛−1 𝑠 𝑛−1 + ⋯ + 𝑎1 𝑠 + 𝑎0

13. Polos
• La ubicación de los polos de una función de
transferencia en el plano “s” determina el
comportamiento del sistema que modela.
• Los polos ubicados en el semi plano izquierdo
(SPI) son siempre estables ya que a entradas
acotadas se obtienen salidas acotadas
mientras que en el semi plano derecho (SPD)
sucede al contrario.

14. Polos
Región Estable Región Región Inestable
Críticamente
Estable

15. Polos
𝐴
𝐴𝜇(𝑡)
𝑠
1
𝑒 −𝑎𝑡
𝑠+ 𝑎
𝑠 𝑠+ 𝑎
cos(𝑎𝑡) 𝑒 −𝑎𝑡 cos(𝜔𝑡)
𝑠 2 + 𝑎2 (𝑠 + 𝑎)2 +𝜔 2
𝑎 𝜔
sen(𝑎𝑡) 𝑒 −𝑎𝑡 𝑠𝑒𝑛(𝜔𝑡)
𝑠 2 + 𝑎2 (𝑠 + 𝑎)2 +𝜔 2

16. Polos
• Polos Reales: 𝐼𝑚
1
𝐻 𝑠 = 𝑐 X
(𝑠 + 𝑎)(𝑠 − 𝑏)
X X
−𝑎 𝑏 𝑅𝑒
X
• Polos Imaginarios: −𝑐
1
𝐻 𝑠 = 2
(𝑠 + 𝑐 2 )

17. Polos
• Polos Complejos conjugados:
𝐼𝑚
X 𝜔 𝑛 1 − 𝜉2
1 𝜔𝑛
𝐻 𝑠 = 2
(𝑠 + 2𝜉𝜔 𝑛 + 𝜔 𝑛 2 )
−𝜉𝜔 𝑛 𝑅𝑒
X −𝜔 𝑛 1 − 𝜉 2
𝑠1 = −𝜉𝜔 𝑛 + 𝜔 𝑛 1 − 𝜉 2
𝑠2 = −𝜉𝜔 𝑛 − 𝜔 𝑛 1 − 𝜉 2

18. Polos
• Diseñe “a” y “b” para que el sistema H sea
estable y tenga un polo en el origen.
• ¿Se puede decir que sea críticamente
estable?.
𝑠+ 𝑎
𝐻 𝑠 = 2
(𝑠 + 𝑎𝑠 + 𝑏)

19. Ejercicios
• Calcular los polos de los siguientes sistemas e
indicar si son inestables:
𝑦 𝑡 = 3𝑦 𝑡 + 4𝑦 𝑡 + 𝑢(𝑡)
Be 𝑡 + 𝑒(𝑡) = 𝑢 𝑡 + 𝐶𝑢 − 𝐴𝑒
• Calcular A,B y C para que al utilizar el segundo
sistema como entrada del primer sistema el
conjunto sea estable.

20. Soluciones en el tiempo
• Fracciones Parciales: La idea de este método matemático es
separar el denominador de una fracción en una suma de
fracciones mas simples.
• Se utilizan variables auxiliares para luego igualar los
coeficientes de cada orden de “s”.
𝑏 𝑛 𝑠 𝑛 + 𝑏 𝑛−1 𝑠 𝑛−1 + ⋯ + 𝑏1 𝑠 + 𝑏0 𝐴𝑠 + 𝐵 𝐶 𝐷
= 2 + + ⋯+
𝑎 𝑛 𝑠 𝑛 + 𝑎 𝑛−1 𝑠 𝑛−1 + ⋯ + 𝑎1 𝑠 + 𝑎0 𝑠 + 𝑐1 𝑠 + 𝑐0 𝑠 + 𝑐2 𝑠
• Notar que el orden utilizado en cada numerador del lado
derecho tiene siempre un grado menos que el denominador.

21. Soluciones en el tiempo
• Calcular la salida del circuito si la entrada es
un escalón unitario, L=5, C=0,01, R=45.
𝑉𝑓
𝑉𝑐 =
𝐿𝐶𝑠 2 + 𝑅𝐶𝑠 + 1
20
𝑉𝑐 =
𝑠(𝑠 2 + 9𝑠 + 20)
1 4 5
𝑉𝑐 = + −
𝑠 𝑠+5 𝑠+4
𝑣 𝑐 (𝑡) = 1 + 4𝑒 −5𝑡 − 5𝑒 −4𝑡

22. Soluciones en el tiempo
• Calcular la respuesta a impulso en el tiempo
𝑠−1
𝐻 𝑠 =
(𝑠 + 3)(𝑠 − 2)
𝐴 𝐵
𝑌 𝑠 = + 𝐴 𝑠−2 + 𝐵 𝑠+3 = 𝑠−1
𝑠+3 𝑠−2
4
𝐴= 4/5 1/5
𝐴+ 𝐵 =1 5 𝑌 𝑠 = +
3𝐵 − 2𝐴 = −1 1 𝑠+3 𝑠−2
𝐵=
5
4 −3𝑡 1 2𝑡
𝑦 𝑡 = 𝑒 + 𝑒
5 5

23. Soluciones en el tiempo
• Calcular la respuesta a impulso en el tiempo
𝑠+6
𝐻 𝑠 = 2
(𝑠 + 4𝑠 + 13)
(𝑠 + 2) + 4 𝜔
𝑌 𝑠 = 𝑒 −𝑎𝑡 𝑠𝑒𝑛(𝜔𝑡)
((𝑠 + 2)2 +9) (𝑠 + 𝑎)2 +𝜔 2
𝑠+ 𝑎
(𝑠 + 2) 4 3 𝑒 −𝑎𝑡 cos(𝜔𝑡)
+ ⋅ (𝑠 + 𝑎)2 +𝜔 2
((𝑠 + 2)2 +32 ) 3 ((𝑠 + 2)2 +32 )
4 −2𝑡
𝑦 𝑡 = 𝑒 −2𝑡 cos(3𝑡) + 𝑒 sin(3𝑡)
3

24. Recapitulación
• La estabilidad de un sistema se interpreta mediante la
ubicación de sus polos, pudiendo ser un sistema:
– Estable
– Críticamente Estable
– Inestable
• Las respuestas en el tiempo de los sistemas lineales se
pueden definir en distintas regiones del plano de
Laplace.
• Un sistema puede ser identificado mediante su
respuesta al Impulso.