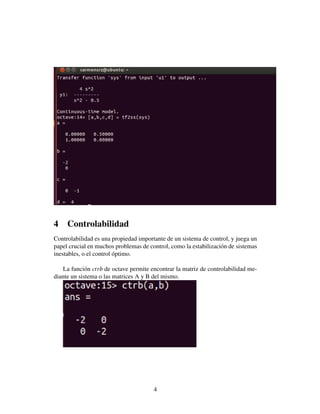
Este documento presenta un reporte sobre la automatización de un ventilador usando control de temperatura. Se utilizará un sensor de temperatura y variaciones de voltaje para aumentar o disminuir la potencia del ventilador dependiendo de la temperatura. Se describen la función de transferencia, representación en espacio de estados, controlabilidad, observabilidad y diagonalización del sistema.

1. Reporte de Automatizaci´ n
o
V´ ctor Briones (1441708)
o Carmen Suarez (1462633)
Osvaldo Hinojosa (1452344)
November 13, 2012
1 Introducci´ n
o
El objetivo de nuestro proyecto es controlar un ventilador tomando en cuenta la
temperatura, por medio de variaciones de voltaje que permiten aumentar o dis-
minuir la potencia del ventilador, bas´ ndose en la temperatura del lugar, si so-
a
brepasa una temperatura dada, la velocidad aumenta, en cambio si la temperatura
es menor la potencia del ventilador disminuye. En caso de que la temperatura sea
muy baja y no amerite que el ventilador se encuentre encendido, este permanecer´ a
apagado.
Se utilizar´ un sensor de temperatura para medir la temperatura del lugar, con
a
esto como entrada del sistema podemos saber que modificaciones se tendran que
realizar y as´ determinar si hay que aumentar o disminuir la potencia del venti-
ı
lador.
2 Funci´ n de transferencia
o
Para la funci´ n de transferencia se utiliza de ecuaci´ n de entrada la f´ rmula de la
o o o
ley de enfriamiento de Newton, donde la velocidad de enfriamiento de un cuerpo
en un ambiente fr´o cuya temperatura es T m es proporcional a la diferencia entre
ı
la temperatura instant´ nea del cuerpo y del ambiente. La ecuaci´ n es:
a o
dT
= −r(T − T m)
dt
dT
Y (s) = + (−r(T − T m))
dt
−r(T − T m)
Y (s) = sT (s) +
s
1

2. La ecuaci´ n de salida es una formula de potencia, la cual dice que esta es
o ´
directamente proporcional a la diferencia de potencia entre terminales y la inten-
sidad de corriente que pasa a trav´ s del dispositivo:
e
dw
p= IV
dt
X (s) = sW (s)IV
La funci´ n de transferencia a utiliz´ r despues de sustituir las ecuaciones es la
o a
siguiente:
sW (s)IV
G(s) =
sT (s) + −r(T s m)
−T
2.1 Diagrama de bloques
La entrada es la temperatura que haya en el lugar T (s) y la salida es la velocidad
del ventilador S(s).
Diagrama de bloques
−r(T −Tm )
sT (s)+
T (s) s S(s)
sW (s)IV
Utilizando algebra de bloques
−r(T −Tm )
T (s) sT (s) + s
S(s)
−
sW (s)IV
2

3. Diagrama final
T (s) sT (s) S(s)
−r(T −Tm )
− s
sW (s)IV
3 Reprecentaci´ n en espacio de estados
o
La representaci´ n de la funci´ n de transferencia en un espacio de estados es la
o o
siguiente:
Y (s) b0 sn + b1 sn−1 + ... + bn−1 s + bn
= n
U (s) s + a1 sn−1 + ... + an−1 s + an
Transformando nuestra funci´ n de transferencia, aplicando algunas propiedades
o
queda la siguiente funci´ n:
o
Y (s) 120s2 4s2
= = 2
U (s) 30s2 − 15 s − 0.5
Utilizando la representaci´ n en un espacio de estados con nuestra funci´ n de
o o
transferencia:
Y (s) b0 s n
= n
U (s) s − an
Donde:
• b0 = 4
• a1 = 0
• a2 = −0.5
3

4. 4 Controlabilidad
Controlabilidad es una propiedad importante de un sistema de control, y juega un
papel crucial en muchos problemas de control, como la estabilizaci´ n de sistemas
o
inestables, o el control optimo.
´
La funci´ n ctrb de octave permite encontrar la matriz de controlabilidad me-
o
diante un sistema o las matrices A y B del mismo.
4

5. 4.1 Forma Canonica Controlable
La forma canonica controlable tiene la forma:
Por lo cual la ecuaci´ n de nosotros queda de la siguiente manera:
o
x′ (t)
1 0 1 x1 (t) 0
= + u(t)
x′ (t)
2 0.5 0 x2 (t) 1
x1 (t)
y(t) = 2 0 + 4u(t)
x2 (t)
5 Observabilidad
Observabilidad es una propiedad importante de un sistema de control, y gobierna
la existencia de una soluci´ n de control ptimo. Es una medici´ n que determina
o o
c´ mo los estados internos pueden se inferidos a trav´ s de las salidas externas.
o e
La funci´ n obsv de octave permite encontrar la matriz de controlabilidad me-
o
diante un sistema o las matrices A y C del mismo.
5

6. 5.1 Forma Canonica Observable
La forma canonica observable tiene la forma:
Por lo cual la ecuaci´ n de nosotros queda de la siguiente manera:
o
x′ (t)
1 0 0.5 x1 (t) 2
′ (t) = 1
x2 0 x2 (t)
+
0
u(t)
x1 (t)
y(t) = 0 1 + 4u(t)
x2 (t)
6 Diagonalizaci´ n
o
Diagonalizar una matriz A significa encontrar dos matrices tales que:
A = PDP−1
Donde la matriz P se le conoce como matriz de paso y la matriz D es una
matriz diagonal, ambas son del mismo tamao que la matriz A. La matriz P−1 es la
inversa de P.
Se calculan los eigenvalores y eigenvectores de la matriz A para poder hallar
la matriz de paso y la matriz diagonal. La matriz de paso tiene n columnas, cada
una de ellas est formado por los eigenvectores de la matriz A, la primera contiene
el primer eigenvector, la segunda el segundo eigenvector y as sucesivamente. La
matriz D es una matriz diagonal cuyos elementos en la diagonal son los eigenval-
ores correspondientes a los eigenvectores que se tomaron para construir la matriz
P, el primer elemento en la diagonal corresponde al primer eigenvalor del primer
eigenvector, el segundo elemento corresponde al segundo eigenvector y as sucesi-
vamente. Una vez construida la matriz P se calcula su inversa.
6

7. 6.1 Forma Can´ nica Diagonal
o
La forma can´ nica diagonal es representada de la siguiente manera:
o
Para obtener la ecuaci´ n primero sacamos las races del denominador con la
o
funci´ n residuo de octave, lo que sale en a son las races y lo que sale en b es el
o
resultado de las fracciones parciales.
7

8. Con eso queda:
Y (s) 1.4142 1.4142
= +
U (s) s − 1 s + 1
2 2
Donde:
• c1 = 1.4142
• c2 = −1.4142
1
• p1 = 2
1
• p2 = − 2
La ecuaci´ n final queda:
o
1
x′ (t) 2 0 x1 (t) 1
1 = + u(t)
x′ (t)
2 0 1 x2 (t) 2
2
x1 (t)
y(t) = 1.4142 −1.4142 + 4u(t)
x2 (t)
8