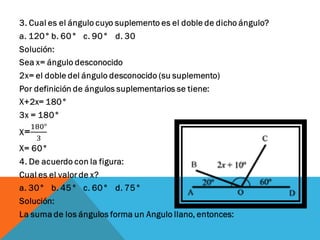
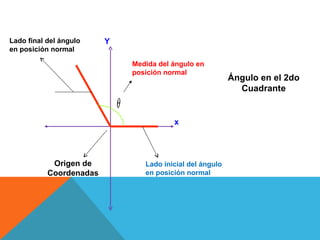
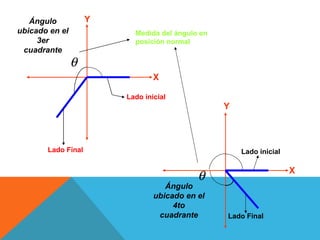
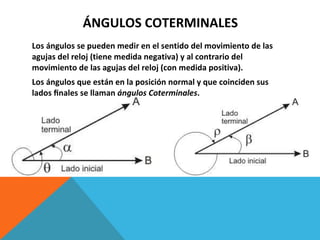
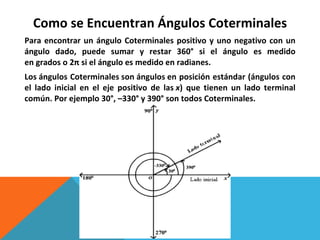
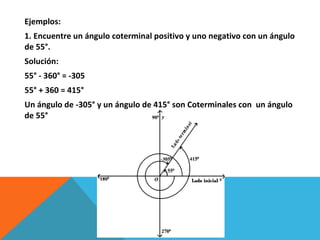
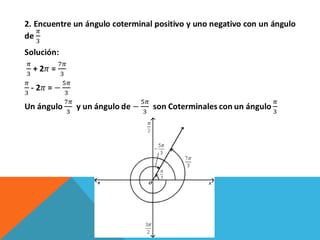
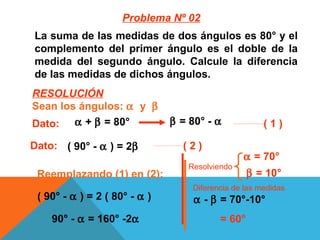
Este documento describe conceptos relacionados con ángulos como ángulos orientados, ángulos en posición normal y ángulos coterminales. Explica que los ángulos coterminales son ángulos en posición estándar que tienen el mismo lado terminal. Para encontrar ángulos coterminales de un ángulo dado, se suma o resta 360 grados o 2π radianes al ángulo. También presenta dos ejemplos resueltos de problemas relacionados con ángulos.

1. CONCEPTO DE ÁNGULO, ÁNGULOS ORIENTADOS, ÁNGULOS EN POSICIÓN NORMAL Y ÁNGULOS COTERMINALES . DOCENTE: ELKIN GUILLEN ÁLVAREZ 2011

2. ÁNGULOS

3. CLASIFICACIÓN DE ÁNGULOS Por su magnitud:

5. Por su posición:

6. Veamos algunos ejemplos:

7. 1. Cuál es el complemento de 75°? a. 180° b. 25° c. 90° d. 15° Solución: Se x= complemento de 75° Por definición de ángulos complementarios: X+75° = 90° X= 90°-75° X= 15° 2. Según la figura: Cual es el valor de x? a. 15° b. 35° c. 180° d. 360° Los ángulos son complementarios si: X+55°+20= 90° X= 90°-55°-20° X=15°

10. x Y Lado inicial del ángulo en posición normal Lado final del ángulo en posición normal Medida del ángulo en posición normal Ángulo en el 2do Cuadrante Origen de Coordenadas

11. Y X Lado inicial Lado Final Medida del ángulo en posición normal Ángulo ubicado en el 3er cuadrante X Y Lado inicial Lado Final Ángulo ubicado en el 4to cuadrante

12. ÁNGULOS COTERMINALES Los ángulos se pueden medir en el sentido del movimiento de las agujas del reloj (tiene medida negativa) y al contrario del movimiento de las agujas del reloj (con medida positiva). Los ángulos que están en la posición normal y que coinciden sus lados finales se llaman ángulos Coterminales .

13. Como se Encuentran Ángulos Coterminales Para encontrar un ángulo Coterminales positivo y uno negativo con un ángulo dado, puede sumar y restar 360° si el ángulo es medido en grados o 2π si el ángulo es medido en radianes. Los ángulos Coterminales son ángulos en posición estándar (ángulos con el lado inicial en el eje positivo de las x ) que tienen un lado terminal común. Por ejemplo 30°, –330° y 390° son todos Coterminales.

14. Ejemplos: 1. Encuentre un ángulo coterminal positivo y uno negativo con un ángulo de 55°. Solución: 55° - 360° = -305 55° + 360 = 415° Un ángulo de -305° y un ángulo de 415° son Coterminales con un ángulo de 55°

17. PROBLEMAS RESUELTOS

18. El complemento de la diferencia entre el suplemento y el complemento de un ángulo “X” es igual al duplo del complemento del ángulo “X”. Calcule la medida del ángulo “X”. 90 - { ( ) - ( ) } = ( ) 180° - X 90° - X 90° - X 2 90° - { 180° - X - 90° + X } = 180° - 2X 90° - 90° = 180° - 2X 2X = 180° X = 90° RESOLUCIÓN Problema Nº 01 La estructura según el enunciado: Desarrollando se obtiene: Luego se reduce a:

19. La suma de las medidas de dos ángulos es 80° y el complemento del primer ángulo es el doble de la medida del segundo ángulo. Calcule la diferencia de las medidas de dichos ángulos. Sean los ángulos:  y   +  = 80° Dato:  = 80° -  ( 90° -  ) = 2  Reemplazando (1) en (2): ( 90° -  ) = 2 ( 80° -  ) 90° -  = 160° -2   = 10°  -  = 70°-10° = 60° Problema Nº 02 RESOLUCIÓN Dato: Diferencia de las medidas Resolviendo ( 1 ) ( 2 )  = 70°

20. Muchas gracias Prof. Elkin Guillen [email_address]