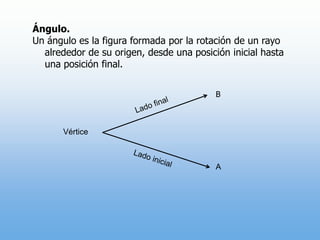
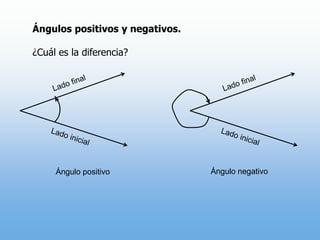
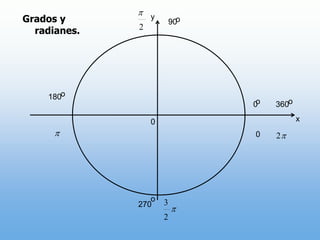
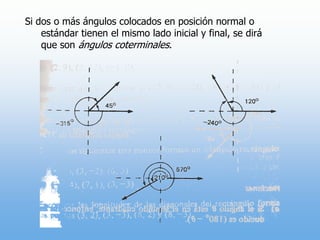
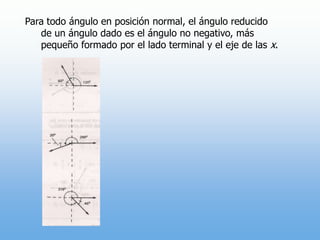
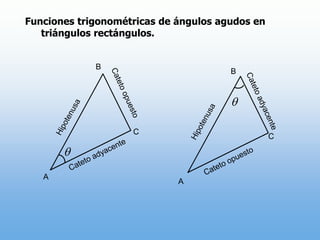
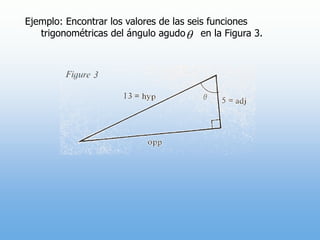
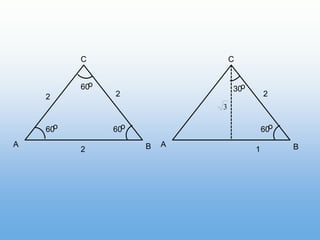
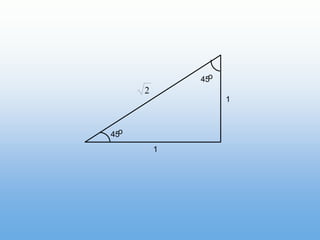
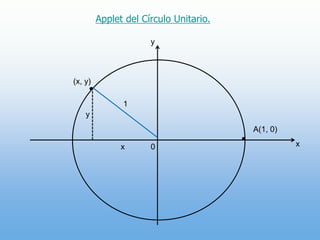
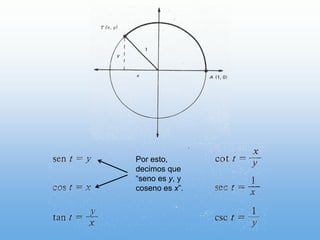
Un ángulo se forma por la rotación de un rayo alrededor de su origen. Puede ser positivo o negativo dependiendo de la dirección de la rotación. Se mide en grados y radianes, donde 90 grados equivale a π/2 radianes. Los ángulos coterminales tienen el mismo lado inicial y final.

1. Ángulo.Un ángulo es la figura formada por la rotación de un rayo alrededor de su origen, desde una posición inicial hasta una posición final.BLado finalVérticeLado inicialA

2. Ángulos positivos y negativos.¿Cuál es la diferencia?Lado finalLado finalLado inicialLado inicialÁngulo negativoÁngulo positivo

3. yoGrados y radianes.90o180oo0360x00o270

4. Para cambiar de radianes a grados se multiplica porPara cambiar de grados a radianes se multiplica porEjemplos: Convierte en radianes los siguientes ángulos.Ejemplos: Convierte en grados los siguientes ángulos.

5. Un ángulo está en posición normal o estándar cuando su vértice y el lado inicial coinciden con el origen y el lado positivo del eje x respectivamente, en un sistema de coordenadas.

6. Si dos o más ángulos colocados en posición normal o estándar tienen el mismo lado inicial y final, se dirá que son ángulos coterminales.

7. Para todo ángulo en posición normal, el ángulo reducido de un ángulo dado es el ángulo no negativo, más pequeño formado por el lado terminal y el eje de las x.

8. Grados, minutos y segundos.Ejemplos:1. Expresar la medida 72 13’59’’ como un decimal.2. Expresar el ángulo 173.372 en grados, minutos y segundos.oo

9. Funciones trigonométricas de ángulos agudos en triángulos rectángulos.BBCateto opuestoCateto adyacenteHipotenusaHipotenusaCCCateto adyacenteCateto opuestoAA

10. Funciones trigonométricas de ángulos agudos en triángulos rectángulos.

11. Ejemplo: Encontrar los valores de las seis funciones trigonométricas del ángulo agudo en la Figura 3.

12. CCoo6030222ooo606060AABB21

13. o451o451

14. O también:000002

15. Applet del Círculo Unitario.y(x, y)1yA(1, 0)x0x

16. Por esto, decimos que “seno es y, y coseno es x”.