Este documento presenta conceptos básicos sobre variables aleatorias discretas. Explica que una variable aleatoria discreta es aquella cuyo soporte es un conjunto contable. Define la función de distribución de probabilidades y el histograma de probabilidades. También introduce conceptos como la media, la varianza y el sesgo de una variable aleatoria, y cómo estos valores cambian cuando se aplican transformaciones lineales a la variable.

1. ESTADÍSTICA
Clase 7
Wendy Plata Alarcón
wplata@espol.edu.ec

2. ESTADÍSTICA
III. MÉTODOS ESTOCÁSTICOS
DISCRETOS
Guayaquil, junio de 2015
Wendy Plata Alarcón
wplata@espol.edu.ec

3. Guayaquil, junio de 2015
Variables Aleatorias Discretas
Estadística para Ingenierías3
 Variable Aleatoria: es una función X cuyo dominio es  y
cuyo conjunto de llegada es R.
 En definitiva su representación como función es X:   R;
lo cual significa que a cada w, la función X le asigna
uno y solo un número real X(w).
 Soporte S de una Variable Aleatoria: conjunto de valores
reales X(w) que ocurren con probabilidad distinta de cero.
 Variable Aleatoria Discreta: X es discreta si su soporte S
es un conjunto contable.

4. Guayaquil, junio de 2015
Variables Aleatorias Discretas:
ejemplo
Estadística para Ingenierías4
 Si un experimento consiste en lanzar tres veces una
moneda “legal” de manera sucesiva siendo cada
lanzamiento independiente del otro; y, se observa que
terna de “lados” ocurre.
 = {sss; ssc; scs; css; scc; csc; ccs; ccc}
 = {w1 ; w2 ; w3 ; w4 ; w5 ; w6 ; w7 ; w8 }
 Dado este experimento, definimos una Variable
Aleatoria X tal que para cualquier w, X(w) es igual
al número de “sellos” en w. Esto hace que:

5. Guayaquil, junio de 2015
Variables Aleatorias Discretas:
ejemplo
Estadística para Ingenierías5
 X(w1) = X(sss) = 3
 X(w2) = X(ssc) = 2
 X(w3) = X(scs) = 2
 X(w4) = X(css) = 2
 X(w5) = X(scc) = 1
 X(w6) = X(csc) = 1
 X(w7) = X(ccs) = 1
 X(w8) = X(ccc) = 0
 Si aplicamos los principios
de probabilidades del
Capítulo previo, tenemos
que para esta Variable
Aleatoria:
8
1
})sss({P)3X(P
8
3
})css{}scs{}ssc({P)2X(P
8
3
})ccs{{csc}}scc({P)1X(P
8
1
})ccc({P)0X(P




Soporte S de la
Variable Aleatoria
Discreta X

6. Guayaquil, junio de 2015
Función de Distribución de
Probabilidades
Estadística para Ingenierías6
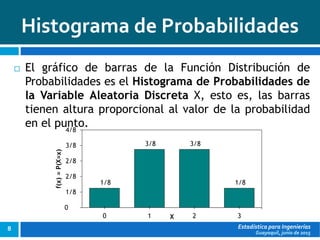
 Con cada Variables Aleatoria Discreta asociaremos una
función f: R  [0,1] a la que llamaremos Función de
Distribución de Probabilidades de X, función que
debe cumplir las siguientes condiciones:
i. f(x) = P(X = x);
ii. .
iii. .
  

Sx Sx
,y;1)xX(P)x(f
  

Sx Ax
)x(f)Ax(P









2,1x;
8
3
3,0x;
8
1
)xX(P)x(f
Ejemplo
X: número de “sellos” en w

7. Guayaquil, junio de 2015
Función de Distribución de
Probabilidades: ejemplo
Estadística para Ingenierías7
 Consideremos la variable aleatoria X cuya Distribución de
Probabilidades es,
f(x) = k(x + 1)2 ; para xS = {0; 1; 2; 3}
 Determinar el valor de k para que f(x) sea una función de Distribución
de probabilidades
 f(x) = (x + 1)2 /30; para xS = {0; 1; 2; 3}
30
1
k1k30
1k16k9k4k
1)13(k)12(k)11(k)10(k
1)3x(P)2x(P)1x(P)0x(P)xX(P
1)xX(P)x(f
2222
3
0x
Sx Sx






 

 

8. Guayaquil, junio de 2015
Histograma de Probabilidades
Estadística para Ingenierías8
 El gráfico de barras de la Función Distribución de
Probabilidades es el Histograma de Probabilidades de
la Variable Aleatoria Discreta X, esto es, las barras
tienen altura proporcional al valor de la probabilidad
en el punto.
1/8
3/8 3/8
1/8
0
1/8
2/8
2/8
3/8
4/8
0 1 2 3
f(x)=P(X=x)
X

9. Guayaquil, junio de 2015
Distribución Acumulada de X
Estadística para Ingenierías9
 Una función de variable real F: R  [0,1] es definida como
la Distribución Acumulada de una Variable Aleatoria
Discreta X si y sólo si:
F(x) = P(X  x), x, esté o no en el Soporte S de X


















3x;1
3x2;
8
7
2x1;
8
4
1x0;
8
1
0x;0
)xX(P)x(F
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,00
-1 0 1 2 3 4
F(X)
X

10. Guayaquil, junio de 2015
Valores Esperados de unVariable
Aleatoria
Estadística para Ingenierías10
 A partir de ahora, pretendemos encontrar los valores
promedios o Valores Esperados de una Variable
Aleatoria Y; cuyo valor y = u(x) está definido en
términos de una Variable Aleatoria X, cuyo soporte es
S y cuya Distribución de Probabilidades es f.
 Se denota por


Sx
)x(u )x(f)x(u)]x(u[E

11. Guayaquil, junio de 2015
Valores Esperados de unVariable
Aleatoria: teorema
Estadística para Ingenierías11
 Si X es una Variable Aleatoria Discreta, ui(x) y i i = 0, 1, 2,
…, n; funciones en X y constantes reales conocidas
respectivamente, entonces:
 Nótese que el Valor Esperado E es una transformación lineal,
puesto que:
 Además, el Valor Esperado de una constante real es la misma
constante: E() = 
 










n
1i
ii
n
1i
ii )]x(u[E)x(uE
)]x(u[E)]x(u[E)]x(u)x(u[E 22112211 

12. Guayaquil, junio de 2015
Valores Esperados de unVariable
Aleatoria: Media
Estadística para Ingenierías12
 Existen funciones de X cuyos Valores Esperados son de
particular utilidad en Estadística, por decir u(x) = xr,
donde r es un entero positivo conocido, el Valor
Esperado de ésta función es también llamado el r-ésimo
Momento de X con respecto al origen; usualmente se lo
denota por ’r esto es:
 Cuando r = 1 se tiene E(x) = ’1 =  valor este, al que se
denomina Media  de la Variable Aleatoria X o también
llamada Esperanza Matemática de X.


Sx
rr'
r )x(fx)x(E

13. Guayaquil, junio de 2015
Valores Esperados de unVariable
Aleatoria: Media
Estadística para Ingenierías13
 Consideremos la variable aleatoria X cuya Distribución
de Probabilidades es,
f(x) = (x + 1)2/30; para xS = {0; 1; 2; 3}
 Determinar la Media  de X usando Valores Esperados.
33.2
3
7
30
70
30
48
30
18
30
4
0
30
)13(
3
30
)12(
2
30
)11(
1
30
)10(
0
30
)1x(
x)x(xf)X(E
2222
3
0x
23
0x








 








 








 








 


  

14. Guayaquil, junio de 2015
Valores Esperados de unVariable
Aleatoria:Varianza
Estadística para Ingenierías14
 Otra función cuyo Valor Esperado es relevante para una
Variable Aleatoria Discreta es (X - )r, que es el r-ésimo
Momento de X con Respecto a su Media , así:
 Cuando r = 2,
 Este Valor Esperado tiene el nombre de Varianza de una
Variable Aleatoria X y se lo denota por 2.


Sx
rr
r )x(f)X()X(E
2'
2
22
2
222
2
)X(E
)X2X(E)X(E



15. Guayaquil, junio de 2015
Valores Esperados de unVariable
Aleatoria:Varianza
Estadística para Ingenierías15
 Consideremos la variable aleatoria X cuya Distribución de
Probabilidades es,
f(x) = (x + 1)2/30; para xS = {0; 1; 2; 3}
 Determinar la Varianza 2 de X usando Valores Esperados.
70.043.513.6
13.6
30
184
30
144
30
36
30
4
0)X(E
30
)13(
3
30
)12(
2
30
)11(
1
30
)10(
0)X(E
30
)1x(
x)x(fx)X(E
)X(E
2
2
2
2
2
2
2
2
2
22
3
0x
2
2
3
0x
22
222









 








 








 








 




 

16. Guayaquil, junio de 2015
Valores Esperados de unVariable
Aleatoria: teorema
Estadística para Ingenierías16
 Sea X una Variable Aleatoria Discreta con Media  y
Varianza 2 y sea Y = X +  entonces:
 Media Y de Y es igual a  + 
 Varianza es 2 2
 Se supone que  y  son constantes reales.
 Prueba
 Y = X +   E(Y) = E(X + )
 E(Y) = E(X) + E()
 E(Y) =  + 

17. Guayaquil, junio de 2015
Valores Esperados de unVariable
Aleatoria: Sesgo
Estadística para Ingenierías17
 El tercer momento de X con respecto a , esto es,
3 = E(X - )3, es utilizado para medir el sesgo o
asimetría de X con respecto a .
 Simetría
 Se puede probar que si el valor de 3 es cero, la
distribución f de X es simétrica con respecto a .
 Asimetría de las Distribuciones
 Si 3 es positivo la distribución es sesgada hacia la
izquierda de ; y, si es negativo el sesgada hacia la
derecha de .

18. Guayaquil, junio de 2015
0,00
0,20
0,40
0,60
0,80
0 1 2 3
f(x)
0,00
0,10
0,20
0,30
0,40
0,50
0 1 2 3
f(x)
0,00
0,20
0,40
0,60
0,80
0 1 2 3
f(x)
Valores Esperados de unVariable
Aleatoria: Sesgo
Estadística para Ingenierías18
a) Sesgo positivo b) Distribución Simétrica
c) Sesgo negativo
3 > 0
3 = 0
3 < 0

19. Guayaquil, junio de 2015
Valores Esperados de unVariable
Aleatoria: Kurtosis
Estadística para Ingenierías19
El cuarto momento de X con respecto a , esto es,
4 = E(X - )4, es llamado Medida de Kurtosis o Medida de
Apuntamiento; lo usual es utilizar el Coeficiente 4 = 4/4
al que se denomina Coeficiente de Apuntamiento de X.
 X es Leptocúrtica
Cuando el Coeficiente de Apuntamiento 4 es mayor a tres.
 X es Platicúrtica
Cuando el Coeficiente de Apuntamiento de X es menor a tres.
 X es Mesocúrtica
Cuando el Coeficiente de Apuntamiento de X es igual a tres.

20. Guayaquil, junio de 2015
Valores Esperados de unVariable
Aleatoria: Kurtosis
Estadística para Ingenierías20
 Medidas de Forma de X
Leptocúrtica
Mesocúrtica
Platicúrtica

21. Guayaquil, junio de 2015
Función Generadora de Momentos
Estadística para Ingenierías21
 Uno de los Valores Esperados más útiles de una Variable
Aleatoria Discreta es la denominada Función Generada de
Momentos, se denota y define de la siguiente manera:
 No es verdad que para todas las Variables Aleatorias existe este
Valor Esperado.
 Si dos Variables X e Y tienen idéntica función Generadora de
Momentos, como consecuencia ambas tienen idéntica
Distribución de Probabilidades, o X e Y son idénticamente
distribuidas.
)a,a(t;)x(fe)e(E)t(M
Sx
xtxt
x  

22. Guayaquil, junio de 2015
Función Generadora de Momentos:
ejemplo
Estadística para Ingenierías22
 Consideremos la variable aleatoria X cuya Distribución de
Probabilidades es,
f(x) = (x + 1)2/30; para xS = {0; 1; 2; 3}
 Determinar la Función Generadora de Momentos.
Rt;e
30
16
e
30
9
e
30
4
30
1
)t(M
30
)13(
e
30
)12(
e
30
)11(
e
30
)10(
e)t(M
30
)1x(
e)x(fe)e(E)t(M
t3t2t
x
2
t3
2
t2
2
t1
2
t0
x
3
0x
2
xt
Sx
xtxt
x








 








 








 








 


  

23. Guayaquil, junio de 2015
Función Generadora de Momentos
Estadística para Ingenierías23
 Si se deriva la Función Generadora de Momentos con
respecto a t y se la evalúa en t = 0, encontramos que:
 La Varianza también puede ser expresada en término
de la Función Generadora de Momentos, de la
siguiente manera:
0t
'
x )t(M)x(E 
2'
x
''
x
22
)]0(M[)0(M)X(E 

24. Guayaquil, junio de 2015
Función Generadora de Momentos:
ejemplo
Estadística para Ingenierías24
 Consideremos la variable aleatoria X cuya Distribución de
Probabilidades es,
f(x) = (x + 1)2/30; para xS = {0; 1; 2; 3}
 A partir de la Función Generadora de Momentos, calcular la
Media y Varianza de X.
 Media
Rt;e
30
16
e
30
9
e
30
4
30
1
)t(M t3t2t
x 
33.2
30
70
30
16
.3
30
9
.2
30
4
e
30
16
.3e
30
9
.2e
30
4
)0(M
0t
t3t2t'
x










25. Guayaquil, junio de 2015
Función Generadora de Momentos:
ejemplo
Estadística para Ingenierías25
 A partir de la Función Generadora de Momentos, calcular la
Media y Varianza de X.
 Varianza
Rt;e
30
16
e
30
9
e
30
4
30
1
)t(M t3t2t
x 
70.043.513.643.5
30
16
.9
30
9
.4
30
4
)33.2(e
30
16
.9e
30
9
.4e
30
4
)]0(M[)0(M
2
2
0t
t3t2t2'
x
''
x
2
















26. Guayaquil, junio de 2015
Distribución Uniforme Discreta
Estadística para Ingenierías26
 Variable Aleatoria Uniforme Discreta con parámetro N
tiene como Distribución de Probabilidades f a la función
siguiente:
 Se suele denotar X  U(1,N), X es una Variable Aleatoria
Uniforme Discreta con Parámetro N.
 Media:  = (N + 1)/2
 Varianza: 2 = (N2 – 1)/12
}N...;;3;2;1{S;
N
1
)x(f)xX(P 

27. Guayaquil, junio de 2015
Experimento Binomial
Estadística para Ingenierías27
 Un Experimento es Binomial cuando y solo cuando lo
constituyen n repeticiones Bernoulli que cumplen las
siguientes condiciones:
 La probabilidad de que una repetición cualquiera ocurra
suceso es p y falla (1 – p);
 La probabilidad de suceso se mantiene invariable durante
todo el experimento;
 Cada una de las repeticiones es independiente de las demás;
y,
 El número n de repeticiones es establecido antes de que el
experimento tenga lugar.

28. Guayaquil, junio de 2015
Distribución Binomial
Estadística para Ingenierías28
 Una Variable Aleatoria Binomial se la representa como
b(x; n, p) y se dice “tenemos una Variable Binomial con
parámetros n y p”.
 Si X es Binomial con parámetros n y p, entonces su
Distribución de Probabilidades es:
 Media:  = np
 Varianza: 2 = np(1 – p)
 Función Generadora de Momentos: Mx(t) = [etp + (1 – p)]n
}n...,,2,1,0{S;Sxtodopara;)p1(p
x
n
)x(f)xX(P xnx






 

29. Guayaquil, junio de 2015
Distribución Binomial
Estadística para Ingenierías29
 Demostración: Media.
 Demostración: Varianza.
np
)p()p1p(n
)pe()]p1(pe[n)0(M
1n
0t
t1nt'
x






 
)p1(np
)np(np)np(np)np(p)1n(nnp
)np(])p()p1p)(1n(n)p()p1p(n[
)np()pe()]p1(pe)[1n(n)pe()]p1(pe[n
)0(M)0(M
2
222222
222n1n2
2
0t
2t2ntt1nt2
2'
x
''
x
2







 





30. Guayaquil, junio de 2015
Distribución Binomial: ejemplo
Estadística para Ingenierías30
 De los correos electrónicos que un profesor encuentra en
su revisión diaria, él ha establecido que el 30% provienen
de estudiantes y el resto de otras fuentes. Una mañana
cualquiera encuentra 35 “e-mails” en su buzón. (Suponga
independencia de los envíos de correos)
 ¿Cuál es la probabilidad que diez de ellos provengan
de sus estudiantes?
 ¿Qué a lo mucho diez de ellos provengan de sus
estudiantes?
 ¿Cuál es el número promedio de correos de
estudiantes que recibe el profesor?

31. Guayaquil, junio de 2015
Distribución Binomial: ejemplo
Estadística para Ingenierías31
 Datos
 Si X es número de correos que recibe el profesor provenientes
de los estudiantes.
 Si denominamos suceso al hecho de que el profesor reciba un
correo proveniente de un estudiante, entonces p = 0.30.
 Si n = 35 correos en el buzón del profesor.
 Se pide:
 ¿Cuál es la probabilidad que diez de ellos provengan de sus
estudiantes?
. 145.0)30.01(30.0
10
35
)10X(P 103510






 

32. Guayaquil, junio de 2015
Distribución Binomial: ejemplo
Estadística para Ingenierías32
 Se pide:
 ¿Qué a lo mucho tres de ellos provengan de sus
estudiantes?
 ¿Cuál es el número promedio de correos de
estudiantes que recibe el profesor?
 = np = 35 (0.30) = 10.50 correos
51.0)10X(P
)30.01(30.0
10
35
...)30.01(30.0
0
35
)10X(P
)10X(P...)2X(P)1X(P)0X(P)10X(P
1035100350

















33. Guayaquil, junio de 2015
Distribución Binomial Negativa
Estadística para Ingenierías33
 Se tiene una sucesión independiente de repeticiones
Bernoulli todas ellas con probabilidad de suceso p; si r
es un número entero previamente determinado,
diremos que X es una Variable Aleatoria Binomial
Negativa si y solo si X representa el número de
repeticiones requeridas para que el r-ésimo suceso
ocurra.

34. Guayaquil, junio de 2015
Distribución Binomial Negativa
Estadística para Ingenierías34
 Si X es Binomial Negativa con parámetros r y p, entonces
su Distribución de Probabilidades es:
 Media:
 Varianza:
 Función Generadora de Momentos:
...},1r,r{S;Sxtodopara;)p1(p
1r
1x
)x(f)xX(P rxr








 
p
r

2
2
p
)p1(r 

1e)p1(para,]e)p1(1[)pe()t(M trtrt
x  

35. Guayaquil, junio de 2015
Distribución Binomial Negativa:
ejemplo
Estadística para Ingenierías35
 Se conoce a través de la experiencia del Departamento
de Calidad de una empresa, que en uno de sus procesos
productivos, el porcentaje de disconformidad es de 15%.
Preocupados por tan alto porcentaje, se procede a la
inspección uno a uno de los productos que se elaboran
en un día:
 ¿Cuál es la probabilidad que el sexto producto
revisado sea el tercero en el que se encuentre una
disconformidad?
 ¿Cuál es la probabilidad que en la cuarta inspección se
encuentre la primera inconformidad?

36. Guayaquil, junio de 2015
Distribución Binomial Negativa:
ejemplo
Estadística para Ingenierías36
 Datos:
 X es el número de repeticiones hasta encontrar la
tercera disconformidad (r = 3).
 La probabilidad de que se encuentra una disconformidad
es p = 0.15.
 Se pide:
 ¿Cuál es la probabilidad que el sexto producto
revisado sea el tercero en el que se encuentre una
disconformidad?
021.0)15.01(15.0
13
16
)6X(P 363








 

37. Guayaquil, junio de 2015
Distribución Binomial Negativa:
ejemplo
Estadística para Ingenierías37
 Datos:
 X es el número de repeticiones hasta encontrar la
primera disconformidad (r = 1).
 La probabilidad de que se encuentra una disconformidad
es p = 0.15.
 Se pide:
 ¿Cuál es la probabilidad que en la cuarta inspección se
encuentre la primera inconformidad?
092.0)15.01(15.0
11
14
)4X(P 141








 

38. Guayaquil, junio de 2015
Distribución Geométrica
Estadística para Ingenierías38
 Supongamos que se tiene una sucesión de repeticiones
Bernoulli, cada una de ellas Independientes de las otras, con
probabilidad de suceso “p”. Diremos que X es una Variable
Aleatoria Geométrica, cuando y sólo cuando, los valores que
ella toma son iguales al número de repeticiones que se
requieren en el experimento, para que el primer suceso
ocurra.
P(X = x) = f(x) = (1 – p)x – 1p; para todo xS
 Media:
 Varianza:
p
1

2
2
p
p1


39. Guayaquil, junio de 2015
Distribución Geométrica: ejemplo
Estadística para Ingenierías39
 Un predicador visita hogares en su afán de difundir la
cristiandad, pero no siempre es bien recibido y escuchado;
sus estimaciones son que en el 15% de los hogares que
visita es bien recibido y escuchado. ¿Cuál es la
probabilidad de que en la quinta visita que haga, sea la
primera vez que el predicador es bien “recibido y
escuchado”?
 Datos:
 Sea X: número de hogares a visitar hasta ser bien “recibido
y escuchado”.
 p = 0.15

40. Guayaquil, junio de 2015
Distribución Geométrica: ejemplo
Estadística para Ingenierías40
 Se pide:
 ¿Cuál es la probabilidad de que en la quinta visita que
haga, sea la primera vez que el predicador es bien
“recibido y escuchado”?
 P(X = 5) = (1 – p)x – 1p = (1 – 0.15)5 – 1(0.15)
 P(X = 5) = (0.85)4(0.15)
 P(X = 5) = 0.0783
 Por lo tanto, la probabilidad de que la quinta visita sea la
primera en la cual el predicador es bien recibido es
0.0783.

41. Guayaquil, junio de 2015
Distribución Poisson
Estadística para Ingenierías41
 En ciencias e ingenierías es común enfrentar problemas en los que
es de interés conocer cómo un determinado hecho ocurre, cada
unidad de tiempo o cada unidad de espacio.
 Una Variable Aleatoria discreta es Poisson con parámetro  cuando
y solo cuando su distribución de probabilidades está dada de la
siguiente manera:
 Media:  = 
 Varianza: 2 = 
 Función Generadora de Momentos:
...},3,2,1,0{S,Sxtodopara;
!x
e
)xX(P
x




Rt,e)t(M )1e(
x
t
 

42. Guayaquil, junio de 2015
Distribución Poisson: ejemplo
Estadística para Ingenierías42
 Los usuarios de un sistema computacional se quejan
de este, ya que el número de veces a la semana que
el mismo falla es considerado muy alto. Al estudiarlo
un grupo de consultores han modelado al número de
“caídas” semanales como una Variable Aleatoria
Poisson con parámetro = 3.2 caídas por semana.
 Determinar la probabilidad de que el sistema falle
cuatro veces una semana cualquiera.
 ¿Cuántas fallas semanales se esperaría que ocurran?

43. Guayaquil, junio de 2015
Distribución Poisson: ejemplo
Estadística para Ingenierías43
 Datos:
 Sea X: número de “caídas” semanales del sistema.
  = 3.2.
 Se pide:
 Determinar la probabilidad de que el sistema falle
cuatro veces una semana cualquiera.
 ¿Cuántas fallas semanales se esperaría que ocurran?
E[X] =  =  = 3.2.
178.0
!4
e2.3
)4X(P
2.34



44. Guayaquil, junio de 2015
Distribución Hipergeométrica
Estadística para Ingenierías44
 Trabajamos con una Población Objetivo constituida
por N entes; entre estos N entes, a tienen una
característica que es de interés en la investigación. Se
toma una Muestra de tamaño n de la Población. Bajo
estas condiciones, X es una Variable Aleatoria
Hipergeométrica con parámetros N, a, n si X
representa el número de elementos que aparecen en
la Muestra, que poseen la característica de interés.

45. Guayaquil, junio de 2015
Distribución Hipergeométrica
Estadística para Ingenierías45
 Si X es Hipergeométrica con parámetros N, a y n,
entonces su Distribución de Probabilidades es:
 Media:
 Varianza:
}n;amin{k};k...,,1,0{S;Sxtodopara;
n
N
xn
aN
x
a
)x(f)xX(P 





















N
an

)1N(N
)nN)(aN(an
2
2




46. Guayaquil, junio de 2015
Distribución Hipergeométrica:
ejemplo
Estadística para Ingenierías46
 En un experimento sobre regresión genética un
biólogo observa un grupo de 25 parejas, 8 de las
cuales tienen el mismo color de ojos y las restantes 17
distintos colores. Se selecciona aleatoriamente una
muestra de 10 parejas.
 ¿Cuál es la probabilidad que ninguna pareja tenga le
mismo color de ojos?
 ¿Qué al menos dos tengan el mismo color de ojos?

47. Guayaquil, junio de 2015
Distribución Hipergeométrica:
ejemplo
Estadística para Ingenierías47
 Datos:
 Población Objetivo: parejas que van a participar en el
experimento, N = 25.
 Característica de interés: que las parejas tengan el
mismo color de ojos, a = 8.
 Tamaño de la Muestra, n = 10.
}8...,,1,0{S;Sxtodopara
;
10
25
x10
825
x
8
)xX(P






















N = 25
n = 10
a = 8

48. Guayaquil, junio de 2015
Distribución Hipergeométrica:
ejemplo
Estadística para Ingenierías48
 ¿Cuál es la probabilidad que ninguna pareja tenga le
mismo color de ojos?
 ¿Qué al menos dos tengan el mismo color de ojos?
006.0
10
25
010
825
0
8
)0X(P 





















935.0
10
25
110
825
1
8
10
25
010
825
0
8
1)2X(P
)]1X(P)0X(P[1)2X(P1)2X(P



























































49. Guayaquil, junio de 2015
Referencias
Estadística para Ingenierías49
 Zurita, G. (2010), “Probabilidad y Estadística:
Fundamentos y Aplicaciones”, Segunda Edición,
Escuela Superior Politécnica del Litoral, Instituto de
Ciencias Matemáticas, Guayaquil-Ecuador.