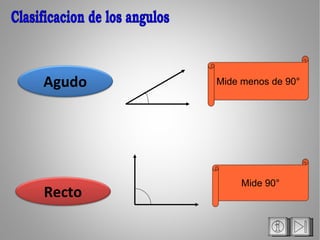
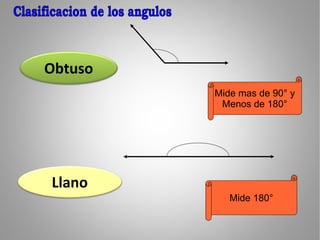
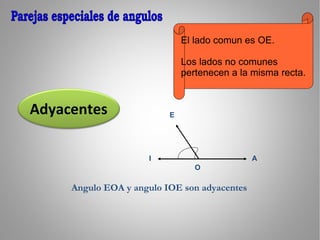
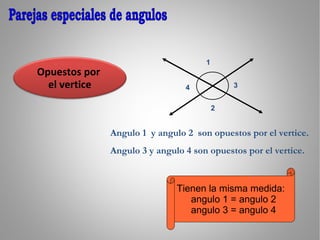
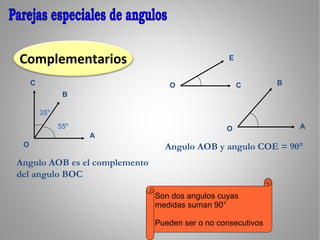
El documento clasifica los ángulos en agudos (menos de 90°), rectos (90°), obtusos (más de 90° pero menos de 180°), llano (180°), y entrantes (más de 180° pero menos de 360°). También describe parejas especiales de ángulos: adyacentes, opuestos por el vértice, complementarios, y suplementarios. Finalmente, presenta tres teoremas sobre ángulos.

1. CLASIFICACIÓN DE ÁNGULOS

2. Mide menos de 90 ° Mide 90 ° Clasificacion de los angulos Recto Agudo

3. Mide mas de 90 ° y Menos de 180° Mide 180° Clasificacion de los angulos Obtuso Llano

4. Mide mas de 180° y menos de 360° Es el giro completo de una linea alrededor del punto donde comienza; esto es, gira hasta ubicarse en su posicion original Clasificacion de los angulos Entrante Perigonal

5. Parejas especiales de angulos Tienen un lado comun, situado entre los lados no comunes. El vertice comun es O O B C A Consecutivos

6. O A E I El lado comun es OE. Los lados no comunes pertenecen a la misma recta. Angulo EOA y angulo IOE son adyacentes Parejas especiales de angulos Adyacentes

7. 1 2 3 4 Angulo 1 y angulo 2 son opuestos por el vertice. Angulo 3 y angulo 4 son opuestos por el vertice. Tienen la misma medida: angulo 1 = angulo 2 angulo 3 = angulo 4 Parejas especiales de angulos Opuestos por el vertice

8. E C O B A O Angulo AOB y angulo COE = 90° Son dos angulos cuyas medidas suman 90 ° Pueden ser o no consecutivos B A C O Angulo AOB es el complemento del angulo BOC 55 ° 35 ° Parejas especiales de angulos Complementarios

9. D O F A B C Angulo ABC + angulo DOF = 180° Son dos angulos cuyas medidas suman 180 ° Pueden ser o no adyacentes 27 ° 153 ° Parejas especiales de angulos Suplementarios