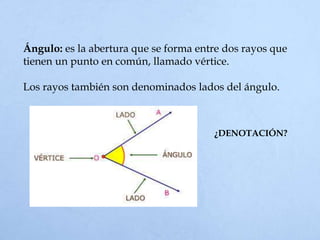
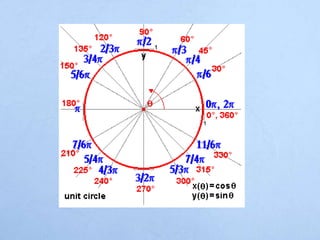
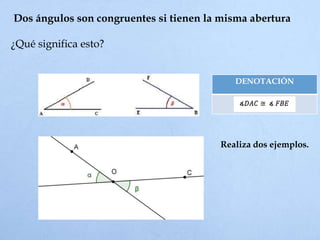
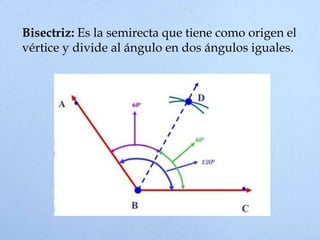
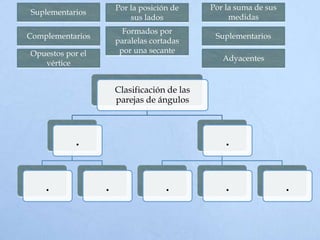
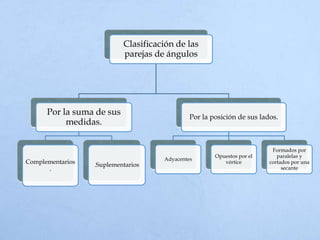
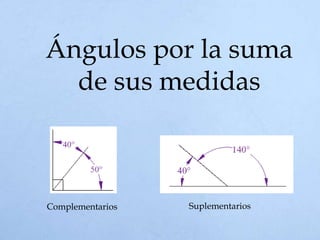
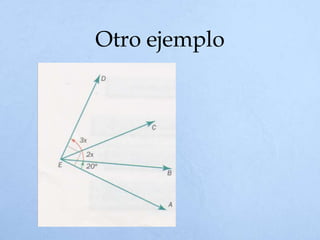
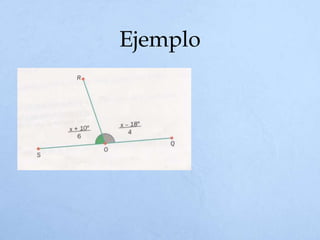
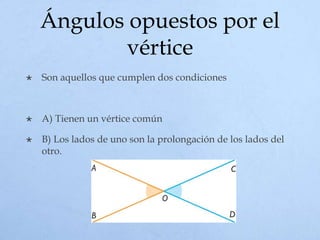
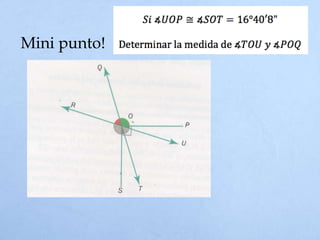
El documento define un ángulo como la abertura formada entre dos rayos que comparten un punto llamado vértice. Explica cómo medir ángulos en grados sexagesimales y radianes, y clasifica los tipos de ángulos como complementarios, suplementarios, adyacentes u opuestos por el vértice dependiendo de la suma de sus medidas o la posición de sus lados.

2. Ángulo: es la abertura que se forma entre dos rayos que
tienen un punto en común, llamado vértice.
Los rayos también son denominados lados del ángulo.
¿DENOTACIÓN?

3. Medición de un ángulo

4. Ejercicios
 Realiza en tu libreta los siguientes ángulos:
 Ángulo de 45º
 Ángulo de 60º
 Ángulo de 100º
 Ángulo de 180º
 Ángulo de 220º
 Ángulo de 315º

5. Sistema sexagesimal y sistema circular
(grados) (radianes)
Ejemplo:
• Expresar en radianes un ángulo de 90º
• Expresar en grados sexagesimales un
ángulo de 6.28 radianes

6.  Ejercicios:
Expresa los siguientes ángulos en el sistema sexagesimal:
 3.14 radianes
 9.42 radianes
 2 radianes
Expresa los siguientes ángulos en el sistema circular:
45º
135º
225º

8. Dos ángulos son congruentes si tienen la misma abertura
¿Qué significa esto?
DENOTACIÓN
Realiza dos ejemplos.

9. Bisectriz: Es la semirecta que tiene como origen el
vértice y divide al ángulo en dos ángulos iguales.

10. Clasificación de las
parejas de ángulos
.
. .
.
. . .
Por la suma de sus
medidas
Por la posición de
sus lados
Complementarios
Opuestos por el
vértice
Suplementarios
Suplementarios
Formados por
paralelas cortadas
por una secante
Adyacentes

11. Clasificación de las
parejas de ángulos
Por la suma de sus
medidas.
Complementarios
.
.Suplementarios
Por la posición de sus lados.
Adyacentes
Opuestos por el
vértice
Formados por
paralelas y
cortados por una
secante

12. Parejas de ángulos
 Ángulos adyacentes: Ángulos con un vértice común y
comparten uno de sus lados
 Ángulo recto: aquel que mide 90º. Se forma cuando se
cortan cuatro ángulos adyacentes congruentes
 Ángulo llano: Es aquel que mide dos ángulos rectos. 180º

13. Ángulos por la suma
de sus medidas
Complementarios Suplementarios

14. Ángulos complementarios
 Son los ángulos cuyas medidas suman un ángulo recto. Un
ángulo es complementario de otro si son adyacentes y
suman 90º
= 55º
B
AC
D

15. Otro ejemplo

16. Ángulos suplementarios
 Son ángulos adyacentes cuyas medidas suman exactamente
180°
D
EF
G
¿Cómo escribirías una ecuación con la
denotación correspondiente?

17. Ejemplo

18. ¿Qué pasa cuando nos
quedan grados con decimal?

19. Ejemplo
 Determina el suplemento de 54° 12’
 Determina el complemento de 25° 35’ 14”

20. También puedes utilizar la
calculadora!

21. Ángulos por la
posición de sus lados
Adyacentes
Opuestos por el vértice
Formados por paralelas y
cortados por una secante

22. Ángulos opuestos por el
vértice
 Son aquellos que cumplen dos condiciones
 A) Tienen un vértice común
 B) Los lados de uno son la prolongación de los lados del
otro.

23. Ejemplo!

24. Mini punto!