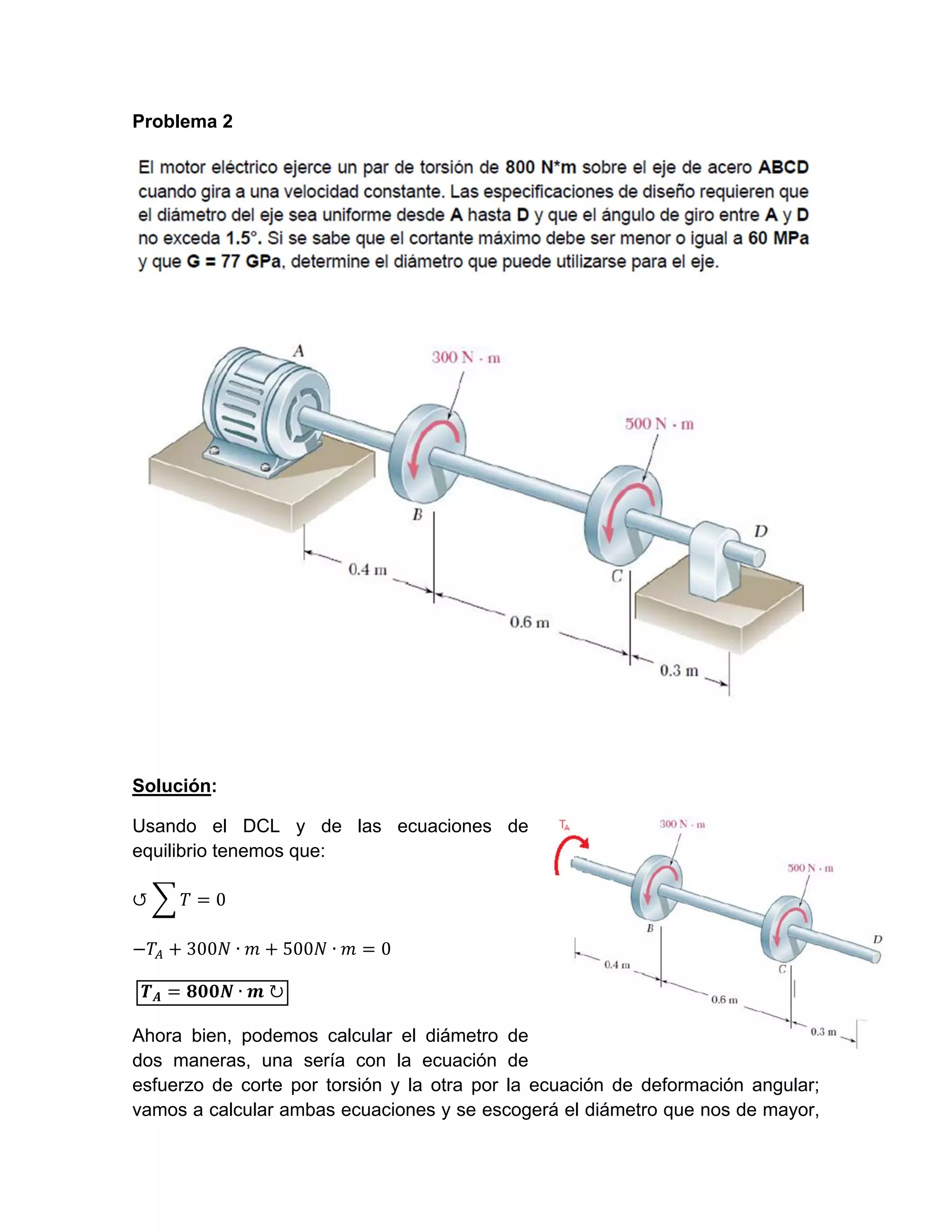
El documento describe el cálculo del diámetro de un eje utilizando dos métodos: esfuerzo de corte por torsión y deformación angular. Se calculan los diámetros obtenidos de ambas ecuaciones y se elige el mayor, que en este caso es 42,07 mm, verificando que no fallará por corte. Finalmente, se concluye que el diámetro elegido es adecuado para el eje sin riesgo de falla.

1. Problema 2
Solución:
Usando el DCL y de las ecuaciones de
equilibrio tenemos que:
↺ 0
300 ∙ 500 ∙ 0
∙ ↻
Ahora bien, podemos calcular el diámetro de
dos maneras, una sería con la ecuación de
esfuerzo de corte por torsión y la otra por la ecuación de deformación angular;
vamos a calcular ambas ecuaciones y se escogerá el diámetro que nos de mayor,

2. luego recalculamos en la otra ecuación para verificar que con éste diámetro
escogido no fallará.
 Calculo por esfuerzo de Corte por torsión:
La ecuación de esfuerzo de corte por torsión se muestra a continuación;
despejando el radio, tenemos que:
2
2
→
2
Reemplazando valores, tenemos que:
2 2 800
60 10 ⁄
8,48826 → 0,0204
El diámetro (dado en mm) se calcula de la siguiente manera:
2 2 0,0204 0.0408
1000
1
40,8
 Calculo por deformación angular:
La ecuación de la deformación angular se muestra a continuación:
∅
Ahora bien, como tenemos que el ángulo de giro esta entre A y D ∅ / 1,5° ,
transformemos el valor del ángulo de giro a radianes así:
∅ / 1,5°
180°
0,02618
Ahora bien,: calcularemos las deformaciones parciales entre los puntos AB, BC y
CD y luego algebraicamente la igualamos y despejamos el diámetro ya allí
sabemos cuál es su valor
∅ / ∅ / ∅ / ∅ /
Donde:
∅ /
800 0,4
77 10 ⁄
32
4,23311 10

3. ∅ /
500 0,6
77 10 ⁄
32
3,96854 10
∅ /
0 0,6
77 10 ⁄
32
0
Reemplazando valores, tenemos que:
∅ / 0,02618
4,23311 10 3,96854 10
0
Despejamos el valor de y nos queda que:
4,23311 3,96854 10
0,02618
3,13279 10 → 0,04207
El diámetro (dado en mm) se calcula de la siguiente manera:
0.04207
1000
1
42,07
Podemos tomar el diámetro mayor para ser el diámetro del eje; pero antes
corroboremos si con éste diámetro no fallará por corte:
2
32
16 16 800
42,07
1000
1
54,72 60 ‼
Como pudimos comprobar que con 42,07 no fallará por cortante, entonces:
,