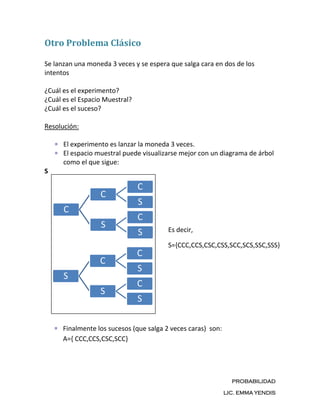
Este documento define conceptos básicos de probabilidad como experimento aleatorio, espacio muestral, suceso, intersección de sucesos, sucesos disjuntos, unión de sucesos y complemento de sucesos. Incluye ejemplos para ilustrar cada concepto y presenta la definición axiomática de probabilidad a través de tres axiomas y cuatro consecuencias.

1. EXPERIMENTO ALEATORIO, ESPACIO
MUESTRAL Y SUCESO
Experimento aleatorio: Es una acción o proceso que puede tener
distintos resultados posibles, y cuyo resultado no se conoce hasta que no se
lleva a cabo.
Ejemplos:
tirar una moneda
tirar un dado
medir la cantidad de milímetros de lluvia caídos
elegir un número al azar
Espacio muestral: El conjunto de todos los posibles resultados de un
experimento aleatorio se llama espacio de la muestra del experimento. La
muestra es el espacio denominado S.
Ejemplos:
Si el experimento consiste en arrojar un dado y observar el número
que sale, el espacio muestral es: S = {1,2,3,4,5,6}
Si el experimento consiste en tomar un libro al azar de la biblioteca y
ver con qué letra empieza el título, el espacio muestral es: S = {A, B, C,
D, E, F, G, H, I, J, K, L, M, N, Ñ, O, P, Q, R, S, T, U, V, W, X, Y, Z}
Si el experimento consiste en tirar una moneda y ver qué sale, el
espacio muestral es: S = {cara, sello}
PROBABILIDAD
LIC. EMMA YENDIS

2. Suceso o Evento: Es un subconjunto del espacio muestral.
Ejemplos:
En el experimento de arrojar un dado y ver qué sale, el espacio
muestral es: S = {1, 2, 3, 4, 5, 6}. Cualquier subconjunto de S es un suceso, por
lo tanto ejemplos de sucesos de este experimento pueden ser:
{1}
{6}
Un evento que no
{3, 4}
puede ocurrir se
{4, 5, 6}
conoce como "suceso
{1, 3, 5}
nulo", "suceso falso" o
{2, 4, 6}
"suceso
imposible". Además
de la notación {} se
puede usar la
alternativa .
PROBABILIDAD
LIC. EMMA YENDIS

3. TEORÍA DE CONJUNTOS
(Operaciones entre eventos: Unión, intersección, complemento, eventos
mutuamente excluyentes, diferencia, diferencia simétrica.)
1) Intersección de sucesos: Dados A y B dos sucesos, A B es el suceso que
ocurre cuando ocurren simultáneamente A y B. Se puede llamar "A
intersección B" o bien "A y B".
S Ejemplo:
Se tira un dado, y se definen
los sucesos:
A: que salga menos de 4
B: que salga más de 2
Con lo cual queda:
A = {1, 2, 3}
B = {3, 4, 5, 6}
A B = {3}
2) Sucesos disjuntos o mutuamente excluyentes: Son los sucesos cuya
intersección es nula. Dados los sucesos A y B, son disjuntos <=> A B = .
S Ejemplo:
Se tira un dado, y se definen
los sucesos:
A: que salga 1 ó 2
B: que salga más de 4
Con lo cual queda:
A = {1, 2}
B = {5, 6}
A B=
Como A y B tienen intersección nula, no pueden suceder simultáneamente.
PROBABILIDAD
LIC. EMMA YENDIS

4. 3) Unión de sucesos: Dados A y B dos sucesos, A B es el suceso que ocurre
cuando ocurre A, B, o los dos simultáneamente. Se puede llamar "A unión
B" o bien "A ó B".
S
Ejemplo:
Se tira un dado, y se definen
los sucesos:
A: que salga menos de 4
B: que salga 2 ó 6
Con lo cual queda:
A = {1, 2, 3}
B = {2, 6}
A B = {1, 2, 3, 6}
4) Complemento de los sucesos: Dado un suceso A, su "complemento" es el
suceso que ocurre si y sólo si NO ocurre A (y A ocurre si y sólo si no ocurre
C
el complemento de A). El complemento de A se escribe A o bien A y se
llama "complemento de A"
S Ejemplo:
Se arroja un dado, y el suceso A es que salga
un 4, entonces el suceso AC es que no salga
un 4 o bien que salga 1, 2, 3, 5 ó 6.
Expresados como conjuntos quedan:
S = {sale 1, sale 2, sale 3, sale 4, sale 5, sale 6}
A = {sale 4}
C
A = {sale 1, sale 2, sale 3, sale 5, sale 6}
PROBABILIDAD
LIC. EMMA YENDIS

5. A AC = S, es decir, la unión de A y AC
forma S. Esto es lógico: O llueve o no
llueve. No hay ninguna otra posibilidad.
A AC = . Un suceso y su
complemento son disjuntos, porque no
pueden ocurrir al mismo tiempo. No
puede "llover" y "no llover" al mismo
tiempo.
Problema típico
Se lanza un dado y se espera obtener un 3.
¿Cuál es el experimento?
¿Cuál es el espacio muestral?
¿Cuál es el suceso?
Resolución:
Lanzar el dado es el experimento
El espacio muestral es S= {1,2,3,4,5,6}
El suceso es que se pueda obtener un 3, es decir A={3}
PROBABILIDAD
LIC. EMMA YENDIS

6. PROBABILIDAD
LIC. EMMA YENDIS

7. Otro Problema Clásico
Se lanzan una moneda 3 veces y se espera que salga cara en dos de los
intentos
¿Cuál es el experimento?
¿Cuál es el Espacio Muestral?
¿Cuál es el suceso?
Resolución:
El experimento es lanzar la moneda 3 veces.
El espacio muestral puede visualizarse mejor con un diagrama de árbol
como el que sigue:
S
C
C
S
C
C
S Es decir,
S
S={CCC,CCS,CSC,CSS,SCC,SCS,SSC,SSS}
C
C
S
S
C
S
S
Finalmente los sucesos (que salga 2 veces caras) son:
A={ CCC,CCS,CSC,SCC}
PROBABILIDAD
LIC. EMMA YENDIS

8. PROBABILIDAD
Introducción
¿Qué es la probabilidad?
La probabilidad expresa el grado de certeza de que ocurrirá un
determinado suceso al hacer un determinado experimento
aleatorio.
Cuanto más alta es la probabilidad de un suceso, mayor es el
grado de certeza de que ocurrirá al hacer el experimento
aleatorio.
Dado un suceso A, escribimos su probabilidad como P(A).
Definición axiomática de probabilidad.
La definición axiomática consta de los siguientes tres axiomas:
Axioma 1: P(A) 0
"La probabilidad no puede ser negativa"
Axioma 2: P(S) = 1
"La probabilidad del espacio muestral es uno"
Axioma 3: A B= <=> P(A B) = P(A) + P(B)
"Dos sucesos son disjuntos si y sólo si la probabilidad de su unión es
la suma de sus probabilidades".
PROBABILIDAD
LIC. EMMA YENDIS

9. De los tres axiomas, se deducen casi inmediatamente cuatro
consecuencias:
Consecuencia 1: P(A) 1
"La probabilidad tampoco puede ser mayor que uno"
Consecuencia 2: P(A) + P(AC) = 1
"Las probabilidades de dos sucesos complementarios suman uno"
Consecuencia 3: P( ) = 0
"La probabilidad de un suceso imposible es cero"
Consecuencia 4: P(A B) = P(A) + P(B) - P(A B)
La probabilidad de la unión de dos sucesos es la suma de sus
probabilidades menos la probabilidad de la intersección.
PROBABILIDAD
LIC. EMMA YENDIS