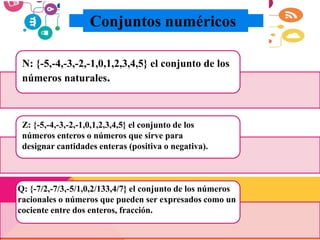
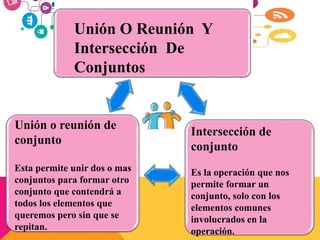
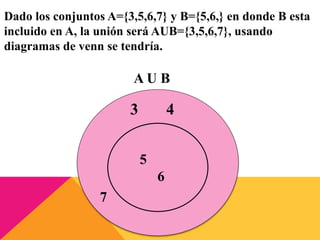
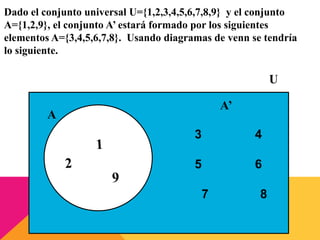
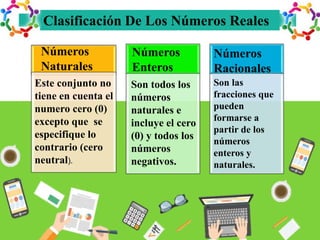
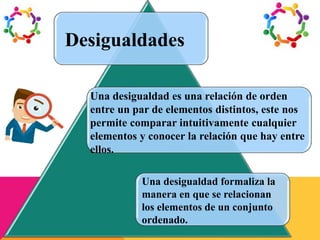
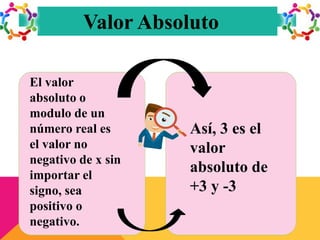
Este documento presenta información sobre conjuntos y números reales. Define qué son los conjuntos y menciona algunos conjuntos numéricos como los naturales, enteros y racionales. Explica operaciones con conjuntos como la unión, intersección y complemento. Finalmente, describe la clasificación y propiedades de los números reales, incluyendo desigualdades y valor absoluto.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN
UNIVERSITARIA
UNIVERSIDAD POLITÉCNICA TERRITORIAL DEL ESTADO
LARA ANDRÉS ELOY BLANCO
PROGRAMA NACIONAL DE FORMACIÓN EN CONTADURÍA
PÚBLICA
Barquisimeto, Febrero 2021
Conjuntos Y Números Reales
Participante:
Infante Audimar
C.I 29.972.913
Sección: 0102

2. Conjuntos
Un conjunto lo forman unos
elementos de su misma
naturaleza es decir,
elementos diferenciados
entre si pero que poseen en
común ciertas propiedades o
características.
Este puede tener entre
ellos, o con los elementos de
otros conjuntos, ciertas
relaciones. Un conjunto
puede tener un número
finito o infinito de
elementos.

3. Conjuntos numéricos
N: {-5,-4,-3,-2,-1,0,1,2,3,4,5} el conjunto de los
números naturales.
Z: {-5,-4,-3,-2,-1,0,1,2,3,4,5} el conjunto de los
números enteros o números que sirve para
designar cantidades enteras (positiva o negativa).
Q: {-7/2,-7/3,-5/1,0,2/133,4/7} el conjunto de los números
racionales o números que pueden ser expresados como un
cociente entre dos enteros, fracción.

4. Subconjuntos De
Un Conjunto
Un conjunto C y una
propiedad P de un
elemento genérico de C,
los elementos de C que
poseen esa propiedad
forman un nuevo
conjunto S llamado
subconjunto de C.
Notaciones Con
Conjunto
Sea un conjunto con
ciertos elementos,
consideramos el conjunto
N de los números
naturales N:{0,1,2,3,4,5}
para expresar que un
determinado elemento
pertenece a N.

5. Operación Con Conjuntos
Las operaciones con
conjunto también
conocidas como algebra
de conjuntos, nos
permiten realizar
operaciones sobre los
conjunto para obtener
otro conjunto.

6. Unión O Reunión Y
Intersección De
Conjuntos
Unión o reunión de
conjunto
Esta permite unir dos o mas
conjuntos para formar otro
conjunto que contendrá a
todos los elementos que
queremos pero sin que se
repitan.
Intersección de
conjunto
Es la operación que nos
permite formar un
conjunto, solo con los
elementos comunes
involucrados en la
operación.

7. Ejercicio de Unión de conjunto
Dado los conjuntos A= {1,2,3,4,5,6,7} y B={8,9,10,11} la unión de
estos conjuntos será A U B={1,2,3,4,5,6,7,8,9,10,11}, usando
diagramas venn se tendría lo siguiente:
A U B
2
1 3

8. Dado los conjuntos A={3,5,6,7} y B={5,6,} en donde B esta
incluido en A, la unión será AUB={3,5,6,7}, usando
diagramas de venn se tendría.
3 4
5
6
7
A U B

9. Complemento De Un Conjunto
Es la operación que
nos permite formar un
conjunto con todos los
elementos del
conjunto de referencia
o universal , que no
están en el conjunto.
En esta operación el
complemento de un
conjunto se denota con
un apostrofe sobre el
conjunto que se opera,
A` en donde el
conjunto A es el
conjunto del cual se
hace la operación de
complemento.

10. Dado el conjunto universal U={1,2,3,4,5,6,7,8,9} y el conjunto
A={1,2,9}, el conjunto A’ estará formado por los siguientes
elementos A={3,4,5,6,7,8}. Usando diagramas de venn se tendría
lo siguiente.
U
A
A’
3 4
5 6
7 8

11. Números Reales
Los números reales son todos
los números que encontramos
mas frecuentemente dado que
los números complejos no se
encuentran de manera
accidental, sino que tienen que
buscarse expresamente.
Los números reales se
representan mediante la letra
R.

12. Clasificación De Los Números Reales
Números
Naturales
Este conjunto no
tiene en cuenta el
numero cero (0)
excepto que se
especifique lo
contrario (cero
neutral).
Números
Enteros
Son todos los
números
naturales e
incluye el cero
(0) y todos los
números
negativos.
Números
Racionales
Son las
fracciones que
pueden
formarse a
partir de los
números
enteros y
naturales.

13. Números
Irracionales
Son números
decimales que no
pueden expresarse
ni de manera
exacta ni de
manera periódica.

14. Desigualdades
Una desigualdad es una relación de orden
entre un par de elementos distintos, este nos
permite comparar intuitivamente cualquier
elementos y conocer la relación que hay entre
ellos.
Una desigualdad formaliza la
manera en que se relacionan
los elementos de un conjunto
ordenado.

15. Valor Absoluto
El valor
absoluto o
modulo de un
número real es
el valor no
negativo de x sin
importar el
signo, sea
positivo o
negativo.
Así, 3 es el
valor
absoluto de
+3 y -3

16. Una desigualdad de
valor absoluto es
una desigualdad
que tiene un signo
de valor absoluto
con una variable
dentro.
Desigualdades De Valor Absoluto

17. Bibliografía
Robert Argand (1806)
José María, Maza Sáez (2008)
Nahin Paul (hardcover, 1998)
Robertson Edmund.