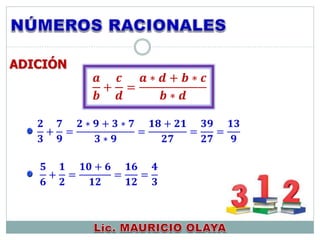
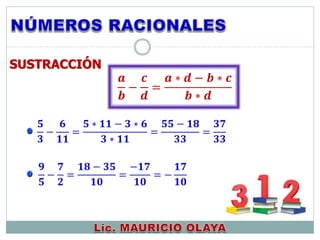
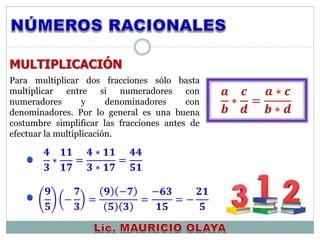
Este documento presenta información sobre números reales. Explica cómo resolver problemas utilizando propiedades de números reales y sus relaciones y operaciones. También cubre temas como representaciones de números reales, términos, valor absoluto, tablas de multiplicar, leyes de signos para suma y multiplicación, y fracciones.

1. NÚMEROS REALES

2. NÚMEROS REALES
Resuelvo problemas y simplifico
cálculos usando propiedades y
relaciones de los números reales y
de las relaciones y operaciones
entre ellos.
Utilizo números reales en sus
diferentes representaciones y en
diversos contextos.
COMPETENCIAS MATEMÁTICAS

4. NÚMEROS REALES
TÉRMINO:
Una combinación de número o letras que
junto a un signo aritmético forman las
expresiones o ecuaciones matemáticas.
Ejemplo:
4
n
x3
xy3
2

1) Término
2) Valor absoluto
3) Tablas de
multiplicar
4) Ley de los
signos para la
suma
5) Ley de los
signos para la
multiplicación

5. NÚMEROS REALES
VALOR ABSOLUTO:
Es la distancia que hay desde el número
indicado hasta el cero, se designa con dos
barras verticales.
Ejemplo: 22 
55 
4
1
4
1

1) Término
2) Valor absoluto
3) Tablas de
multiplicar
4) Ley de los
signos para la
suma
5) Ley de los
signos para la
multiplicación

6. Requisitos
NÚMEROS REALES
Debes saber las tablas de multiplicar de
memoria.
Se recomienda estudiarlas si no las
dominas bien.
En particular se deben conocer los
cuadrados de los números del 1 al 20.
Ejemplos:
(6)(8) = 48
42 = 16
152 = 225
1) Término
2) Valor absoluto
3) Tablas de
multiplicar
4) Ley de los
signos para la
suma
5) Ley de los
signos para la
multiplicación

7. Cuando los números enteros tienen el mismo signo,
se suman y el resultado queda con el mismo signo
de los números sumados.
219462 
16853 

8. Cuando los números enteros tienen distinto signo,
se resta el mayor (en valor absoluto) con el menor
(en valor absoluto) y el resultado (en valor absoluto)
queda con el signo del mayor.
Ejemplo:
235 
426 

9. Si delante de un paréntesis, corchete o llave, no hay
nada o un signo positivo, entonces se considera
que hay un signo positivo que al retirar el paréntesis
mantiene el signo de los términos que estaban dentro
de el.
Ejemplo:
      54235423 
 5423 
5423 
0

10. Si delante de un paréntesis, corchete o llave, hay un
signo negativo, entonces al retirar el paréntesis se
cambia el signo de los términos que estaban dentro
de el.
Ejemplo:
 412 
412 
1
      412412 

11. Para sumar o restar números enteros
Eliminar los paréntesis, llaves y corchetes aplicando
las propiedades que correspondan.
Sumar primero todos los positivos por un lado y los
negativos por otro poniéndoles el signo correspondiente al
resultado de cada uno.
Restar ambos y poner el signo del mayor a la diferencia.

12. Ejemplos
NÚMEROS ENTEROS
1. Resolver:
        853514952757 
      853514952757 
    853514952757 
Ahora elimine los
corchetes.
853514952757 Ahora elimine las
llaves.
Sume los positivos
y luego sume el
valor absoluto de
los negativos
poniendo el
resultado con
signo negativo y
finalmente reste.
4327
16
Elimine primero,
los paréntesis.

13. Ejercicios
NÚMEROS ENTEROS
1. Resolver:
Respuesta: -10
2. Resolver:
Respuesta: 4
3. Resolver:
Respuesta: 4
        53167132513 
     932157434383  )(
      9257610364 

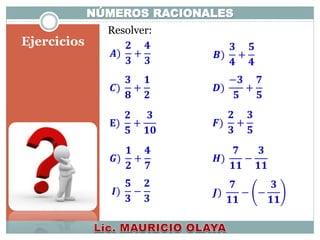
14. Ejercicios
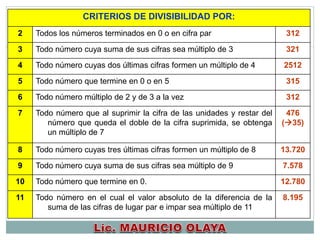
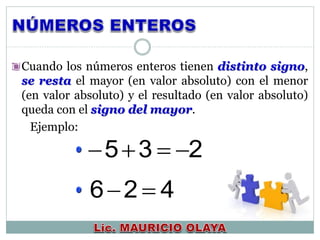
NÚMEROS ENTEROS
4. Resolver:
A) 5 + (-8) + (-9) + 7
B) –8 + (-7) + 3 + 9
C) –6 + 5 + (-2) + (-1)
D) 12 + 7 + (-37) + 14
E) (-23) + (-35) + 43 + (-33)
F) (-63) + 45 + (-38) + 17
G) 3462 + (-5237) + (-1304) + (-7064)
H) 2062 + (-3896) + 6438 + (-7068)
I) [(-2) – 4] – (-7)
J) –2 – [4 – (-7)]
-5
-3
-4
-4
-48
-39
-10143
-2464
1
-13
Respuesta

15. Para hallar el producto de dos números enteros:
Se multiplican sus valores absolutos.
El producto es un número positivo si los dos números tienen
el mismo signo.
El producto es un número negativo si los dos números tienen
el signo diferente.
Regla de los signos de la multiplicación:
15)5)(3( 
42)7)(6( 
(+) (+) = (+)
(+) (-) = (-)
(-) (+) = (-)
(-) (-) = (+)

16. Cociente de dos números enteros:
En una división exacta se cumple siempre:
Dividendo = divisor x cociente
Dividir dos números entre sí es encontrar un tercer número
cuyo producto por el divisor nos de el dividendo.
Regla de los signos de la división:
3)5()15( 
6)7()42( 
(+)÷(+) = (+)
(+) ÷ (-) = (-)
(-) ÷ (+) = (-)
(-) ÷ (-) = (+)

17. Es un conjunto infinito, ordenado y denso, donde todos los
números se pueden escribir como fracción, es decir:
a
b
/ a y b son enteros, y b es distinto de ceroQ =
15,
0 NO es racional
a: numerador y b: denominador
23;19;0;4;3 
13
2
;
9
7
;
5
4
;
2
1

1,1;723,0;35,2;5,0 

18. Fracción propia, donde el numerador es menor que el
denominador.
Fracción impropia, donde el numerador es mayor que el
denominador.
Fracción Mixta, está compuesta de una parte entera y de
otra fraccionaria.
Las fracciones se pueden clasificar en:
𝟒
𝟓
𝟏𝟎
𝟕
𝟐
𝟏
𝟑

19. Simplificar una fracción:
Simplificar una fracción, significa dividir, tanto el numerador
como el denominador por un mismo número.
𝟑𝟔
𝟒𝟓
=
𝟑𝟔 ÷ 𝟗
𝟒𝟓 ÷ 𝟗
=
𝟒
𝟓
𝟐𝟎
𝟔𝟎
=
𝟐𝟎 ÷ 𝟏𝟎
𝟔𝟎 ÷ 𝟏𝟎
=
𝟐 ÷ 𝟐
𝟔 ÷ 𝟐
=
𝟏
𝟑

20. ADICIÓN
Se analiza primero si tienen el mismo denominador, de ser así
se coloca el mismo denominador y se efectúa la suma entre
numeradores. Toda respuesta deberá simplificarse hasta donde
sea posible.
𝟏
𝟑
+
𝟕
𝟑
=
𝟖
𝟑
𝟐
𝟓
+
𝟒
𝟓
+
𝟔
𝟓
+
𝟕
𝟓
=
𝟏𝟗
𝟓

21. ADICIÓN
Si los denominadores son diferentes el procedimiento consiste
en multiplicar los denominadores entre si y poner el resultado
como el nuevo denominador de la expresión resultado. Luego se
multiplican el numerador de la primera expresión con el
denominador de la segunda expresión para sumarlo con la
multiplicación del denominador de la primera expresión con el
numerador de la segunda expresión. Esta multiplicación que
algunas personas llaman “en cruz” o “cruzados”, se pone en el
numerador de la fracción resultado. Toda respuesta deberá
simplificarse hasta donde sea posible.

22. ADICIÓN
𝟐
𝟑
+
𝟕
𝟗
=
𝟐 ∗ 𝟗 + 𝟑 ∗ 𝟕
𝟑 ∗ 𝟗
=
𝟏𝟖 + 𝟐𝟏
𝟐𝟕
=
𝟑𝟗
𝟐𝟕
=
𝟏𝟑
𝟗
𝟓
𝟔
+
𝟏
𝟐
=
𝟏𝟎 + 𝟔
𝟏𝟐
=
𝟏𝟔
𝟏𝟐
=
𝟒
𝟑
𝒂
𝒃
+
𝒄
𝒅
=
𝒂 ∗ 𝒅 + 𝒃 ∗ 𝒄
𝒃 ∗ 𝒅

23. SUSTRACCIÓN
𝟓
𝟑
−
𝟔
𝟏𝟏
=
𝟓 ∗ 𝟏𝟏 − 𝟑 ∗ 𝟔
𝟑 ∗ 𝟏𝟏
=
𝟓𝟓 − 𝟏𝟖
𝟑𝟑
=
𝟑𝟕
𝟑𝟑
𝟗
𝟓
−
𝟕
𝟐
=
𝟏𝟖 − 𝟑𝟓
𝟏𝟎
=
−𝟏𝟕
𝟏𝟎
= −
𝟏𝟕
𝟏𝟎
𝒂
𝒃
−
𝒄
𝒅
=
𝒂 ∗ 𝒅 − 𝒃 ∗ 𝒄
𝒃 ∗ 𝒅

24. MULTIPLICACIÓN
𝟒
𝟑
∗
𝟏𝟏
𝟏𝟕
=
𝟒 ∗ 𝟏𝟏
𝟑 ∗ 𝟏𝟕
=
𝟒𝟒
𝟓𝟏
𝟗
𝟓
−
𝟕
𝟑
=
𝟗 −𝟕
𝟓 𝟑
=
−𝟔𝟑
𝟏𝟓
= −
𝟐𝟏
𝟓
𝒂
𝒃
∗
𝒄
𝒅
=
𝒂 ∗ 𝒄
𝒃 ∗ 𝒅
Para multiplicar dos fracciones sólo basta
multiplicar entre si numeradores con
numeradores y denominadores con
denominadores. Por lo general es una buena
costumbre simplificar las fracciones antes de
efectuar la multiplicación.

25. DIVISIÓN
𝟕
𝟐
÷
𝟑
𝟖
=
𝟕 ∗ 𝟖
𝟐 ∗ 𝟑
=
𝟓𝟔
𝟔
=
𝟐𝟖
𝟑
𝒐𝒕𝒓𝒂 𝒇𝒐𝒓𝒎𝒂
𝟕
𝟐
𝟑
𝟖
=
𝟓𝟔
𝟔
=
𝟐𝟖
𝟑
𝟗
𝟓
÷ −
𝟕
𝟑
=
𝟗 𝟑
𝟓 −𝟕
=
𝟐𝟕
−𝟑𝟓
= −
𝟐𝟕
𝟑𝟓
𝒂
𝒃
÷
𝒄
𝒅
=
𝒂 ∗ 𝒅
𝒃 ∗ 𝒄
Para dividir dos fracciones se toma la primera
fracción (dividendo) y se multiplica por el
inverso multiplicativo de la otra fracción
(divisor). Se simplifica el cociente si se es
posible.

26. POTENCIACIÓN Y RADICACIÓN
𝟑
𝟐
𝟒
=
𝟑 𝟒
𝟐 𝟒
=
𝟖𝟏
𝟏𝟔
−
𝟗
𝟓
𝟑
=
−𝟗 𝟑
𝟓 𝟑
=
−𝟕𝟐𝟗
𝟏𝟐𝟓
= −
𝟕𝟐𝟗
𝟏𝟐𝟓
𝒂
𝒃
𝒏
=
𝒂 𝒏
𝒃 𝒏
𝒏 𝒂
𝒃
=
𝒂
𝒃
𝟏
𝒏
=
𝒏
𝒂
𝒏
𝒃
𝟑 𝟏𝟐𝟓
𝟐𝟕
=
𝟑
𝟏𝟐𝟓
𝟑
𝟐𝟕
=
𝟓
𝟑

27. NÚMEROS RACIONALES
Ejercicios
Resolver:
𝑨)
𝟐
𝟑
+
𝟒
𝟑
𝑩)
𝟑
𝟒
+
𝟓
𝟒
𝑪)
𝟑
𝟖
+
𝟏
𝟐
𝑫)
−𝟑
𝟓
+
𝟕
𝟓
𝐄)
𝟐
𝟓
+
𝟑
𝟏𝟎
𝑭)
𝟐
𝟑
+
𝟑
𝟓
𝑮)
𝟏
𝟐
+
𝟒
𝟕
𝑯)
𝟕
𝟏𝟏
−
𝟑
𝟏𝟏
𝑰)
𝟓
𝟑
−
𝟐
𝟑
𝑱)
𝟕
𝟏𝟏
− −
𝟑
𝟏𝟏

28. NÚMEROS RACIONALES
Ejercicios
Resolver:
𝑲)
𝟏
𝟐
÷
𝟑
𝟖
𝑳)
𝟐
𝟓
÷
𝟑
𝟏𝟎
𝑴)
𝟐
𝟓
∗
𝟑
𝟕
𝑵)
𝟑
𝟖
∗
𝟑
𝟓
𝑶)
𝟒
𝟓
∗
𝟕
𝟑
𝑷)
𝟓
𝟕
∗
𝟐
𝟑
𝐐)
𝟓
𝟐
∗
𝟑
𝟏𝟎
𝑹)
−𝟓
𝟑
∗
𝟐
−𝟕
𝑺)
𝟐
−𝟓
∗
−𝟑
𝟕
𝑻)
𝟑
𝟕
÷
−𝟐
𝟑

29. Cuando hay mezcla de sumas, productos, paréntesis,
etc…
Primero se realizan los PARÉNTESIS, si les hay. Si hay
paréntesis anidados ( uno dentro de otro) se opera de dentro
hacia fuera.
Segundo las POTENCIAS y RAÍCES, si las hay.
Tercero los PRODUCTOS y DIVISIONES, si los hay.
Cuarto las SUMAS y RESTAS, si las hay
Si hay una igualdad en el orden o jerarquía en las operaciones,
se opera de IZQUIERDA a DERECHA.
GERARQUÍA EN LAS OPERACIONES

30. CRITERIOS DE DIVISIBILIDAD POR:
2 Todos los números terminados en 0 o en cifra par 312
3 Todo número cuya suma de sus cifras sea múltiplo de 3 321
4 Todo número cuyas dos últimas cifras formen un múltiplo de 4 2512
5 Todo número que termine en 0 o en 5 315
6 Todo número múltiplo de 2 y de 3 a la vez 312
7 Todo número que al suprimir la cifra de las unidades y restar del
número que queda el doble de la cifra suprimida, se obtenga
un múltiplo de 7
476
(35)
8 Todo número cuyas tres últimas cifras formen un múltiplo de 8 13.720
9 Todo número cuya suma de sus cifras sea múltiplo de 9 7.578
10 Todo número que termine en 0. 12.780
11 Todo número en el cual el valor absoluto de la diferencia de la
suma de las cifras de lugar par e impar sea múltiplo de 11
8.195

31. NÚMEROS REALES