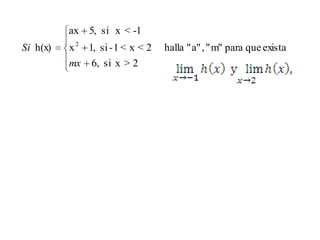Para analizar el límite de una función en un punto, es necesario acercarse a ese punto tanto por la izquierda como por la derecha. El límite existe si el límite izquierdo y derecho son iguales. El límite, si existe, es único independientemente de si la función está definida en ese punto.

1. LIMITES LATERALES
Para analizar el límite de una función en un punto, es necesario
acercarse a ese punto tanto por derecha como por izquierda, a
esta forma de acercarse al punto analizado por los lados se le
conoce como Límites Laterales y se simboliza por:
De hecho, para poder decir que el límite en un punto existe, se
debe verificar que el límite de f(x) por la izquierda es igual al
límite de f(x) por la derecha.

2. El límite de una función en un punto si existe, es único.
límite tanto por la izquierda como por la derecha
cuando x tiende a 2 es 4.
El límite de la función es 4 aunque la función no
tenga imagen en x = 2.

3. •
En el caso A el límite de f(x) cuando Xo se acerca a 2, es 4, ya que los limites
tanto por la derecha como por la izquierda es 4.
•En el caso B, Xo se acerca a 2 y su imagen se acerca a 2, pero cuando Xo
se acerca por la derecha, se ve que la imagen se acerca a 0. En este caso
las imágenes se acercan a diferentes valores por lo tanto se dice que no
hay un límite cuando Xo se acerca a 2.

6. • Resuelve
a)
2x - 5, si x 3
b) sea f(x)
x - 2 , si x 3

7. 3x 5, si x < -1
c) sea g(x) x 2 1, si - 1 < x < 2
6 - x , si x > 2
Calcular (en caso de existir) cada uno de los límites siguientes:
i) ii) iii)
iv) v) vi)

8. a - 2x, si x < 1
Si f(x) halla " a" para que exista
6 x a, si x 1

9. ax 5, si x < -1
Si h(x) x 2 1, si - 1 < x < 2 halla " a" , " m" para que exista
mx 6, si x > 2

10. x2 x 2 x 2
x 2
Lim x 2 4 x 4 Lim x 2 4x 4
x 2 x 2

11. CONTINUIDAD
Una función se considera continua cuando ser
cumple:

12. 2x - 5, si x 3
sea f(x)
x - 2 , si x 3
• Probar si es continua en el punto 3

13. x 2 - 2x - 5, si x < 0
Si f(x) -7 ,1 x 9
x 16, si x > 9
Analiza la continuidad en los puntos x0 0, x0 9 y x0 11

14. ax - 3, si x 4
Si f(x)
x 1 , si x > 4
Halla el valor de “a” si la siguiente función en continua en x = 4

15. x ;x 1
Dada la función f definida por f(x) ax b, si 1 < x < 4
- 2x1 , si x 4
Halla las constantes a y b para que f sea continua en su dominio