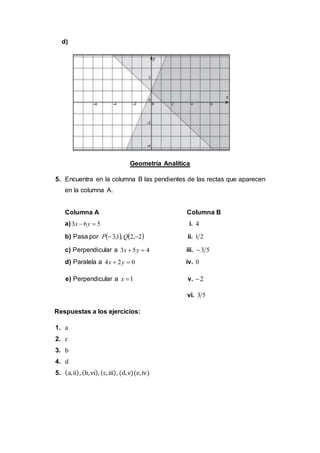
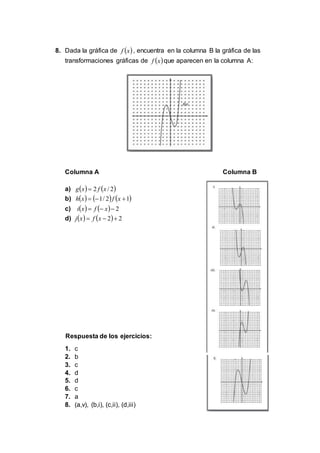
El documento contiene 5 preguntas sobre ecuaciones de rectas, circunferencias, parábolas y elipses. Se pide identificar ecuaciones correspondientes a diferentes figuras geométricas dadas ciertas condiciones, así como encontrar ecuaciones equivalentes. También se incluyen preguntas sobre clasificar figuras y calcular elementos como pendientes, radios y lados de figuras.

1. TRABAJO # 14
Recta
1. Indica la opción que contiene una ecuación de la recta que pasa por los
puntos  1,4 P y  5,2Q .
a) 3 yx
b) 5 yx
c) 3 yx
d) 5 yx
2. Halla la opción que contiene la ecuación general de la recta que es
perpendicular a 1535  yx , y que pasa por el punto  2,9 P .
a) 37573 x
b) 1753  yx
c) 1753  yx
d) 3753  yx
3. Calcula la distancia del punto  1,2P a la recta 586  yx .
a)2
b) 5.2
c)3
d) 5.3
4. Elige cuál de las gráficas representa la región dada por:
xyxy 8.01,12  .

2. a)
b)
c)

3. d)
Geometría Analítica
5. Encuentra en la columna B las pendientes de las rectas que aparecen
en la columna A.
Columna A Columna B
a) 563  yx i. 4
b) Pasa por    2,2,1,3  QP ii. 21
c) Perpendicular a 453  yx iii. 53
d) Paralela a 024  yx iv. 0
e) Perpendicular a 1x v. 2
vi. 53
Respuestas a los ejercicios:
1. a
2. c
3. b
4. d
5. (a,ii), (b,vi), (c, iii), (d,v)(e,iv)

4. Geometría Analítica
1. Indica la opción que contiene la ecuación de la circunferencia con centro
en  3,2 C y radio 4.
a) 0964 22
 yyxx
b) 0946 22
 yyxx
c) 0364 22
 yyxx
d) 0346 22
 yyxx
2. Halla la opción que contiene la ecuación centro-radio de la
circunferencia.
0
4
1
6 22
 yyxx
a)   91
2
3 2
3






 yx
b)  
4
9
2
1
3
2
3






 yx
c)  
4
9
1
2
3 2
3






 yx
d)   9
2
1
3
2
3






 yx
3. Halla la ecuación de la circunferencia de radio 2 que es tangente en el
punto  1,1 P a la recta L: 0134  yx .
a) 4
17
65
17
19
22












 yx
b) 4
17
19
17
23
22












 yx
c) 4
17
19
17
65
22












 yx
d) 4
17
23
17
19
23












 yx

5. 4. Clasifica la circunferencia como real, degenerada o compleja
02612822 22
 yxyx .
a) real
b) degenerada
c) compleja
Circunferencia
5. Encuentra en la columna B las clasificaciones de las ecuaciones que
aparecen en la columna A.
Columna A Columna B
a) 0
36
47
3
4 22
 yyxx i. Circunferencia de radio 4
b) 0
4
17
422
 yyxx ii. Circunferencia compleja
c) 0
4
45
6 22
 yyxx iii. Un punto:  2,21 C
d) 0
4
6322
 yyx iv. Circunferencia de radio 2
v. Un punto:  21,2P
Respuestas a los ejercicios:
1. c
2. d
3. a
4. b
5. (a,iv),(b, iii), (c,ii), (d,i)
Parábola
1. Indica la opción que contiene la ecuación de la parábola con vértice en
 5,2 V y foco  5,0 F .

6. a)    245
2
 xy
b)    245
2
 xy
c)    285
2
 xy
d)    285
2
 xy
2. Halla la opción que contiene la forma estándar de la ecuación de la
parábola:
0
4
5
42
 yxx
a) 












4
1
4
2
1
2
yx
b)  4
4
1
2
1
2






 yx
c) 












4
1
4
2
1
2
yx
d)  4
4
1
2
1
2






 yx
3. Encuentra el lado recto de la parábola que pasa por los puntos
   12,1,19,2 QP y  4,1R .
a) 2
b) 1
c)
2
1
d)
4
1
4. Encuentra en la columna B la ecuación de la parábola dada en la
columna A:

7. Columna A Columna B
a) 742
 xxy i. 












3
1
2
2
1
2
yx
b) 












2
1
4
3
1
2
xy ii. 0
9
19
4
3
22
 xyy
c) 0
24
11
22
 yxx iii.   31
2
 xy
d)   






2
1
11
2
xy iv.   32
2
 yx
v. 1
2
1 2
 yyx
vi.
2
7
2
3
1 2
 xxy
Respuesta a los ejercicios:
1. d
2. c
3. b
4. (a,iv),(b, ii), (c, i), (d,v)
Geometría Analítica
1. Indica la opción que contiene la ecuación de la elipse con focos  1,31 F
y  1,52 F , así como eje mayor de 16 unidades.
a)
    1
48
1
64
1
22



 yx
b)
    1
64
1
48
1
22



 yx
c)
    1
64
1
48
1
22



 yx

8. d)
    1
48
1
64
1
22



 yx
Elipse
2. Halla la opción que contiene la ecuación de la elipse que tiene vértices
     2,5,3,7,3,3  y  4,5  .
a)     1
2
3
5
2
2



y
x
b)
    13
2
5 2
2


y
x
c)
    13
2
5 2
2


y
x
d)     1
2
3
5
2
2



y
x
3. Encuentra la ecuación del lugar geométrico de todos los puntos que
tienen ordenada de 14422
 yx .
a) 1
14416
22

yx
b) 1
916
22

yx
c) 1
169
22

yx
d) 1
16144
22

yx
4. Encuentra la ecuación de la elipse con lado mayor 10, lado menor de 8
y centro en  2,1C .
a)
    1
25
1
16
2
22



 yx
b)
    1
25
2
16
1
22



 yx

9. c)
    1
16
2
25
1
22



 yx
d)
    1
16
1
25
2
22



 yx
Geometría Analítica
5. Encuentra en la columna B la ecuación equivalente que aparece en la
columna A.
Columna A Columna B
a) 036243649 22
 yxyx i.
    1
36
1
9
2
22



 yx
b) 084072436 22
 yxyx ii.
    1
9
3
4
2
22



 yx
c)
    1
9
2
16
3
22



 yx
iii. 02896454169 22
 yxyx
d)
    1
9
2
16
3
22



 yx
iv.
    1
36
5
4
1
22



 yx
v. 025241849 22
 yxyx
vi. 036362494 22
 yxyx
vii.
    1
9
2
16
3
22



 yx
Respuestas a los ejercicios:
1. d
2. b
3. d
4. c
5. (a,ii), (b,iv), (c,iii), (d,vi)

10. Hipérbola
1. Indica la opción que contiene la ecuación del lugar geométrico de los
puntos en el plano cuya diferencia de su distancia a los puntos  0,3P y
 0,3Q es 4.
a) 1
45
22

xy
b) 1
45
22

yx
c) 1
54
22

xy
d) 1
54
22

yx
2. Halla la opción que contiene la ecuación de la elipse que tiene vértices
 0,31V y  2,32V y focos  2,31 F y  4,32F .
a)     1
8
3
1
2
2



x
y
b)     1
8
1
3
2
2



x
y
c)     1
8
1
3
2
2



x
y
d)     1
8
3
1
2
2



x
y
3. Cuál de las siguientes opciones contiene una asíntota de la hipérbola
    1
16
4
4
2
22



 yx
.
a)
4
3
2  xy
b) 82  xy
c) 8
2
1
 xy

11. d)
4
3
2
1
 xy
Geometría Analítica
4. Determina la longitud del lado recto de la hipérbola
    1
8
2
16
3
22



 yx
.
a) 2
b) 3
c) 4
d) 5
5. Encuentra en la columna B la ecuación dada en la columna A.
Columna A Columna B
a)
    1
4
2
4
2
22



 yx
i. 044422
 yxyx
b)
    1
9
3
4
2
22



 yx
ii. 036362449 22
 yxyx
c) 02516643 22
 yxyx iii. 036243649 22
 yxyx
d) 0481243 22
 yxyx iv.
    1
3
1
4
2
22



 yx
v.
    1
3
2
4
1
22



 yx
vi.
    1
3
2
4
1
22



 yx
Respuestas a los ejercicios:
1. d
2. d
3. b
4. c
5. (a,i),(b,iii),(c,v),(d,iv)

12. Funciones
1. ¿Cuál de las siguientes relaciones no es función?
a)         12,4,2/5,3,2,2,2,1 
b)         10,4,10,3,3,2,3,1
c)         12,4,2/5,3,2,1,3,1 
d)         8,6,15,2,0,3,2,15 
2. ¿Cuál de las siguientes gráficas no corresponde a la gráfica de una
función?
3. ¿Cuál de las siguientes opciones corresponde al dominio de la función
cuya gráfica se muestra en la figura?:
a)  ,3
b)  ,4
c)   ,
d)  3,
4. Si    4,62
 xfsssf es:
a) 44142
 xx
b) 40162
 xx
c) 44162
 xx
d) 40142
 xx

13. 5. ¿Cuál es la opción que contiene el dominio y la imagen de la función que
se muestra a continuación?:
a) Dom: R , imagen:   ,2
b) Dom: R , imagen: R
c) Dom:   ,2 , imagen:   ,2
d) Dom: R , imagen:   ,2
6. Un punto  1,2P pertenece a la función  xf . ¿Qué opción contiene el
punto  ?,2Q de la función     ?5 xfxg :
a)  1,7
b)  6,2
c)  4,2 
d)  1,3
7. Si   2
xxf  , ¿Cuál de las siguientes gráficas corresponden a
    ?13  xfxg

14. 8. Dada la gráfica de  xf , encuentra en la columna B la gráfica de las
transformaciones gráficas de  xf que aparecen en la columna A:
Columna A Columna B
a)    2/2 xfxg 
b)      12/1  xfxh
c)     2 xfxi
d)     22  xfxj
Respuesta de los ejercicios:
1. c
2. b
3. c
4. d
5. d
6. c
7. a
8. (a,v), (b,i), (c,ii), (d,iii)