Cuaderno DASO 2008

Escola Universitaria de
Enxeñería Técnica
Forestal

APUNTES DE DASOMETRÍA

Prof. Juan Picos Martín.
Prof. Miguel Á. Cogolludo Agustín. Curso 2.007-2.008

UNIVERSIDADE DE VIGO E.U.E.T. FORESTAL
DASOMETRÍA E ORDENACIÓN DE MONTES

PRIMERA PARTE: DASOMETRÍA
CAPÍTULO 0. INTRODUCCIÓN A LA DASOMETRÍA
0.1. ¿Por qué medir?
0.2. ¿Por qué medir árboles y masas forestales?
0.3. Dasometría y ciencias afines.
0.4. Unidades de medida.
0.5. Normalización de símbolos utilizados en dasometría.
0.6. Cifras significativas.
0.7. Precisión, sesgo y exactitud de los datos.
0.8. Errores.
0.9. ¿Peso o volumen?
0.10. Componentes del árbol.
0.11. La forma del árbol.
0.12. Medición por desplazamiento de fluido.
0.13. Diferencias entre cantidad, valor y precio.

CAPÍTULO 1. MEDICIÓN DE ÁRBOLES: DIÁMETROS Y ALTURAS.
1.1. Medida del tamaño de una sección.
1.2. Parámetros dasométricos básicos.
1.3. Medición de diámetros de los árboles.
1.4. Medición del espesor de corteza, crecimiento diametral y edad del árbol.
1.5. Medición de pendientes.
1.6. Medición de alturas de árboles.
1.7. El Relascopio
1.7. Nuevos aparatos para mediciones forestales.
1.8. Tabla de pendientes.
1.9. Ejercicios.

CAPÍTULO 2. CUBICACIÓN POR TROZAS
2.1. Fórmulas de Cubicación con un número de secciones predeterminado
2.2. Estimación de los defectos en las trozas.
2.3. Reglas madereras

CAPÍTULO 3. CUBICACIÓN DE TRONCOS COMPLETOS
3.1. Método de cubicación de Meyer.
3.2. Tipos dendrométricos
3.2.1. Tipos dendrométricos y curvas de perfil
3.2.2. Funciones de perfil
3.3. Comparación cubicación comercial con los tipos dendrométricos.
3.4. Coeficientes mórficos
3.5. Fórmulas aproximadas
3.6. Tarifas y tablas de cubicación
3.6.1. Tarifas de cubicación.
3.6.2. Tarifas para Inventario Forestal de Galicia (1986)
3.6.3. Tarifas del Segundo Inventario Forestal Nacional (1993)
3.6.4. Tablas de cubicación.
3.7. Ejercicios.


CAPÍTULO 4. MEDICIÓN DE MADERA APILADA
4.1. Introducción
4.2. Unidades. El estéreo
4.3. Coeficiente de apilado:
4.4. Coeficientes de apilado teóricos
4.5. Cálculo del coeficiente de apilado:
4.6. Cálculo del volumen aparente de las pilas
4.7. Cálculo del volumen de madera flejada.

CAPÍTULO 5. ANÁLISIS DE TRONCOS
5.1. Introducción a la epidometría.
5.2. Definición
5.3. Algunas consideraciones sobre la anatomía de la madera
5.4. Modelos de crecimiento
5.5. Metodología
5.6. Ejercicios.

BIBLIOGRAFÍA DE REFERENCIA

AVERY, T. & BURKHART, H. (1994) "Forest mesurations". McGraw-Hill. New York.
DIAZ MAROTO, I.J. (1995) "Evolución de los métodos de ordenación de montes en España : Situación actual".
Universidade de Santiago de Compostela, Escola Politécnica Superior de Lugo, 65 pp.
DIEGUEZ, U. & col. (2003) "Dendrometría" Mundi Prensa – Fundación Conde del Valle de Salazar.
Madrid. 327 pp.
JUNTA DE CASTILLA Y LEÓN (1999). "Instrucciones generales para la ordenación de montes arbolados en Castilla
y León". Junta de Castilla y León, Zamora, 219 pp.
LÓPEZ QUERO, M. & LÁZARO, F. (1993). "El Catastro y la tributación de los bienes inmuebles rústicos". Madrid.
Paraninfo.
MACKAY, E. (1944 y 1949). "Fundamentos y métodos de la ordenación de montes". E.T.S.I.M. Madrid.
MADRIGAL, A.; ÁLVAREZ, J.G.; RODRÍGUEZ, R.; ROJO, A. (1999). "Tablas de producción para los
montes españoles". Fundación Conde del Valle de Salazar. Madrid.
MADRIGAL, A. (1994). "Ordenación de Montes Arbolados". ICONA. Madrid.
MARTÍNEZ, E. (2000). "Manual de Valoración de Montes y aprovechamientos forestales". Mundi-Prensa. Madrid.
PRIETO, A. & HERNANDO, A. (1995). "Tarifas de cubicación e inventario por ordenador". Madrid. Fundación Conde
del Valle de Salazar. E.T.S.I.M.-UPM.
ROJO, A.; MADRIGAL, A.; PÉREZ, A. (1998). "Estructura y contenido de los proyectos de Ordenación de Montes
Arbolados". Editan los autores. Lugo.
ROMERO, C. (1993) " Teoría de la decisión multicriterio: conceptos, técnicas y aplicaciones". Alianza Editorial.
Madrid. 195 pp.
PARDÉ, J. & BOUCHON, J. (1994). "Dasometría. Versión española de “Dendrométrie de L´ecole national
du génie rural des aux et des forêts” ", por Prieto, A. y López Quero, M. Editorial Paraninfo, Madrid. 387
pp.
VANCLAY, J. (1994) "Modelling forest growth and yield. Application to mixed tropical forest" . CAB. Wallingford. 312
pp.

DASOMETRÍA Y ORDENACIÓN DE MONTES

PRIMERA PARTE: DASOMETRÍA

CAPÍTULO 0. INTRODUCCIÓN A LA DASOMETRÍA

0.1. ¿POR QUÉ MEDIR?
0.2. ¿POR QUÉ MEDIR ÁRBOLES Y MASAS FORESTALES?
0.3. DASOMETRÍA Y CIENCIAS AFINES.
0.4. UNIDADES DE MEDIDA.
0.5. NORMALIZACIÓN DE SÍMBOLOS UTILIZADOS EN DASOMETRÍA
0.6. CIFRAS SIGNIFICATIVAS.
0.7. PRECISIÓN, SESGO Y EXACTITUD DE LOS DATOS.
0.8. ERRORES.
0.9. ¿PESO O VOLUMEN?
0.10. COMPONENTES DEL ÁRBOL.
0.11. LA FORMA DEL ÁRBOL.
0.12. MEDICIÓN POR DESPLAZAMIENTO DE FLUIDO.
0.13. DIFERENCIAS ENTRE CANTIDAD, VALOR Y PRECIO.

Página 1


0. Introducción a la Dasometría.

0.1. ¿Por qué Medir?

Cuando se mide un objeto, esencialmente lo que se hace es contar el número de "piezas"
estándar que hacen falta para tener el mismo tamaño que e objeto. Por ejemplo, la longitud de
una piscina olímpica es 50 m porque 50 unidades estándar de un metro colocadas una a
continuación de la otra tendrían exactamente la misma longitud.

Por tanto "Medición" es la determinación de la magnitud de una variable física en relación con
algún estándar como metro, kilogramo, segundo, amperio,... o alguna unidad derivada de estas

¿Por qué Medir?

Las mediciones se llevan a cabo por alguna de las siguientes razones:

a) Aprender algo. En palabras del científico inglés, Lord Kelvin, "Cuando es posible medir
aquello de lo que se está hablando y se es capaz de expresarlo con números, entonces
se sabe algo de ello. Cuando no es posible o no se mide, cuando no se puede expresar
con números entonces el conocimiento sobre ello es insatisfactorio y pobre".

b) Cumplir las obligaciones legales. Lund (1998) enumera un número de Tratados
Internacionales y Acuerdos que obligan a los gobiernos (y a algunas empresas e
individuos) a mantener y proporcionar determinadas mediciones sobre el territorio y los
recursos.

c) Ayudar a los gestores de los recursos a tomar las decisiones adecuadas a sus intereses
particulares y a los intereses generales.

Evaluación cuantitativa (medición) y evaluación cualitativa.

“Cuando tú mides algo lo expresas en números, sabes algo del mismo; pero cuando no puedes
medirlo (o no lo haces), cuando no puedes expresarlo en números, tu conocimiento es magro e
insatisfactorio” (Lord Kelvin)

Las variables cuantitativas son aquellas que podemos expresar numéricamente: altura, edad,
peso, número de hijos. Estas a su vez las podemos subdividir en variables continuas (altura,
peso) o discretas (número de hijos).

Las variables cualitativas son aquellas que expresan un atributo o característica, por ejemplo:
rubio, moreno, etc.

El uso de ambos tipos de variables es necesario para caracterizar las masas y los recursos
forestales. Si bien como nos indica Lord Kelvin para el conocimiento de una cosa la medición nos
provee de un dato más exacto y objetivo de ella.

El uso de una evaluación cualitativa sobre un atributo o una característica que se puede medir
(por ej. evaluar o denominar un árbol como alto o corto) implica un juicio subjetivo y es mucho
más propenso a un sesgo personal y error. Nuestro compromiso como técnicos es eliminar la
subjetividad y restringir el uso de los juicios cualitativos.

Página 2


Sin embargo hay casos en los que es necesaria la intervención de variables cualitativas que
habrán de introducirse siempre de manera que eliminemos al máximo la carga de subjetividad
que conllevan. Por ejemplo, en un inventario en el que se miden daños por afección de una
plaga, las clases en una escala pueden ser leve, moderado o grave. Será deseable que para facilitar
su interpretación y su uso por los equipos de campo se adjunten fotos descriptivas de ejemplos
de lo que se considera es cada clase.

0.2. ¿Por qué medir árboles y masas forestales?

Hay numerosas variables y parámetros que pueden ser medidos en un monte. La elección de
cuáles de ellos han de ser medidos depende de los objetivos finales de la medición, el tiempo y
los recursos (económicos, humanos y materiales) disponibles.

Las razones que nos llevan a plantearnos cuantificar las existencias de un monte pueden ser:

• Medir la cantidad y calidad de las existencias maderables para determinar cuánta madera se
obtendrá al proceder a la corta y como podrá ser clasificada (madera de sierra, de
trituración, etc...).

• Medir la cantidad de biomasa leñosa para determinar la viabilidad de su utilización como
combustible.

• Medir el área foliar para determinar cuántos contaminantes serán interceptados o absorbidos
por luna determinada masa forestal.

• Evaluar y Valorar los daños causados por incendios, insectos, enfermedades, etc para realizar
de forma correcta la conveniencia del tratamiento fitoquímico.

Por ello estaremos interesados en hallar:

El tamaño total de la población (en términos estadísticos).
El tamaño y características medias de un individuo (media, moda y mediana).
El valor esperado de ciertas variables de la población.

Debido a que los árboles son los componentes fundamentales de los montes arbolados las
medidas en los montes conllevarán la medición de ciertos árboles de la misma. Las mediciones se
realizarán en árboles individuales, grupos de árboles (rodales) o grupos de rodales (masa forestal
o monte arbolado). La elección de las variables a medir y de los individuos que se van a medir
(población muestral) es una parte fundamental de la dasometría.

También la elección del equipo de medición es muy importante porque puede influir
decisivamente en la eficacia del trabajo de campo y por tanto en el resultado de las mediciones.
A pesar de ello, el equipo es tan solo uno más de los numerosos costes de ejecución de un
inventario y no debe descuidarse ninguno de cara a obtener un resultado óptimo.

El reto del futuro de los técnicos forestales:
El desarrollo de la evaluación de los recursos forestales en nuestro país ha estado orientado
tradicionalmente hacia los recursos forestales maderables, dejando de lado gran parte de los
recursos forestales no maderables, los recursos naturales asociados a los bosques, los beneficios
ambientales y los ecológicos. Es un reto, por lo tanto, investigar e incluir los aspectos de
evaluación de los demás recursos forestales.

Página 3


El uso responsable de los bosques y otros recursos naturales asociados con ellos (animales,
plantas, suelo, agua) es vital para el bienestar de una nación. Esta necesaria planificación y
manejo de los recursos puede malograrse, a menos que esté disponible una información
cuantitativa confiable sobre la multitud de tópicos relacionados. Tal información se deriva de la
medición.

Medición directa
La evaluación o medición directa está basada en observaciones que se obtienen de forma
inmediata al tomar mediciones o hacer conteos sobre el recurso que nos interesa. Por ejemplo:
cuando empleamos una forcípula (ver más adelante “Instrumentos de medición”) para
determinar el diámetro de un árbol, estamos haciendo una evaluación directa porque el dato
obtenido expresa inmediatamente el diámetro del árbol.

Medición indirecta
La evaluación o medición indirecta se basa en mediciones que nos permiten inferir los datos del
recurso de una manera menos inmediata. Tendremos primero que efectuar cálculos para obtener
el dato que nos interesa sobre el recurso. Por ejemplo: cuando empleamos una fotografía aérea
o una imagen de satélite para evaluar un recurso forestal como puede ser el bosque,
obtendremos datos que nos permitirán conocer o evaluar la condición del recurso indirectamente.

0.3. Dasometría y ciencias afines.

Dasonomía, es definido por la RAE como “Estudio de la conservación, cultivo y aprovechamiento
de los montes”. Etimológicamente procede del griego dasos = bosque, -nomía = conjunto de
leyes o normas. Es una parte de la Ciencia Forestal que trata de la gestión de las masas
forestales y está basada en principios científicos que resultan de la comprensión de la biología del
árbol y de la dinámica de las masas forestales. Se divide fundamentalmente en tres disciplinas:

• Selvicultura: ciencia que se dedica a la creación, cultivo, estudio, conservación y
tratamiento racional de los montes.
• Ordenación de montes o dasocracia (etimológicamente “gobierno del monte”): ciencia
que se ocupa de la planificación y gestión forestal.
• Dasometría.

La Dasometría, llamada en sus inicios Xilometría, es una parte de la Dasonomía que se encarga
de la medición, cálculo o estimación de los volúmenes, edad e incremento de las masas
forestales. En inglés se denomina forest mensuration o bien forest meansurement, y en el
sentido más amplio considera la medida de los montes.

Se puede dividir en las siguientes ramas:

• Dendrometría: estima el volumen de madera y leñas del árbol individual, en pie
o apeado.
• Estereometría: sirviéndose de la anterior, estima las existencias en volumen de
madera y leñas de un conjunto de árboles.
• Epidometría: estima la evolución en el tiempo de las existencias (crecimiento
del árbol o de la masa arbórea) y estudia la producción reglada.

Página 4


Inventario Forestal. Para algunos autores es una rama más de la dasometría, aunque es más
bien un conjunto de técnicas para la recolección de los datos necesarios en dasometría. El
Inventario admite varias definiciones y entre ellas nos quedaremos con la que sigue: "Inventario
Forestal es el conjunto de técnicas y principios que se emplean para caracterizar la situación
pasada y actual del monte, así como su más probable evolución."

Es decir, el Inventario Forestal recopila, organiza y describe de manera fiable, la información
concerniente a los recursos forestales de una zona determinada. El Inventario Forestal se
extiende en su ámbito de aplicación a todos los recursos forestales y no solo a los recursos
madereros por lo que se favorece la vinculación del monte con una amplia gama de usos 1
finales. Por tanto, el Inventario Forestal presenta el monte en todos los aspectos que interesan a
quien va a hacer uso de la información, dando fundamento a las decisiones que afectan a los
recursos forestales (valoraciones, ordenaciones, planificaciones, etc.). Además de la toma de
decisiones, el inventario fomenta el análisis de los recursos forestales.

Página 5


0.4. Unidades de Medida.

España, como firmante de la Metric Convention, ha hecho el compromiso de utilizar el Sistema
Internacional de Unidades (SI). Estas unidades están definidas de forma muy precisa y unívoca
de forma que, por ejemplo un metro en Pontevedra se exactamente igual que un metro en
Australia.

Las unidades básicas del SI son:

Longitud: metro (m)

Masa - peso: kilogramo (kg)

Tiempo: segundo (s)

Corriente eléctrica: Amperio (A)

Temperatura: Grado Kelvin (K)

Intensidad Luminosa candela (cd)

Cantidad de una Substancia mol (mol)

Otras unidades pueden derivarse de la combinación de estas o de la inclusión de prefijos
decimales (ej. centi, deci, kilo,...).

No obstante, en la actividad forestal son usualmente utilizadas y aceptadas algunas unidades, no
incluidas en el SI, como por ejemplo:

Area: hectárea (ha) = 10.000 m2

Tiempo: día (d) = 86.400 s

Tiempo: año (a)= 365—86.400 = 31.536.000 s

Masa: Tonelada (t) = 1.000 kg.

Masa aparente: Estéreo (st)

A lo largo del tiempo, muchas unidades y referencias han sido desarrolladas y usadas. Este
fenómeno ha sido especialmente intenso en las magnitudes relacionadas con el sector primario,
fundamentalmente la agricultura y así tenemos ejemplos como:

Ferrado - Es una unidad tradicional agraria gallega, es teóricamente la superficie de
tierra que se puede sembrar con un ferrado de grano (medida de
capacidad de entre 13,13 y 16,15 l). Varía de unos lugares a otros
(generalmente por parroquias o concellos). En la página siguiente se
muestran los valores para algunos concellos de Galicia.1

1
En la dirección http:/www.dioptra.es/Explorer/servicios/unidades/unidadmedida.php3 es posible consultar una base de
datos de los valores del ferrado en los distintos concellos de Galicia.

Página 6


Cunca- Es la duodécima parte de un ferrado. También llamada conca.

Cuartillo – Es la veinticuatroava parte de un ferrado.

Cupelo- equivale a 21 m2 Es muy usado en Ourense, especialmente en Terra de
Celanova). También llamado Copelo.

En una cita del Catastro de Ensenada1 en la parroquia de San Miguel de Castro (A Estrada) se
puede leer:

“A la nona pregunta (De que medidas de tierras se usa en aquel pueblo, de quantos
pasos...) digeron que en esta dicha feligresia se usa lo medida de tierra que llaman
ferrado el que se divide en doce concas y estas en veinte y quatro quartillos y dicho
ferrado de tierra tiene en cada treinta varas castellanas y de circunferencia ciento y
veinte cada una de quatro quartas; cuyo ferrado de tierra si se siembra de trigo lleva
los tres quartos de dicho de la misma semilla, si se siembra de centeno lleva un
ferrado, si se siembra de lino lleva ferrado y medio de linaza, si se siembra de mijo
lleva quatro quartillos, si se siembra de mijo menudo lleva un quartillo, si se siembra
de nabos lleva medio quartillo y si se siembra de alcacer que suele ser la escoria del
centeno lleva ferrado y medio.”

Las normas y unidades de medidas, incluyen las formas de registrar y expresar los resultados de
las mismas y los símbolos que han de ser empleados.

La tabla de la página siguiente expresa las disposiciones más usuales en lo que respecta a las
unidades empleadas en dasometría. Además se recogen otras normas y disposiciones al respecto.

1
Transcrito por Manuel Reimóndez Portela. “A Estrada Rural”. Diputación de Pontevedra 1990

Página 7


Página 8


Página 9


Página 10


0.5. Normalización de símbolos utilizados en Dasometría
(PARDÉ & BOUCHON, 1994).

Para las variables de uso más frecuente utilizadas en Dasometría se utilizan los siguientes
símbolos normalizados por I.U.F.R.O. (International Union of Forest Research Organizations)

Se usarán en minúscula cuando se refieran a individuos y se usarán en mayúscula cuando se
refieran a masas forestales, bien referidas a la unidad de superficie bien referidas a la población
total.

Símbolo Definición

c Circunferencia.

d Diámetro. En Dasometría se mide normalmente el diámetro normal (el diámetro a
la altura de 1,30 m). Se supone que a esa altura la influencia de las raíces ya se ha
perdido.
dg Diámetro medio cuadrático.
d Diámetro medio aritmético.
dx Diámetro a x metros del suelo.

k, f Coeficiente de forma o coeficiente mórfico.

g Sección normal del árbol (sección a la altura de 1,30 m).

G Área basimétrica de una masa.

h Altura.
hdom Altura dominante.
h Altura media aritmética
hd Altura correspondiente al árbol de diámetro medio aritmético.

i Incremento. Mediante un subíndice se especificará la variable a la que se refiere: id,
incremento del diámetro.

t Edad del árbol.

n Número de árboles.

p, r Crecimiento relativo. Mediante un subíndice se especificará la variable a la que se
refiere.

v Volumen del árbol.

V Volumen de la masa.

Página 11


0.6. Cifras significativas1.

Cuando por ejemplo se cuentan los pies en una parcela de muestreo no existe duda sobre el
número exacto de pies allí existentes (si se ha hecho de forma adecuada); si se han contado 70
árboles serán 70, no 71 ni 72, ni podrá expresarse el resultado con decimales. Esto ocurre
generalmente en el caso de variables discretas, que se suelen medir como números enteros.

Por contra, la mayoría de las variables continuas son aproximadas, por lo que el valor exacto de
una medición simple es desconocido. El último dígito de la medida implica unos límites en la
escala de medida entre lo que se cree el valor verdadero y un valor falso. Si, por ejemplo, con
una forcípula de precisión de centímetros se miden 25 cm, esas dos cifras están garantizadas
como correctas por el aparato con un error absoluto menor al medio centímetro (se puede
asumir que el valor real está entre 24,5 y 25,5 cm), por ello se dice que su número de cifras
significativas es dos.

Las cifras significativas son los dígitos existentes si se lee el número de izquierda a derecha,
empezando por el primer dígito distinto de cero y acabando por el último. Los números 25; 2,5;
0,25 y 0,025 tienen dos cifras significativas, el 2 y el 5. Los números 25,0; 2,50; 0,250 y 0,0250
tienen tres cifras significativas, el 2, el 5 y el 0 de la derecha. Resulta por tanto análogo escribir
25 cm, 2,5 dm ó 0,25 m, pues el número de cifras significativas es el mismo en las tres
cantidades.

Es incorrecto anotar más cifras significativas de las que realmente se han observado; por ejemplo
anotar un diámetro de 25,0 cm al medir un diámetro implica que el aparato empleado tiene una
precisión milimétrica, por lo que el resultado tiene tres cifras significativas (2, 5 y 0); no sería
correcto si el aparato sólo tuviese precisión de centímetros.

No se deben omitir ceros significativos en lugares decimales; por ejemplo se debe escribir 12,0 m
en lugar de 12 m si el cero es una cifra significativa.

En la multiplicación y en la división, el factor con un número menor de cifras significativas limita
el número de cifras significativas en el resultado. En el ejemplo siguiente aparece entre
paréntesis el número de cifras significativas de cada cantidad:

895,67 — 35,9 = 32.154,553
(5) (3) (8) El resultado debería escribirse: 321—102

Esta norma se debe a que 895,67 representa una medida entre 895,675 y 895,665, y 35,9 una
medición entre 35,85 y 35,95. Los productos de estas cuatro combinaciones difieren en todos los
dígitos salvo en los tres primeros, que son los que se deben tomar como cifras significativas.

El número de cifras significativas de un número entero es infinito.

Para determinar el número de cifras significativas en el resultado de una suma o una resta, se
recomienda, en primer lugar, alinear los números de acuerdo con sus decimales. En segundo
lugar, contar los lugares existentes entre el número situado más a la izquierda empezando por la
izquierda y el número más a la izquierda empezando por la derecha, ambos incluidos; ese valor
se corresponderá con el número de cifras significativas del resultado.

Como se ha indicado anteriormente, es muy importante especificar el número de cifras
significativas cuando se anota el resultado de una medición, ya que una serie larga de números
no significativos puede inducir a confusión, pues presupone una precisión en la medida que no se
corresponde con la real.
1
Las pág. 11-15 son extracto del libro “Dendrometría” (2.003) Diéguez et al. FUCOVASA.

Página 12


Teniendo en cuenta que la precisión de los resultados finales está limitada por la precisión de los
datos iniciales, es necesario establecer a priori cuántas cifras significativas se van a considerar en
las medidas. Se debe resaltar que usar una precisión mayor de la requerida supone una pérdida
de recursos (tiempo y dinero), por lo que se debe seguir una serie de recomendaciones:

No se debe intentar hacer mediciones con una precisión mayor (más cifras significativas) a la
permitida por el aparato o procedimiento empleado. Por ejemplo, resultaría ilógico intentar medir
diámetros con precisión milimétrica empleando una forcípula graduada en centímetros.

2. La precisión demandada en los datos iniciales depende del margen establecido para que una
diferencia sea significativa en la comparación de resultados. Por ejemplo, si los resultados de la
aplicación de una serie de tratamientos selvícolas en una masa se van a comparar en términos de
crecimiento en volumen, estableciendo diferencias significativas a partir de 0,1 m3, no es
necesario estimar volúmenes con una exactitud mayor que la décima parte de un metro cúbico.

3. La variación en la población muestreada y el tamaño de muestra inf1uyen en la precisión
elegida para los datos iniciales: si la población es muy heterogénea o la muestra es pequeña, no
merece la pena establecer precisiones muy elevadas, pues no van a repercutir en una mejora
importante en los resultados.

0.7. Precisión, sesgo y exactitud de los datos.

La precisión es un concepto que tiene diferente significado según se defina para una única
medición o para un conjunto de mediciones de un mismo objeto. En el caso de una única
medida, la precisión está relacionada con la unidad más pequeña que se puede distinguir en la
medición, y generalmente se indica con el número de decimales de la medida. Por ejemplo, si
una cinta métrica está graduada en centímetros, la precisión cuando se mide con esa cinta es de
un centímetro.

En el caso de una serie de medidas la precisión es el grado de dispersión de las mismas, es decir,
evalúa hasta qué punto dichas medidas se aproximan a su media. Para cuantificar la precisión se
suele emplear lo que se denomina error estándar; cuanto menor es el error estándar de una
estimación, más precisa resulta. La expresión matemática del error estándar σx es la siguiente:

σx 2= σ 2 / n

donde σ es la desviación típica de las mediciones y n es el número de mediciones.

El sesgo es el valor medio de los errores cometidos en las mediciones de una magnitud. Cuando
se realizan varias mediciones de un objeto esas mediciones son insesgadas si su media coincide
con el valor real. Esto ocurre siempre y cuando no
se cometan errores sistemáticos resultantes de un
método inadecuado de medida, errores en los
aparatos, etc.

Los conceptos precisión y sesgo se pueden ilustrar
con un ejemplo de una diana sobre la que se
realizan seis disparos. La imagen superior izquierda
es precisa (poca desviación de los disparos con
respecto a su media) e insesgada (su media
coincide en el blanco). La imagen superior derecha
es precisa pero sesgada (su media no coincide en

Página 13


el blanco). La imagen inferior izquierda es poco precisa (mucha dispersión de los disparos con
respecto a su media) e insesgada (la media coincide en el blanco). Por último, la imagen inferior
derecha es poco precisa y sesgada.

La exactitud de una serie de mediciones aúna los conceptos de precisión y sesgo. Una serie de
mediciones que sean precisas e insesgadas dan lugar a un valor medido exacto. La exactitud de
una medición se puede estimar a partir de la siguiente expresión (Bruce, 1975):

Exactitud = sesgo 2 + precisión 2

Una medida exacta es aquella en la que los errores sistemáticos y aleatorios son pequeños,
mientras que en una medida precisa sólo es pequeño el error aleatorio. Las medidas precisas
pueden no resultar exactas debido al sesgo. Por ejemplo, supóngase que se realizan tres
mediciones del diámetro de un árbol con los siguientes resultados: 35 cm, 35 cm y 35 cm. Si el
diámetro real es de 30 cm, las mediciones hechas son precisas (no existe diferencia entre cada
una de las mediciones y la media de las mismas, 35 cm), pero no exactas, pues el valor medido
(35 cm) difiere del valor real (30 cm). Esto indica que las mediciones están sesgadas.

Por otra parte, de la ecuación anterior se deduce que si el sesgo es nulo, precisión es sinónima
de exactitud.

Cuando se realizan mediciones de un objeto 110 tiene sentido hacerlas con una precisión mayor
que la demandada para su posterior uso. De igual manera, la precisión de las medidas realizadas
en campo no debe ser menor que la requerida para el tratamiento de datos previsto.

0.8. Errores.

Todos los procesos de medida llevan asociados una cierta imprecisión. Por este motivo, el
resultado de una medición debe incluir el valor obtenido, la unidad de medida y un número,
denominado error, que es un indicador del grado de imprecisión de dicha medida. Los errores
que se cometen en las mediciones son desconocidos, pero pueden estimarse y acotarse, siempre
y cuando se conozca la causa que los provoca. El conocimiento de las posibles fuentes de error
cuando se realiza una medición permite establecer unas normas a seguir para minimizarlos en 10
posible y determinar el grado de confianza de dicha medición.

Cuando se va a realizar una medición es imprescindible fijar qué error máximo se puede tolerar.
Esta tolerancia de error debe ser tenida en cuenta tanto por la persona que efectúa las
mediciones como por la persona que va a usar esa infoffi1ación. El conocimiento del error
máximo admisible permite una selección adecuada de los métodos a emplear en la medición.

Otro aspecto de gran importancia es el conocimiento del orden de magnitud de las variables con
las que se trabaja. Así, será necesario tener presente que, por ejemplo, un volumen por hectárea
de 400 m3 puede ser cierto para una determinada masa forestal en unas condiciones
estacionales concretas, mientras que para ese mismo lugar un volumen total de 4.000 m3 es un
valor a todas luces erróneo. Por tanto, las operaciones aritméticas comunes (suma, resta,
multiplicación y división) deben realizarse sin error, incluso aunque se utilicen computadoras para
su cálculo.

La magnitud del error se puede expresar en términos absolutos o en términos relativos. El error
absoluto se suele nombrar con la letra E con un subíndice que indica la variable que se está
midiendo (Evariable medida). Su valor es la diferencia entre la medida real y la medida observada con
el aparato empleado en la medición. Por tanto, si se considera una variable x cuyo valor real es x
y cuyo valor medido es x', el error absoluto de la variable x es:

Página 14


Ex = x – x'

El error absoluto se expresa en las mismas unidades que la magnitud medida. Si el valor real es
mayor que el medido, se produce un error por defecto y el error absoluto tiene signo positivo (Ex
= x - x'> 0). En caso contrario, es decir, si el valor real es menor que el medido, se produce un
error por exceso y el error absoluto tiene signo negativo (Ex = x - x'< O).

Por ejemplo, si el diámetro de un árbol mide en realidad 30 cm, pero la medición efectuada es de
28 cm, se ha cometido un error por defecto Ed = 30 - 28 = 2 cm. Si en otra medición se
obtuviese un valor para el diámetro de 32 cm, el error sería por exceso Ed= 30 - 32 = -2 cm.

El error relativo se nombra con la letra e y el subíndice correspondiente a la variable que se mide
(evariabie medida). Este valor da una idea de la cuantía del error en relación con la magnitud medida.
Se expresa en tanto por ciento y no tiene unidades. Como en el caso del error absoluto, también
puede cometerse por defecto o por exceso. Si Ex es el error absoluto de la variable x, cuyo valor
real es x y cuyo valor medido es x', entonces la expresión matemática del error relativo es:

Ex valor _ real − valor _ medido x − x'
ex = ⋅100 = ⋅100 = ⋅100
x valor _ real x

En los ejemplos comentados al hablar del error absoluto, el en error relativo sería de un 6,7 % en
ambos casos, aunque en el primero sería por defecto y en el segundo por exceso.

Dos mediciones pueden tener el mismo error absoluto y diferente error relativo, de modo que la
importancia del error absoluto puede ser muy grande en un caso y despreciable en el otro. Por
ejemplo, si en la medición de un árbol de 2 m de altura se comete un error absoluto de 0,5 m, el
error relativo sería del 25 %; en cambio, si se mide un pie de 20 m y se sigue cometiendo el
mismo error absoluto, el error relativo sería sólo del 2,5 %. Por tanto, el error relativo es mejor
indicador de la magnitud del error que se comete al realizar una medición.

Tipos de errores
Los errores se pueden clasificar en cuatro grupos: equivocaciones, errores aleatorios, errores
sistemáticos y errores de muestreo.

Las equivocaciones son errores causados directamente por el factor humano, por ejemplo, al
realizar una lectura incorrecta, emplear un instrumento inadecuado, anotar una cantidad
diferente a la medida o cometer un error en los cálculos aritméticos.

Son errores que se pueden y deben evitar, algunos de ellos de una forma tan sencilla como
realizando la misma lectura más de una vez. Controlar este factor supone una mejora en la
precisión del resultado final.
Los errores aleatorios, también denominados "accidentales", son inevitables y se deben a
numerosas causas imprevisibles que dan lugar a diferentes resultados cuando se repite la medida
en condiciones idénticas. También se pueden considerar como tales las diferencias observadas al
medir la misma magnitud por diferentes métodos o con diversos aparatos.

Son errores fruto del azar, de tipo aleatorio, y se pueden deber a condiciones ambientales no
constantes, limitaciones o deficiencias de los aparatos, etc. Responden a distribuciones
probabilísticas y pueden analizarse por métodos estadísticos (teoría de errores). Por tanto, son
errores que se cometen en las dos direcciones con respecto a la medida real, es decir, unas
veces por exceso (el valor medido es mayor que el real) y otras por defecto (el valor medido es
menor que el real). Este tipo de errores se puede minimizar con la repetición de las mediciones,
pues se van compensando los cometidos por exceso con los cometidos por defecto.

Página 15


Los errores sistemáticos son errores que se cometen siempre por exceso o siempre por defecto
respecto a la medida real, por lo que suponen la existencia de un sesgo en las mediciones. Se
trata de errores que no se compensan entre sí aunque se aumente el número de repeticiones de
una medición. Se deben a causas fijas que provocan una desviación de la interpretación correcta
de una magnitud medida. Las causas más comunes de errores sistemáticos son:

• Aparatos de medida mal calibrados. Por ejemplo, una forcípula con el origen o el intervalo de
medida equivocados, o una cinta métrica 5 cm más corta de lo normal.

• Aparatos sensibles a las condiciones meteorológicas. Un ejemplo de este tipo de errores es el
que se cometería con una cinta métrica que se dilatase por efecto del calor, por lo que todas
las mediciones realizadas con ella llevarían asociado un error por defecto. Así, si la distancia
medida a un árbol fuese de I8 m, la distancia real sería menor.

• Imprecisiones en el método de seleccionar la muestra. Por ejemplo, si en algunas parcelas se
incluyen los árboles del borde y en otras no.

• Incumplimiento de las hipótesis asumidas para la aplicación de los métodos de medición o de
muestreo.

Los errores sistemáticos son muy importantes porque, a no ser que se conozca la causa que los
provoca, son difíciles de detectar. En la práctica, la Única forma de minimizados es realizar
revisiones continuadas de los aparatos a emplear y de las hipótesis asumidas. Estas revisiones
deben ser previas a iniciar las mediciones y periódicas durante el desarrollo de las mismas.
Además, debe prestarse especial cuidado en el uso de los aparatos y en la aplicación de los
métodos. La eliminación total de los errores sistemáticos puede resultar muy costosa, y se debe
de valorar en cada caso el efecto y la repercusión de los mismos.
El error de muestreo está asociado al método empleado para la selección de muestras. La
magnitud de este error se puede estimar a partir de la varianza de la población y del tamaño de
la muestra. La forma de minimizado es objeto de otra disciplina: el Inventario.

Página 16


0.9. ¿Peso o Volumen?

La historia del desarrollo de las técnicas de medición de la madera muestra claramente que los
cambios reflejan los diferentes usos históricos de la madera y la evolución de la de demanda de
la industria forestal.

Obviamente las unidades de medidas que se tomen de referencia deben estar en función del uso
de las medidas y del futuro uso de la madera.

Cuando la madera era manipulada en piezas de sección cuadrada, el volumen de las trozas se
estimaba en función del número de unidades de esas piezas que podría ser obtenido. Cuando el
aserrado evolucionó los aserraderos produjeron una gran variedad de medidas para evaluar las
trozas y los productos que de ella se podrían obtener.

Ejemplo de este tipo de medias son el palmo, muy utilizado en Ourense para madera de pino; el
metro a la cuarta real -utilizado en el País Vasco- y el Board Foot, empleado profusamente en
EEUU.

Actualmente, buena parte de la madera es triturada, astillada e incluso sus fibras son separadas
y posteriormente reconstituidas como tableros de partículas, fibras o papel. Por ello estas
medidas y reglas son irrelevantes y sesgadas.

Si exceptuamos los trabajos de investigación, la madera se evalúa con los siguientes propósitos:

• Obtención de un valor de referencia para la compraventa.
• Aportación de información al propietario o al gestor del monte acerca de las existencias y
los cambios de estas.
• Seguimiento y control más exacto del proceso productivo de las fábricas de primera
transformación de la madera. Este mejor control permite una gestión más eficaz y un
mejor conocimiento del proceso productivo y su rendimiento.
• Control y gestión del Parque de Maderas de una fábrica.

Los dos parámetros usados de manera más generalizada son el peso y el volumen.

Ambos parámetros solo pueden ser relacionados, para cada caso, cuando se conoce la densidad
de la madera.

Página 17


Ventajas e Inconvenientes de medir madera por peso o por volumen.

Volumen

Ventajas

• La mayor parte de los estudios e inventario han usado este parámetro.

• Mide lo que el fabricante de fibra o pasta de papel quiere comprar y refleja su valor.

• La madera en pie y apilada puede ser medida en las mismas unidades,
independientemente del tiempo transcurrido desde la corta.

• La cubicación de los lotes de corta puede ser medida en pie por el supervisor de las
operaciones.

Inconvenientes

• El volumen no puede ser fácilmente medido de forma directa. Es necesario una
báscula de densidades de gran tamaño para realizar muestreos adecuados.

• Las estimaciones del volumen pueden tener diferentes grados de precisión, la
comparación solo es posible y creíble cuando los procedimientos de estimación están
estandarizados y son comunes.

• La relación entre el volumen y el peso cambia en las diferentes épocas del año e
incluso en diferentes alturas del fuste de un mismo árbol, el porcentaje de corteza,
etc.

Peso seco

Ventajas

• Mide lo que el fabricante de fibra o pasta de papel quiere comprar y refleja su valor.

• Pone el acento en la bases de valoración de la industria que va a transformar esa
madera.

Inconvenientes

• Solo puede ser estimada indirectamente (bien por predicción o por muestreo) a
partir del peso en verde o el volumen.

• Los costes de muestreo ya que la densidad básica de la madera puede variar con la
especie, la edad, la tasa de crecimiento, la estación, la posición en el árbol, el
porcentaje de corteza, presencia de defectos (madera de reacción, nudos, etc.).

• La combinación de la madera extraída media por peso seco y la masa forestal
remanente en pie, hacen que el registro y la predicción de los cambios de las
existencias, sea impreciso y difícil.

Página 18


Peso en Verde

Ventajas

• Rápida medición con un cose variable muy bajo por cada carga entregada. Los
procesos de medición de la de madera pueden ser automatizado y diseñado para ser
impreso.

• La medición es directa (por ejemplo, con el uso de una báscula de camiones).

• Los resultados de las mediciones sucesivas del mismo lote se espera que sean
coherentes.

• Basar los precios de entrega de madera en el peso, conduce a los productores y
distribuidores a entregar la madera recién cortada. Esto beneficia a las fábricas ya
que la madera llega sin azular o se debe emplear menos energía para triturar
madera verde.

Inconvenientes

• Las básculas son inversiones caras de realizar y mantener.

• La localización de las básculas puede ser lejana al monte. Alguna madera puede ser
sacada del monte y nunca pesarse. Es difícil relacionar los pesos de las extracciones
con el número de árboles apeados o el volumen en pie.

• El distinto contenido de agua en la madera y la diferente de la densidad básica entre
especies son fuentes de variación que hacen que los precios para lotes diferentes
sean difíciles de comparar.

• La combinación de la madera extraída por peso con los datos de la madera que
queda en pie hacen difícil la predicción de los crecimientos y cambios en las
existencias.

• Cuando las raíces son extraídas con los fustes (método del árbol completo) los pesos
son distorsionados por la presencia de tierra, piedras, etc..

Conclusiones

Las básculas donde realizar la medida de los camiones con madera son instalaciones
generalmente disponibles tanto para el comprador como para el propietario que vende.
Es una unidad que hasta ahora ha ganado la confianza del propietario por su rapidez y
por ser fácil de repetir. Más conveniente para el propietario o gestor forestal es el
volumen. El gestor debe diseñar un muestreo fiable para asegurar una correcta
transformación de unidades de volumen a peso para que los cambios en las existencias y
la predicción de los crecimientos puedan ser analizados. No obstante, en aquellas áreas
donde un buen muestreo de la densidad no es posible o adecuado a las condiciones de la
venta, el peso verde ha de ser el parámetro elegido.

Página 19


Cuestiones

1) Una empresa en Portugal paga por cada m3 sin corteza de eucalipto entregado en el
parque de fábrica un precio de 45 €. Por otra parte una fábrica en Galicia paga por cada
tonelada con corteza entregada en su parque a un precio de 34,25 €.

¿Cuál es el mejor precio, sabiendo que en la fábrica gallega el densímetro ha marcado 1080
kg / m3 c.c. y que el porcentaje de corteza es del 18%?

Portugal = 45 € / m3 sc Galicia = 34,25 € / t cc

45 € / m3sc ≡ 45 * 0,82 € / m3cc ≡ 36,96 € / m3cc

36,96 € / m3cc ≡ 36,96 ÷ 1,080 € / t cc ≡ 34,16 € / t cc

Luego el precio es mayor en Galicia (un 0,2 % más)

2) El precio de un estéreo de Eucalyptus globulus descortezado es de 20 euros.

Se sabe que:
• El coeficiente de apilado de la madera es de 0,72
• La densidad básica es de 0,74 g/cm3
• El contenido de humedad es en la pila es del 80%
• La corteza supone un 15 % en volumen.

Y que una manera de relacionar la densidad de la madera a distinta humedad es
 (1 − v ) ⋅ (H 1 − H 2 ) 
D´H 2 = D´H1 1 − 
 100 
donde DH1 = densidad de la madera a la humedad H1
v = contracción volumétrica de la madera expresada en tanto por uno
(en el caso del eucalipto v puede considerarse v=21)

Se pide:

a) Calcular el precio equivalente de la tonelada sin corteza.

b) Calcular el precio equivalente del metro cúbico con corteza.

Página 20


a)
f = 0,72 es decir que por cada m3 aparente hay un m3 de madera
es decir en este caso 1 estéreo s.c. = 0,72 m 3 s.c. = 20 ∈
20
por tanto 1 m 3 s.c. = = 27,77 ∈
0,72
además 1 m3 s.c.12% = 740 kg

 (1 − 0,21) ⋅ (80 − 12 )  3 3
Por la fórmula D´80% = 0,740 1 −  = 1,1375 g/c = 1,1375 t/m
 100 
luego 1 m s.c. 80 % = 1.137 kg = 27.77 ∈
3

27,77
luego 1 tonelada s.c . = = 24,42 ∈
1,137

b)
Si de 1 m3 c.c. se obtienen 0,85 m3 s.c y 1 m 3 s.c. vale 27,77 ∈

entonces 1 m 3 c.c. = 27,77 ⋅ 0,85 = 23,60 ∈

Página 21


0.10. Componentes del árbol.

Raberón
o
Punta

Fuste
Maderable

Ramas Gruesas
Ø>7,5 cm Ramas Finas
Ø<7,5 cm

Tocón

Gruesas Ø>7,5 cm

Raíces Medias 2,5 < Ø <7,5 cm

Finas Ø<2,5 cm

Raberón + Fuste Maderable = Tronco Completo o Tronco.
Tocón + Raíces = Cepa.

Página 22


0.11. La forma del árbol.

El diámetro del fuste de un árbol generalmente decrece o estrecha desde la base a la punta. La
manera en la que este decrecimiento tiene lugar, en cuanto a la rapidez o a las siluetas que
define, establece la forma del tronco.

Comprender la forma de los árboles induce a:

• Una mejora de la estimación del volumen del fuste o la biomasa de los árboles.

• Una mejora de la estimación de la cantidad de productos que se obtendrán del árbol y su
clasificación por usos posibles.

• Una mejora de la comprensión acerca de los fenómenos de competencia y condiciones de
crecimiento del árbol.

La forma de los árboles es muy compleja. Algunas formas geométricas pueden aproximarse a
distintas partes del fuste de un árbol, pero hay muchas inflexiones e irregularidades. Las especies
y el genotipo predisponen al tronco para adquirir determinadas formas, pero existe un importante
rango de factores medioambientales que pueden influenciar esta forma.

Existe una compleja relación entre la forma del fuste y la copa del árbol. Por esto cualquier factor
que influencie la copa influenciará la forma del fuste.

Si la altura de la copa es pequeña con relación a la altura del árbol, se tendrá árboles de forma
muy regular (cilindro, paraboloide). Por el contrario, si la copa está muy desarrollada como en los
árboles aislados, se tendrán formas de fuste tendiendo hacia el cono. Diferentes partes del
tronco crecen con distinta velocidad en función de la influencia del os factores medioambientales
y la distribución de la actividad fotosintética.

Página 23


Adansonia grandidieri, especie de baobab endémica de Madagascar y uno de los
símbolos de la isla. Llega a medir 25 metros de altura y 3 de diámetro. La belleza
de estos ejemplares radica en su especial silueta.

El sueño de los científicos
que trabajan en mejora
genética de especies
forestales sería conseguir
una sección cuadrangular
que permitiera optimizar el
aserrado y disminuyera los
costes de transporte y
apilado.
Además las mediciones y los
cálculos de volúmenes serían
más fáciles. ☺

Página 24


0.12. Medición por desplazamiento de fluido.

El método denominado "de desplazamiento de fluido" o "xylometría", mide de forma muy exacta
el volumen de un árbol o su densidad. Esencialmente consiste en cortar el tronco en trozas
manejables y sumergirlas en un recipiente con un determinado fluido. La cantidad de agua
desplazada es igual al volumen de cada una de las trozas y su suma representa el volumen total
del árbol.

Este método no necesita ninguna
suposición acerca de la forma del árbol
o de las trozas y por tanto ninguna
base teórica más que el principio de
Arquímedes. Una variante de este
método es la denominada “Báscula de
densidad” usada para determinar
densidades en la recepción de madera
en fábricas y que se está imponiendo en
los centros de recepción de la península.

0.13. Diferencias entre cantidad, valor y precio.

Cantidad es una propiedad de los objetos que puede se medida con un número. Puede ser
continua, como el área de un polígono, o discreta como los árboles de un bosque.

Valor es una cualidad de las cosas que mide el grado de utilidad o aptitud para satisfacer las
necesidades o proporcionar bienestar. Puede ser económica o no, e incluso en el caso de ser
económico puede no coincidir con el precio.

Precio es el valor económico en la venta de una mercancía, para que exista un precio (tal y
como se entiende a los efectos de este curso) es preciso que exista un mercado y una
transacción.

Al medir un monte la dasometría nos ayuda a determinar de manera adecuada la cantidad de
madera presente. Para estimar un valor (maderable) es necesario que además podamos
discriminar esa cantidad según las utilidades que puede tener para la industria (apeas, rollizo,
rolla). El precio de venta de ese lote de madera vendrá determinado por el valor económico que
alcancen en el mercado estos productos en la región y en un momento dado.

Página 25


PRIMERA PARTE: DENDROMETRÍA

CAPÍTULO 1. MEDICIÓN DE ÁRBOLES: DIÁMETROS Y
ALTURAS.

1.1. Parámetros dasométricos básicos.
1.2. Medida del tamaño de una sección.
1.3. Medición de diámetros de los árboles.
1.4. Medición del espesor de corteza, crecimiento diametral y edad del árbol.
1.5. Medición de pendientes.
1.6. Medición de alturas de árboles.
1.7. El Relascopio.
1.8. Nuevos aparatos para mediciones forestales.
1.9. Tabla de pendientes.
1.10. Ejercicios.

Página 25


1. MEDICIÓN DE ÁRBOLES: DIÁMETRO Y ALTURA

1.1. PARÁMETROS DASOMÉTRICOS BÁSICOS

Los objetivos de las mediciones son diversos pero generalmente el más destacado es estimar el
volumen y el crecimiento de la masa forestal. Los parámetros de la masa forestal se calcularán
por agregación de los volúmenes y crecimientos de los árboles individuales. Además las
mediciones pueden tener como objetivos el estimar las calidades de estación, realizar modelos
decrecimiento para simular la evolución o el estado de la masa, etc.

Existen gran número de parámetros forestales posibles a estimar, en función de los objetivos
propuestos para las mediciones a realizar. Pero como parámetros básicos podemos citar los
siguientes:

• Diámetro a una altura estándar o a una o varias alturas determinadas.
• Altura, principalmente total o de fuste.
• Espesor de corteza.
• Crecimiento diametral.
• Dimensiones de copa.
• Edad.

Todas estas variables se utilizan porque son sencillas y económicas de medir, y están muy
relacionadas con el volumen, el crecimiento y otros parámetros de la masa forestal. A partir de
ellas se pueden estimar otras de forma más o menos sencilla.

1.2. MEDIDA DEL TAMAÑO DE UNA SECCIÓN

1.2.1. DEFINICIONES. PRINCIPIOS.

La variable más común y más importante en Dasometría es el diámetro del árbol. El tamaño de
un tronco es absolutamente relevante para cuantificar el material leñoso producido, la biomasa
producida o el carbono fijado. Además el diámetro está muy relacionado con otros importantes
parámetros forestales e incluso puede ser un estimador de la calidad de la estación.

Aunque lo que generalmente nos interesa saber no es el diámetro sino el área de la sección
transversal para poder estimar el volumen. Si bien son el diámetro o la circunferencia los
parámetros que serán más fáciles de medir.

Para permitir la comparación de las medidas tomadas sobre distintos árboles o sobre el mismo
árbol en distintos momentos, debe definirse un punto de referencia en el tronco. Es importante
que este punto se sitúe a una altura conveniente cerca del suelo para permitir fácilmente la
localización para su medición por distintos operarios o en distintos momentos.

La convención universal es medir el diámetro, con corteza a menos que se especifique lo
contrario, a una altura fija desde el nivel del suelo. Esta altura estándar es la altura del pecho1.
Esta localización varía ligeramente entre algunos países, En la Europa continental, Australia,
Reino Unido, Canadá, entre otros se considera la altura del pecho definida como 1,30 m de altura
desde el suelo. En Nueva Zelanda, India, Malasia, Sudáfrica y algunos otros países la altura del

1
Se puede ver representado por sus iniciales DAP, o bien llamado diámetro normal (dn). En la
bibliografía escrita en inglés se denomina usualmente Diameter at Breast Height (DBH).

Página 26


pecho se considera como 1,40 m desde el suelo. En Estados Unidos se usa 4,5 pies (1,3716 m) y
en Japón (1,25 m).

Estas alturas son relativamente cómodas, como posteriormente veremos, para la medición con
forcípula y están algo alejadas de la influencia del ensanchamiento que se produce en la base del
árbol (aunque probablemente sería preferible una altura mayor).

La "altura del pecho" es una convención de larga tradición y uso en la práctica forestal. No
obstante se usan en casos muy específicos otras alturas de referencia. Algunos investigadores en
sistemas silvopastorales y agroforestales usan 0,3 ó 0,7 m sobre el suelo como altura de
referencia, debido a que tiene una fuerte correlación con las estimaciones de competencia ente
hierba - cultivo - árbol. Otros investigadores han descubierto que a efectos de calcular el volumen
de un árbol es mejor utilizar alturas relativas en lugar de alturas absolutas. Esto es, por ejemplo
calcular los diámetros a un 5% de la altura total, lo que dará una altura de medición de diámetro
distinta para cada árbol.

1.2.2. DETERMINACIÓN DEL DIÁMETRO. METODOLOGÍA Y CRITERIOS A SEGUIR.

Al medir el DAP es deseable atenerse a normas precisas, las que lamentablemente no están del
todo estandarizadas. Emplear un bastón, una vara, un jalón o cualquier instrumento que permita
determinar este punto sobre el árbol. Si las mediciones no requieren de gran precisión incluso
una marca en la ropa en función de la altura del operario puede ser de gran utilidad.

En parcelas permanentes, en las que se van a realizar varias mediciones separadas en el tiempo,
la altura de medición debe señalarse de forma clara e inequívoca, para lo que se suele pintar una
T invertida (⊥) a 1,30 m del suelo.

Por ejemplo en terreno con pendiente la altura del DAP (1,30 m) se acostumbra a medir ya sea
sobre el nivel medio del suelo en la base del árbol o sobre el nivel en el lado de arriba de la
pendiente. En caso de haber deformaciones del fuste a la altura del pecho la medición puede
desplazarse hacia arriba o hacia abajo o se puede tomar el promedio de dos mediciones.

Árboles inclinados. El DAP para los árboles que tengan el fuste inclinado se marca
perpendicularmente al eje del árbol, con 1.3 m como la distancia más corta sobre el suelo
paralela al fuste.

Bifurcaciones. Cuando la bifurcación ocurra por debajo de la altura del DAP, las ramas se
consideran como dos árboles separados y se marcan individualmente.

Engrosamientos. Si se presenta una anormalidad en el fuste a la altura del DAP (ensanchamiento,
tumor, bifurcación), se marca a la altura inmediatamente inferior en que la sección
transversal es mínima. Si el ensanchamiento permite realizar dos mediciones equidistantes,
por encima y por debajo del mismo, se haría la media cuadrática.

Página 27


El impresionante ahuehuete
(Taxodium mucronatum) del
cementerio de Santa María de
Tule, situado a 12 km de la
ciudad de Oaxaca (México),
mide:

• 14,36 m de diámetro,

• 41 m de altura,

• 36 m de circunferencia,

• 54 m de circunferencia
con sinuosidades.

Se le estiman 2.000 años de
antigüedad.

Algunos investigadores apun-
tan que este Taxodium, está
formado por tres árboles que
se han fusionado, pero
realmente no está demos-
trado.

El Abuelo de Chavín es este
ejemplar de Eucalyptus globulus
Labill. que se encuentra en O
Souto da Retorta (Viveiro, Lugo)
lugar declarado monumento
natural por la Xunta de Galicia en
2000. Fue plantado en la década
de 1880 por Jaime Basols, el
resto de los grandes eucaliptos de
Chavín fueron fruto de sucesivas
plantaciones hasta 1912.

El Abuelo, que es el ejemplar más
emblemático, mide 7,5 m de
grosor troncal y 70 m de altura
pero no es el más alto de este
Souto.

En el Pazo de Rubianes
(Vilagarcía de Arousa, Ponteve-
dra) se encuentran 13 eucaliptos
espectaculares, el mayor de ellos
cuenta con 42 m de altura y 12 m
de grosor.

Página 28

1.2. PARÁMETROS DASOMÉTRICOS BÁSICOS

1.3. MEDICIÓN DE DIÁMETROS EN LOS ÁRBOLES


• CINTA DIAMÉTRICA:

Una cinta diamétrica mide el diámetro de
forma indirecta a partir de la medición
directa de la circunferencia.

Generalmente la cinta aparece rotulada con
una medida de longitud normal (mm ó cm)
por una cara, mientras que por la otra
aparece esa misma escala dividida entre π.

De esta manera al rodear el árbol por su
sección normal por la primera cara
podríamos leer el valor de la circunferencia mientras que por la segunda podemos leer
directamente el valor del diámetro equivalente con ese perímetro.

circunferencia
circunferencia = π ⋅ diámetro diámetro =
π
La cinta debe ser sostenida firmemente pegada al árbol y suficientemente tensa pero evitando
tensarla mucho para que no se produzcan deformaciones de la misma a largo plazo.

Generalmente las cintas diamétricas vienen provistas de un gancho o un pequeño clavo en su
extremo, de forma que sea posible fijar el extremo en árboles de gran diámetro mientras se
rodea el mismo.

Otros modelos se basan en los flexímetros de recogida automática, permitiendo que para
diámetro de menos de 50 cm aumente espectacularmente la velocidad de medición.

La cinta debe rodear al árbol en un plano perpendicular su eje.

Se ha de ser cuidadoso de no realizar las mediciones con la escala boca abajo, en ese caso es
muy frecuente confundir los decimales X,4 por X,6; X,3 por X,8 etc.

Página 33


• RELASCOPIO DE BITTERLICH:

Este aparato, dendrómeto de usos múltiples, será explicado detenidamente en el apartado 1.7.
Este aparato puede ser usado para la medición de diámetros a distintas alturas del fuste y
además permite medir alturas e incluso cubicar un árbol en pie.

Telerrelascopio. Este es un
instrumento de enorme precisión
destinado fundamentalmente a
trabajos de investigación.

Su funcionamiento y sus principios son
iguales que los del relascopio pero
integra un aumento óptico de x 5.

• PENTAPRISMA DE WHEELER:

También conocido como forcípula óptica, este aparato permite medir diámetros de árboles,
estacionándose a cualquier distancia de los mismos. Se compone de dos prismas de cinco caras,
uno de los cuales es fijo. El otro se desliza dentro de un tubo metálico; el campo ocular está
dividido horizontalmente es dos; en la mitad superior, se tiene una imagen del árbol en visión
directa; en la mitad inferior, se tiene una imagen desplazada según cuatro reflexiones (ver
gráficos de la página siguiente). El aparato está diseñado de tal forma que la visual a través de
los dos prismas y la visual directa sean paralelas. El desplazamiento entre las dos imágenes es,
por tanto, igual a la distancia entre el prisma fijo y el móvil. Cuando se llega en el campo a
ocular, por el desplazamiento del prisma móvil, a obtener que el lado izquierdo del árbol esté en
visión directa en la prolongación del lado derecho en visión desplazada, entonces la distancia
entre los prismas s igual al diámetro del árbol.

Es algo aparatoso ya que además del pentaprisma es conveniente un trípode para estacionarlo.

Página 34


OJO

Pentaprisma Móvil

Pentaprisma Fijo
Visual directa por encima del pentaprisma fijo
Visual reflejada a través de los pentaprismas

DIÁMETRO
DEL TRONCO

Página 35


LECTURA AVANZADA

COMPARACIÓN ENTRE EL USO DE CINTA DIAMÉTRICA Y FORCÍPULA PARA LA
MEDICIÓN DE DIÁMETROS EN PUNTOS ACCESIBLES DEL ÁRBOL.

Las forcípulas y las cintas métricas (bien con escala diamétrica - π bien con escala de métrica
normal para medir perímetros) son instrumentos más exactos y rápidos que aquellos basados en
mediciones a distancia mediante instrumentos ópticos (Pentaprisma, Relascopio,
Telerrelascopio,...).

Por ello si los puntos de medición son accesibles (ej. diámetro normal o diámetro tocón) la
elección se suele hacer entre estos dos instrumentos. Generalmente carece de sentido hablar del
uso de las cintas diamétricas en puntos no accesibles del árbol, mientras que determinadas
forcípulas (ej. la finlandesa) pueden usarse acopladas a pértigas para medir diámetros en altura.

SESGO:

Si el árbol tiene una sección aproximadamente circular, no se producen errores significativos con
ninguno de los dos instrumentos.

Si las secciones son no circulares, la cinta sobrestima el área de la sección (y por tanto el
diámetro).

Basta recordar que para un perímetro dado el círculo es la figura que posee
mayor área. No obstante este sesgo es (en circunstancias normales) muy
pequeño. Cuando en este caso se usan forcípulas, una única lectura de
diámetro por árbol, puede provocar errores (mayores o menores tanto
positivos como negativos en función de que eje se esté midiendo).

En secciones elípticas las forcípulas estiman más exactamente el área de la sección transversal
que la cinta diamétrica, siempre y cuando:

Se midan por árbol los diámetros mayor a y menor b de la elipse, independientemente que
formen o no ángulo recto entre ellos.

π
El área se calcule como g= d1 ⋅ d 2
4
o, lo que es igual, se cante el diámetro medio geométrico d = d1 ⋅ d 2 en vez de lo usual que
d1 + d 2
es cantar el diámetro medio aritmético d=
2

Con estas precauciones la estimación del diámetro es mejor (aunque sin grandes diferencias) con
el uso de forcípula que con el uso de cintas diamétricas.

Sin embargo generalmente las lecturas de forcípulas suelen hacerse de esta manera:
- medición de diámetro máximo y mínimo y calculando media aritmética.
- medición del diámetro máx. y el que forma con él ángulo recto y considerar media aritmética.
- medición de dos diámetros perpendiculares entre si y considerar media aritmética

En estos casos los errores cometidos son mayores que si se mide con cinta diamétrica.

Página 36


PRECISIÓN:

La cinta diamétrica es más precisa que la forcípula. Debido a que su escala está multiplicada por
π existe una mayor separación (tres veces más) entre marcas de medida y es más fácil (en caso
de necesitarse) realizar una medición con mayor exactitud.

FACILIDAD PARA SU CORRECTO USO.

Es necesario asegurarse de mantener la adecuada presión (en el caso de la forcípula) o bien la
adecuada tensión (en el caso de la cinta diamétrica) en el momento de la medición.
En ambos métodos es, asimismo, muy importante asegurarse de que el instrumento de medición,
se coloque perpendicular al eje del árbol.

Posturas inadecuadas inducen a errores que son proporcionales al ángulo I j de desvío respecto a
la posición óptima. "' En el caso de la cinta diamétrica se mediría una elipse de diámetro mayor
n.secfjJy de diámetro menor n.
"En el caso de la forcípula se mediría una elipse de diámetro mayor nl.secfjJ1J7 diámetro menor
n2.secfjJ2 ya que en las dos mediciones podemos cometer este tipo de error.

COMODIDAD:

La cinta diamétrica es más pequeña y ligera, las forcípulas son más pesadas y aparatosas y
producen una mayor fatiga cuando se usan durante largos turnos de trabajo. Las incomodidades
aumentan cuando se trabaja en pendientes acusadas o en montes de difícil transitabilidad.

DETERIORO Y SUS ERRORES INDUCIDOS:

En ambos casos es posible la aparición de errores asociados al deterioro de los distintos
materiales. Las cintas (tanto textiles como de fibra de vidrio) pueden variar en sus dimensiones y
los brazos de la forcípula pueden dañarse y dejar de ser exactamente perpendiculares a la barra
de medición.
Generalmente cintas y forcípulas cuidadosamente mantenidas no producen este tipo de errores.
No obstante y dado que el trabajo en monte no es precisamente un trabajo delicado conviene
realizar una revisión regular de los aparatos, mediante mediciones de comprobación y desechar
aquellos instrumentos deformados por el uso.

USO EN ÁRBOLES EN PIE:

Ambos instrumentos son fáciles de usar en árboles en pie. No obstante cuando se trata de la
medición de diámetros usando escaleras o subiendo al árbol una forcípula puede resultar un
importante estorbo añadido. Además una medición usando cinta es más rápida que dos lecturas
de forcípula (recordemos que para conseguir exactitudes semejantes en árboles no circulares son
necesarias dos mediciones).
Por otra parte evita tener que calcular la lectura media ya sea aritmética o geométrica.

En árboles superiores a 50 cm de diámetro el uso de la cinta diamétrica convencional puede
resultar virtualmente imposible dada la dificultad de abarcar el tronco para realizar su medición.
En los casos en los que el diámetro es superior a 70 cm la mayor parte de las forcípulas tampoco
son efectivas. Para ello conviene contar con cintas diamétricas con algún medio para que
extremo sea fijado al árbol (clavo,…) y permita rodear el árbol para la medición.

Página 37


USO EN ÁRBOLES APEADOS:

Lógicamente es mucho más adecuado en este caso el uso de forcípula que el de cinta,
especialmente si solo es necesaria una medición por sección (caso de elaboración de tablas de
frecuencias o para el cálculo del área basimétrica total apeada en distintos árboles, etc.). En el
estudio de secciones a distintas alturas de árboles individuales conviene realizar dos medidas.

En este caso es desaconsejable el uso de cinta ya que supone rodear la troza o el árbol, y en el
caso de árboles apeados supone pasar la cinta por debajo de los mismos.

PRECIO:

Las cintas diamétricas son sensiblemente más baratas que las forcípulas.

EQUIPO DE MEDICIÓN:

La elección del instrumento de medición depende de las habilidades de los equipos que la van a
realizar. Si son personas acostumbradas al uso de unos determinados aparatos, su mejor
rendimiento y los hábitos correctos pueden compensar por si sola la elección de esos
instrumentos.

TRADICION E HISTORIA:

Muchas veces el uso de uno u otro aparato viene condicionado por la tradición forestal de una
determinada región o país. Los servicios forestales creados a partir de la llamada escuela
alemana y nórdica emplean mucho más la forcípula, mientras que los herederos de las escuelas
francesa e inglesa, con mediciones antiguamente basadas en perímetro normal, se decantan más
por la cinta diamétrica.

Asimismo en lugares con árboles nativos de grandes diámetros (ej. países tropicales) el uso de la
cinta ha sido generalizado.

Página 38


1.6.1. RECOMENDACIONES PARA LA MEDICIÓN DE ALTURAS

La medición de alturas de los árboles se efectuará con mucho cuidado con el fin de evitar
posibles fuentes de error.

• Emplear, preferentemente, aparatos basados en principios trigonométricos (Blume-Leiss,
Suunto o Vertex).
• Emplear aparatos con escalas directas de alturas en lugar de los que miden únicamente
ángulos o pendientes.
• Reconocer el árbol visualmente antes de medir. Reducir así errores de apreciación con
árboles inclinados o por identificación correcta del ápice y/o de la base.
• Para ubicarse a una distancia determinada para el uso de la escala correspondiente en el
aparato de medición, usar preferentemente una cinta métrica sobre el terreno siguiendo
una curva de nivel.
• Desde el punto de medición se deben hacer dos o tres lecturas y obtener luego el
promedio de las mismas. Si la variación entre las lecturas es mayor de 2,5% del valor
promedio, se deberán repetir las mediciones.
• En masas muy densas (repoblaciones o masas no aclaradas) donde habitualmente
existen dificultades para apreciar el ápice del árbol a medir, se puede tratar de mover
ligeramente el tronco apoyándose en él para que la persona que realiza la medición
pueda distinguir su ápice.
• Donde exista mucho matorral que impida ver la base del árbol, colocar un jalón de altura
conocida (o una persona) y a puntar en lugar de a la base al su punto más alto del jalón.
Sumar después la altura del mismo a la medición obtenida.
• La distancia horizontal al árbol deberá ser parecida a su verdadera altura. Como norma
general, habrá que ponerse en el punto desde el que mejor visión de la base y la copa
del árbol se obtenga y si es posible, a un nivel más alto que la base. Siempre que la
visibilidad lo permita:

• 15 m para árboles menores de 18 m (máx altura leída con Blume Leis sobre la
horizontal: 20 m)
horizontal: 30 m)
horizontal: 45 m)
• 40 m para árboles mayores de 40 m (máx. altura leída con Blume Leis sobre la
horizontal: 60 m)

• Cuando se utiliza solo el dióptrio para estacionar a la distancia elegida del árbol y
la visual sobre la mira es inclinada por estar situado en terreno con pendiente, se debe
realizar la siguiente corrección. Se medirá en la escala graduada en ángulos del
hipsómetro la inclinación desde la que se observa la mira y se calculará la corrección a
realizar sabiendo que:
hverdadera = hleida x cos2i Siendo i, la inclinación de la visual.

Justificación:

Al observarse la mira bajo el ángulo i la longitud
interceptada está dividida por el coseno de i. Por otra
parte, como lo que se mide es la distancia oblicua y no la
distancia horizontal nuevamente se está mayorando la
altura por el coseno de i.

Página 68


Forcípula de brazo móvil. Forcípula registradora Masser.

Forcípula finlandesa. Cinta pi.

Calibrador de corteza. Regla de Christen.

Barrena de Pressler. Martillo de sondeo o de Pressler.

Hipsómetro Suunto. Blume-Leiss.

Dióptrio y mira de Pardé.

Página 69


Hipsómetro digital Vertex III.

También se verán los siguientes aparatos:

Tablilla para estadillos y mapas. Forcípula registradora Mantax con Martillo
Kapplan.

Relascopio. Topofil de Chaix

Lupas de precisión. Reflector de espejos.

Brújulas. Altímetro.

Contador. Cinta métrica.

Pentaprisma Telerrelascopio

Página 70

Capitulo del libro "Dendrometría" (2.003) Diéguez, et al. FUCOVASA.

Tabla de Pendientes Distancia sobre el terreno

D i s t a n c i a e n h o r i z o n t a l
TANG GRADOS 8 10 15 20 25 30
0,05 3,0 8,01 10,01 15,02 20,03 25,03 30,04
0,06 3,5 8,01 10,02 15,03 20,04 25,05 30,06
0,07 4,0 8,02 10,02 15,04 20,05 25,06 30,07
0,08 4,5 8,02 10,03 15,05 20,06 25,08 30,09
0,09 5,0 8,03 10,04 15,06 20,08 25,10 30,11
0,10 5,5 8,04 10,05 15,07 20,09 25,12 30,14
0,11 6,0 8,04 10,06 15,08 20,11 25,14 30,17
0,11 6,5 8,05 10,06 15,10 20,13 25,16 30,19
0,12 7,0 8,06 10,08 15,11 20,15 25,19 30,23
0,13 7,5 8,07 10,09 15,13 20,17 25,22 30,26
0,14 8,0 8,08 10,10 15,15 20,20 25,25 30,29
0,15 8,5 8,09 10,11 15,17 20,22 25,28 30,33
0,16 9,0 8,10 10,12 15,19 20,25 25,31 30,37
0,17 9,5 8,11 10,14 15,21 20,28 25,35 30,42
0,18 10,0 8,12 10,15 15,23 20,31 25,39 30,46
0,19 10,5 8,14 10,17 15,26 20,34 25,43 30,51
0,19 11,0 8,15 10,19 15,28 20,37 25,47 30,56
0,20 11,5 8,16 10,20 15,31 20,41 25,51 30,61
0,21 12,0 8,18 10,22 15,34 20,45 25,56 30,67
0,22 12,5 8,19 10,24 15,36 20,49 25,61 30,73
0,23 13,0 8,21 10,26 15,39 20,53 25,66 30,79
0,24 13,5 8,23 10,28 15,43 20,57 25,71 30,85
0,25 14,0 8,24 10,31 15,46 20,61 25,77 30,92
0,26 14,5 8,26 10,33 15,49 20,66 25,82 30,99
0,27 15,0 8,28 10,35 15,53 20,71 25,88 31,06
0,28 15,5 8,30 10,38 15,57 20,75 25,94 31,13
0,29 16,0 8,32 10,40 15,60 20,81 26,01 31,21
0,30 16,5 8,34 10,43 15,64 20,86 26,07 31,29
0,31 17,0 8,37 10,46 15,69 20,91 26,14 31,37
0,32 17,5 8,39 10,49 15,73 20,97 26,21 31,46
0,32 18,0 8,41 10,51 15,77 21,03 26,29 31,54
0,33 18,5 8,44 10,54 15,82 21,09 26,36 31,63
0,34 19,0 8,46 10,58 15,86 21,15 26,44 31,73
0,35 19,5 8,49 10,61 15,91 21,22 26,52 31,83
0,36 20,0 8,51 10,64 15,96 21,28 26,60 31,93
0,37 20,5 8,54 10,68 16,01 21,35 26,69 32,03
0,38 21,0 8,57 10,71 16,07 21,42 26,78 32,13
0,39 21,5 8,60 10,75 16,12 21,50 26,87 32,24
0,40 22,0 8,63 10,79 16,18 21,57 26,96 32,36
0,41 22,5 8,66 10,82 16,24 21,65 27,06 32,47
0,42 23,0 8,69 10,86 16,30 21,73 27,16 32,59
0,43 23,5 8,72 10,90 16,36 21,81 27,26 32,71
0,45 24,0 8,76 10,95 16,42 21,89 27,37 32,84
0,46 24,5 8,79 10,99 16,48 21,98 27,47 32,97
0,47 25,0 8,83 11,03 16,55 22,07 27,58 33,10
0,48 25,5 8,86 11,08 16,62 22,16 27,70 33,24
0,49 26,0 8,90 11,13 16,69 22,25 27,82 33,38
0,50 26,5 8,94 11,17 16,76 22,35 27,94 33,52
0,51 27,0 8,98 11,22 16,83 22,45 28,06 33,67
0,52 27,5 9,02 11,27 16,91 22,55 28,18 33,82
0,53 28,0 9,06 11,33 16,99 22,65 28,31 33,98
0,54 28,5 9,10 11,38 17,07 22,76 28,45 34,14
0,55 29,0 9,15 11,43 17,15 22,87 28,58 34,30
0,57 29,5 9,19 11,49 17,23 22,98 28,72 34,47
0,58 30,0 9,24 11,55 17,32 23,09 28,87 34,64
0,59 30,5 9,28 11,61 17,41 23,21 29,01 34,82
0,60 31,0 9,33 11,67 17,50 23,33 29,17 35,00
0,61 31,5 9,38 11,73 17,59 23,46 29,32 35,18

UNIVERSIDADE DE VIGO - E.U.E.T. FORESTAL DASOMETRÍA E ORDENACIÓN DE MONTES

E.1.1.- Durante el trabajo de campo de un inventario se ha
utilizado un hipsómetro que solo ofrecía lecturas en la
escala de 15 m. Para compensarlo se han medido otros
datos. Se pide calcular la altura del árbol en cada caso.

1. La lectura sobre la banda de 15 ha sido de 20 m.
(suma de las dos lecturas). Con la cinta métrica se han
medido 37 m. sobre el terreno sin pendiente
apreciable.

2. La lectura sobre la banda de 15 ha sido de 26 m. y con la cinta métrica se han medido 41 m.
con una pendiente del 12%

3. La lectura sobre la banda de 15 ha sido de 23 m. En este caso era imposible medir la
distancia con cinta métrica. En lugar de ello se hizo una lectura de la altura del operario que
medía el diámetro. Esta lectura fue de 1,5 m. Al finalizar la parcela se midió la altura del
operario que resultó ser 1,8 m.

Solución:

1. Altura leída: hL = 20 m.
Altura real: hR
Distancia = 37 m.
hL hR

hL hR α
tag (α ) = =
15 D
37 * 20
hR = = 49,3m.
15
15
D
2. Pendiente: tag( i ) = 12%. hL h R
tag (α ) = =
15 D
40,7 * 26
hR = = 70,5m.
15
Corrección por el efecto de la pendiente sobre la mira:
(solo cuando es mayor del 4%)
h´ R = h R * cos 2 (i ) = 69,5m.

3. En este caso se calcula primero la distancia usando para ello la altura del operario.

hL h R 1,8 * 15 18 * 23
tag (α ) = = D= = 18m. hR = = 27,6m.
15 D 1,5 15

Dasometría


E.1.2.- Se pretende medir la altura total de un árbol con un clinómetro (eclímetro). Para ello nos
situamos a una distancia de 13 metros en proyección horizontal del mismo y tal que nuestros
ojos están situados entre la base y el ápice de dicho árbol. Se pide:

a) Cuál será su altura si el ángulo de inclinación obtenido en la visual al ápice es de 53º y el de
la visual a la base es de 9º.
b) Si la inclinación del terreno en el sentido en el que nos hemos desplazado, para medir la
altura del árbol es del 21,25% ¿a qué distancia sobre el terreno equivale la distancia en
proyección horizontal de 13 metros?
c) Qué lectura en el ápice nos daría la visual lanzada con un hipsómetro Suunto desde 13
metros si leemos en la escala de los “20”.
A
Solución:
a)
AC=13⋅tag53º=17,25m.
CB=13⋅tag9º=2,06m.

Altura=AB=AC+CB=17,25+2,06=19,31m.
53º
b)
cos(arctag0,2125)=13/(Dterreno) C
Dterreno=13,29m. 9º

c) Relación tipo: hreal=haparente ⋅ (Dreal/Descala). 21,25%
B

13 m.
Lectura en ápice real= AC=17,25=Lecturaaparente⋅ (13/20)
Lecturaaparente=26,54m.

E.1.3.- Se ha medido con un hipsómetro Suunto, situados a 20m., la altura de un árbol 1
obteniéndose en la escala de 20 como lecturas –1,7 y 10,3. Por detrás de este árbol y a otros
20m. más de distancia horizontal, existe otro árbol 2 en el que sin cambiar de escala ni de
posición el operario ha realizado una lectura en el ápice de 16. Se pide:

a) ¿Cuál es la diferencia de altura real de los dos árboles?
b) ¿Cuál hubiera sido la lectura en la base del árbol 2 de haberla tomado?

Solución:
a) Relación tipo: hreal=haparente ⋅ (Dreal/Descala).
Lectura en ápice real (árbol 2)=16⋅ (40/20)=32m.
En terreno llano la diferencia de alturas será igual que la diferencia de lecturas del ápice.
Diferencia de alturas= Lectura en ápice real (árbol 2) - Lectura en ápice real (árbol 1)=32-10,3=21,7m.

b) En terreno llano ambos árboles tendrán la misma altura basal por lo que:
Lecturareal=Lecturaaparente ⋅ (Dreal/Descala)
1,7= Lecturaaparente ⋅ (40/20)
Lecturaaparente = 0,85

Dasometría


E1.4.- Un camión cuya caja tiene unas dimensiones de 8 m. de longitud y 2,5 m. de anchura,
transporta una carga de 800 apeas. A la entrada en fábrica su peso en báscula es de 40 Tm. y a
su salida en vacio da una tara de 10 Tm. El espacio de la caja del camión se ha aprovechado al
máximo, formando una pila de 2,8 m. de altura.

Se ha estimado el coeficiente de apilado (Ca) mediante la plantilla de Bitterlich (muestreo
angular) por una de las caras de la pila obteniendo los conteos N1=15, N2=17, N3=19 y N4=19.

NOTA: En el muestreo angular con la plantilla de Bitterlich para la estimación de Ca es necesario
aplicar un factor de proporcionalidad de 4, es decir que el conteo de un punto de muestreo debe
multiplicarse por 4 para obtener Ca.

a) ¿Cuál es el peso del estéreo de madera de la pila del camión en Kgs.?
b) ¿Cuál es el volumen real de madera que transporta el camión?
c) Considerando el volumen real el estimado en el apartado anterior ¿Cuál es el diámetro
medio de las piezas?
d) Si el porcentaje de humedad de la madera de la pila es del 21% ¿Cuál es el peso seco de la
madera que transporta el camión?

E.1.5.- El precio de un estéreo de Eucalyptus globulus descortezado es de 20 €. Se sabe que:
El coeficiente de apilado de esa madera es de 0.72
La densidad de la madera en la pila es de 1.21 ton/m3
La corteza supone un 15% en volumen
Se pide:

a) Calcular el precio equivalente de la tonelada sin corteza.
b) Calcular el precio equivalente del metro cúbico con corteza.
c) Calcular cuántos viajes de camión son necesarios para transportar 140 estéreos si el peso
máximo admitido por viaje es de 30 toneladas.

Dasometría


FACTORES DE CONVERSIÓN ENTRE MEDIDAS
Valores medios más usuales

Pinus pinaster Ait.
VOLUMEN VOLUMEN PESO PESO AL ESTÉREO ESTÉREO
3 3
m c.c. m s.c. VERDE (kg) 12% (kg) c.c. s.c.
3
1 m c.c. 1 0,75 1.100-1.200 460 1,5-1,7 -
3
1 m s.c. 1,33 1 1.160-1.250 530-550 2 1,5
1 Tm. 0,9-1,6 0,8-1,5 1.000 1.000 1,4-2,5 1,2-2,0
Estéreo c.c. 0,6 0,45-0,50 700 400 1 0,8
Estéreo s.c. - 0,7 800 500 1,2 1

Eucalyptus globulus Labill.
VOLUMEN VOLUMEN PESO PESO AL ESTÉREO ESTÉREO
3 3
m c.c. m s.c. VERDE (kg) 12% (kg) c.c. s.c.
3
1 m c.c. 1 0,85 1.200-1.400 670 1,5 -
3
1 m s.c. 1,18 1 1.230-1.450 740-830 1,7 1,5
1 Tm. 0,78-1,1 0,8-1,0 1.000 1.000 1,3-1,7 1,2-1,5
Estéreo c.c. 0,64 0,59 770 600 1 0,9
Estéreo s.c. - 0,66 820 660 1,1 1

Otras especies.
PESO AL ESTÉREO
12% (kg) c.c. (kg)
3
Quercus robur 1 m c.c. 670-760 850
3
Betula sp. 1 m c.c. 640-670 -
3
Pinus sylvestris 1 m c.c. 500-540 690
3
Fagus sylvatica 1 m c.c. 690-750 865

Dasometría


OBSERVATORIO DE PRECIOS DE LA MADERA FEARMAGA
Federación Empresarial de Aserraderos y Rematantes de Maderas de Galicia

1. MADERA EN BRUTO PARA SIERRA (EUROS/TM C.C.)

PINO SIERRA CARGADERO
14 a 19 cm para Sierra 20 a 29 cm para Sierra > 30 cm para Sierra

45,00 53,92 57,69

PINO SIERRA EN FÁBRICA

48,83 57,84 61,06

RADIATA SIERRA CARGADERO


45,00 54,93 57,07

RADIATA SIERRA EN FÁBRICA

20 a 29 cm para Sierra > 30 cm para Sierra

57,25 59,66

CASTAÑO SIERRA CARGADERO
> 20 para Sierra

58,88

ACACIA NEGRA SIERRA ACACIA NEGRA SIERRA EN
CARGADERO FÁBRICA
> 20 para Sierra > 20 para Sierra

122,25 125,25

ALISO SIERRA CARGADERO ALISO SIERRA EN FÁBRICA
> 20 para Sierra > 20 para Sierra

44,00 44,94

ROBLE SIERRA EN FÁBRICA
> 30 cm para Sierra

42,00

Dasometría


EUCALIPTO SIERRA CARGADERO EUCALIPTO SIERRA EN FÁBRICA
> 35 cm para sierra > 35 cm para sierra

37,45 51,21

2. MADERAS PARA ASTILLAR(EUROS/TM C.C.)

EN CARGADERO
PINASTER RADIATA EUCALIPTO
30,70 30,70 31,04

EN FABRICA
COSTERO EN FABRICA
PINO EUCALIPTO
38,38 35,2 30,00

3. MADERAS PARA CHAPA Y DESENRROLLO (EUROS/Tm c.c.)

PINO PARA CHAPA PINO PARA DESENROLLO
CARGADERO FABRICA CARGADERO FABRICA
151,25 158,11 75,14 84,14

4. PRODUCTOS ACABADOS

Productos acabados en PINO (precios en Euros/m.c.)
Tabla y tablón de PINO

ENCOFRADO CORRIENTE SEMILIMPIA TABLA 2,5 M

128,79 148,61 206,98 155,67

2500x150 2500x200 2500x300 LIMPIA 30-40 CUADRADILLO
2,500x30x30
150,00 142,00 157,00 334,35 140,00

Productos acabados en EUCALIPTO (precios en Euros/m.c.)

PUNTON 2500x100x35 CUADRADILLO MANGOS
160,00 180,7 210,35

Dasometría



CAPÍTULO 2. CUBICACIÓN POR TROZAS

2. CUBICACIÓN POR TROZAS

Página 106


2. CUBICACIÓN POR TROZAS


Generalmente para la cubicación de la madera se calcula la suma del volumen de cada una de las
trozas que componen el árbol. Para ello distintos autores han asemejado las trozas a distintas
formas geométricas, y han desarrollado distintas fórmulas de cálculo de volumen. A continuación
se muestran las más usadas.

Por ejemplo, la fórmula de Huber, (denominada frecuentemente volumen comercial) se origina a
partir de suponer el volumen de la troza equivalente al de un cilindro cuya sección sea la sección
media de la troza.

Si suponemos que la curva de S es convexa como es probable que ocurra en la primera troza y
en el extremo superior del árbol.

Página 107


Se puede ver que Smalian da el área del trapecio superior, sobrestimando el volumen real.
Huber da el área del trapecio inferior, produciendo una subestimación. Comparando las áreas
entre las líneas de puntos a cada lado de la curva se ve que Huber se acerca mas al valor real.

S1/2

La formula de Huber es generalmente mas exacta y requiere medir un diámetro en lugar de dos.
En muchos casos sin embargo, el centro de la troza no es fácilmente accesible como cuando las
trozas se encuentran apiladas.

Además si se necesita el volumen sin corteza es mas fácil medir los diámetros bajo la corteza en
las extremidades de la troza. Por esto la formula de Smalian, aunque produce errores mayores
tiende a usarse con mayor frecuencia.

Si se tuvieran los tres diámetros, en los extremos y en el centro una media ponderada de Huber
y Smalian reduciría los errores. Se demuestra que la siguiente formula que se puede ver como
una tal media ponderada da resultados exactos para polinomios de hasta tercer grado. Es decir
es exacta para todos los sólidos de revolución aquí considerados. En Dasometría esta se conoce
tradicionalmente como la formula de Newton aunque en matemáticas esta es la base de la regla
de Simpson

S + 4 S 1/ + S
V = 0 2 1
L
6

Es poco usada en la practica excepto en la cubicación de arboles completos.

Página 108



Los defectos en las trozas pueden reducir de manera importante la cantidad de producto que un
aserradero puede obtener. El porcentaje de esta reducción puede ser importante a la hora de
transformar el volumen de madera en rollo a volumen de producto que se puede obtener.

No hay reglas estándar para determinar las pérdidas debidas a los diferentes defectos que las
trozas pueden presentar. No obstante las fórmulas establecidas por Grosenbaugh1 en 1952, y
que se muestran a continuación, son de las más utilizadas y extendidas.

nota: sed =diámetro en punta delgada

Caso 1: Defecto interior

Caso 2: Flecha mayor de 5 cm

M

Caso 3: Extremo desviado del eje

Caso 4: Defecto que afecta a toda la sección

Caso 5: Defecto que afecta a un sector de la sección

1
Grosenbaugh, L.R. 1952. Shortcuts for cruisers and scalers. US Forest Service, Southern Forest Expt. Sta. Occas. Paper
126. p 24.

Página 109


EXIGENCIAS TECNOLÓGICAS DE LA ROLLA DE PINO
CHAPA
CARÁCTER DESENROLLO SIERRA ASTILLA APEAS ESTACAS
PLANA
Longitud
----- ----- 2.50 2.00 5.50 1.50
(m.) troza
Curvatura mínima mínima mínima ----- mínima baja
<0.5 <1
Conicidad <1 cm/m <1 cm/m ----- -----
cm/m cm/m
Diám menor
35 30 12 4 6 6
(cm. s. c.)
Eje centrado centrado ----- ----- ----- -----
Fibra recta recta recta ----- ----- -----
sin nudos, a no ser
Nudos sin nudos ----- ----- ----- -----
cilindro central

Fuente: “Manual de Selvicultura del Pino Radiata” 1999. Proyecto Columella. ADAPT. http://www.agrobyte.com

Página 110



Las reglas madereras son tablas o formulas que dan el volumen aserrado en función del diámetro
menor y el largo de la troza. Se han obtenido a través de diagramas o como formulas derivadas
con razonamientos geométricos.

En el método de diagramas se dibujaron a escala cırculos de varios tamaños representando el
extremo menor de las trozas. En estos se marcaron las tablas que se obtendrıan en el aserrado y
se calculó su volumen.

COSTEROS

La regla maderera de este tipo más conocida es la de Scribner (1846).

Una ligera variante la Scribner decimal C, es una de las mas usadas actualmente en los E.E.U.U.

Entre las reglas de formula una de las mas exactas es la Internacional debida a Clark en 1906,
que dispone lo siguiente:

Primero: se considera que a cada tabla de 1 ”de espesor corresponde un corte donde se pierde
1/8 en serrín y se necesita 1/16 ”de tolerancia por contracción. Es decir, se aprovecha 1 ” en 19
/16 ”, de modo que el área πd2 /4 del extremo menor se reduce multiplicándola por 16
/19.Luego se resta el área que se perderá en cantos y costeros. Ésta tiene una forma irregular
pero se aproxima a un anillo exterior con una profundidad independiente del diámetro.

Página 111


De otra forma, puede estimarse que de cada tabla cortada se pierde en los bordes
aproximadamente la misma cantidad. En todo caso, este término que se resta es proporcional a
D con una constante estimada experimentalmente.

Para un largo de 4 ’ se multiplican estos dos términos por el largo para obtener el volumen
recuperable, que en unidades Board Foot2 y para diámetro en pulgadas es

Esta formula se puede modificar para anchos de corte distintos de 1/8”, y la más usada es la de
1/4”. Con este corte el área del círculo debería haberse reducido por un factor de 16/21 en lugar
de 16/19, por lo que simplemente es necesario ajustar la fórmula obtenida multiplicándola por
19/21,obteniéndose:

A diferencia de la regla de Scribner, la Internacional tiene en cuenta la conicidad. Supone que se
aprovechan tablas de 4’ de largo y que la conicidad media para ese largo es de ½”. La fórmula
anterior se aplica entonces a partir del extremo menor a cada tramo de 4’ incrementando el
diámetro en ½” para el tramo siguiente.

En su aplicación comercial estas reglas madereras van acompañadas por una serie de normas
detalladas para la toma de mediciones redondeo de cifras y deducciones por defectos.
Especialmente en masas extramaduras, los defectos (pudrición fendas, trozas torcidas) suelen ser
importantes. La idea general se basa en encerrar el defecto en un paralelepípedo pensando en la
forma como se harían los cortes y descontar su volumen antes de aplicar la regla.

Las reglas madereras tradicionales solo pueden dar una estimación generalizada ya que la
conversión varía mucho con la tecnología del aserradero especie, dimensiones de los productos
etc. Para una situación determinada es posible desarrollar una regla maderera empírica o función
de conversión a través de estudios de aserrado. Se mide un cierto número de trozas cubriendo el
rango de diámetros deseado, se procesan y se mide la madera obtenida. Con estos datos se
puede entonces ajustar una ecuación de regresión dando el volumen aserrado en función del
diámetro menor y posiblemente del largo si este varía.

2
Board Foot, (pie maderero) unidad de medida de madera para aserrío muy utilizada en EEUU, que es el volumen de
una pieza cuadrada de 1 pie por lado y una pulgada de espesor.

Página 112



CAPÍTULO 3. CUBICACIÓN DE TRONCOS COMPLETOS

3.1. MÉTODO DE CUBICACIÓN DE MEYER.

3.2. TIPOS DENDROMÉTRICOS
3.2.1. Tipos dendrométricos y Curvas de Perfil


3.4. COEFICIENTES MÓRFICOS

3.5. FÓRMULAS APROXIMADAS

3.6. TARIFAS Y TABLAS DE CUBICACIÓN
3.6.2. Tarifas para Inventario Forestal de Galicia (1986)

3.7 EJERCICIOS

Página 113


3. CUBICACIÓN DE TRONCOS COMPLETOS

3.1. MÉTODO DE CUBICACIÓN DE MEYER.

Este método también denominado método planimétrico se basa en representar el
árbol mediante un gráfico que enfrenta la alturas distintos puntos del árbol con el área de
las secciones que el árbol tiene en esos puntos. El área encerrada bajo esa curva es
equivalente al volumen del árbol.

Cubicación de Meyer

160
Alturas de las distintas secciones (dm)

140

120

100
Areas de las
secciones
(dm2) 80

60

Volumen del Árbol (dm3)
40

20

0

-2 3 8 13 18 23

X2 X1 Alturas a las que se encuentran las distintas
Área de las secciones (dm2)
secciones (dm)

La superficie puede planimetrarse con papel milimetrado, un planímetro o programas de
CAD. Los errores más comunes al emplear este método son los relacionados con las
escalas de los ejes y la unidades de volumen en las que viene expresado el resultado.

La localización de los puntos de medición puede realizarse de forma objetiva (por
ejemplo cada 1 m independientemente de deformaciones puntuales) o subjetiva (para
evitar medir diámetros anormales, engrosamientos puntuales, inserciones de ramas,
etc.).

Esta estimación se usa frecuentemente como referencia en la comparación de oitras
mediciones que eremos más adelante. No obstante, el gran número de mediciones que
hacen falta hace que resulte un método caro.

Página 114


3.2. TIPOS DENDROMÉTRICOS

3.2.1. Tipos dendrométricos y Curvas de Perfil

El tronco de un árbol se puede asimilar, para simplificar el cálculo de su volumen, a un cuerpo
geométrico perfecto. En función de las especies y del modo de crecimiento (espesura) la forma
del árbol se puede considerar muy próxima al cono, cilindro, paraboloide, etc...

Los tipos dendrométricos de la consideración de asimilar los troncos a un cuerpo sólido
engendrado por la revolución producida por una generatriz, una curva plana al girar alrededor de
un eje (el eje del árbol).

A la generatriz se le denomina curva de perfil y tiene por ecuación general:

D2 = k ⋅ xn
En la página siguiente se muestran los tipos más habituales (cono cilindro, paraboloide,
neiloide...) y las fórmulas para el cálculo de sus volúmenes

Es indudable que la forma de un árbol está relacionada con el desarrollo de la copa. Si la altura
de la copa es pequeña con relación a la altura del árbol, se tendrá árboles de forma muy regular
(cilindro, paraboloide). Por el contrario, si la copa está muy desarrollada como en los árboles
aislados, se tendrán formas de fuste tendiendo hacia el cono.

En general:

• a la forma cilíndrica se asemejan aquellos árboles de fuste corto, por lo general, fustales de
frondosas en masas densas.

• al paraboloide se aproximan los pies de masas regulares de resinosas (por ejemplo;
coníferas que crecen en masa regular P. Sylvestris).

• la forma cónica es típica de árboles que pertenecen a masas claras, tanto de coníferas como
de frondosas. También las resinosas en latizal.
• El neiloide es propio de árboles aislados, árboles tropicales.

• En el caso general son valores mayores de n mayores que 3 los que aportan un mejor ajuste
al árbol completo.

Si se quiere cubicar un árbol como si se tratase de un sólido perfecto se cometen errores graves
debido a que en ningún caso el árbol se ajusta en su forma a un sólido perfecto y, sobre todo, a
que es difícil tomar los valores de diámetro en punta delgada y altura del fuste.

La mejor aproximación a la forma real del árbol, se hace descomponiendo éste en trozas y
aplicando a cada una de ellas el tipo geométrico más apropiado. Así, por lo general, la parte
inferior del árbol se ajusta a un neiloide, el tramo medio inferior a un cilindro o a un paraboloide,
el tramo medio superior a un paraboloide y el extremo superior a un cono o a un paraboloide. No
obstante los puntos de inflexión entre estas formas no presentan un patrón definido.

Página 115


Según los distintos valores que toma n se generan los distintos tipos dendrométricos que son los
siguientes.
CILINDRO PARABOLOIDE

CONO NEILOIDE

Fórmulas de los Volúmenes de los tipos dendrométricos

π
CILINDRO v= D 2h v = S0 ⋅ h
4

π S 0⋅h
PARABOLOIDE v= D 2h v=
8 2

π
TRONCO DE PARABOLOIDE v= ( D 2 + d 2 )h
8

π S 0⋅h
CONO v= D2h v=
12 3

π
TRONCO DE CONO v= ( D 2 + Dd + d 2 )h
12

π S 0⋅h
NEILOIDE v= D2h v=
16 4

d 2 + D 2 + 3 d 4 * D 2 + 3 d 2 * D4
TRONCO DE NEILOIDE v= π ∗h
16

S0⋅h
TIPO DENDROMÉTRICO D = k ⋅ x v=
2 n
n
D , diámetro en la base
d, diámetro en punta delgada
Donde:
h, longitud de la troza o tronco completo
So, sección basal

Página 116


Comparación de árbol real con modelizaciones para su cubicación. El Eucalipto "El Abuelo" es
el árbol de mayor diámetro del rodal de Chavín (Viveiro - Lugo). En este rodal existen eucaliptos
que aunque con menor diámetro que este, llegan a superar los 70 m de altura.

Nube de puntos altura-diámetro para Pinus radiata
300 puntos procedentes de 100 ejemplares en los alrededores de Canberra (Australia)

Tendencia a Neiloide
( Diámetro relativo 2 )

Tendencia a Cono Tendencia a Paraboloide

( 1 - altura relativa )
Adaptado de Crook 1998

Página 117



Las funciones de perfil se desarrollan con el fin de predecir el diámetro en cualquier punto del
tronco de un árbol.

En general se buscan modelos que devuelvan la curva de perfil de un árbol, de una determinada
especie y localización, con solo introducir los valores de diámetro normal y altura total.

El ajuste de este tipo de ecuaciones se lleva realizando desde hace bastante tiempo, pero ha sido
la potencia de cálculo de los ordenadores la que ha permitido el ajuste de complejas ecuaciones
polinomiales.

Generalmente el tronco se divide en distintas partes y se buscan ajustes por separado.

Pese a la variedad de ecuaciones utilizadas este método hay que ser muy cautos en la
generalización de sus resultados ya que adolece de las siguientes debilidades:

• Pueden existir errores localizados en distintas partes del árbol pese a que el
ajuste del total sea bueno.

• Existe una gran variabilidad entre los distintos árboles de una misma masa
(Incluso en los caos de selvicultura clonal, la posición relativa de los árboles en la
masa puede condicionar de gran manera el perfil del árbol)

Para ilustrar el primer aspecto, en la página siguiente, se muestra el caso de un ajuste de una
ecuación polinomial realizado para 300 pares de datos de Pinus radiata.

A primera vista el ajuste es muy bueno, explica el 98% de la variación y el error promedio en
todo el árbol es próximo a cero. No obstante existen errores localizados en la base (subestimado
en 1 cm) y en la porción del árbol entre le 10% y el 40% de la altura (1cm sobrestimado). Estos
errores se compensan con otros que aparecen más arriba en al árbol, pero si consideramos que
la mayor parte del volumen de un árbol y, sobre todo las trozas de mayor valor, tienden a ser las
de el tercio inferior del árbol, estos errores locales son muy importantes.

A continuación se presenta un ejemplo de un ajuste de distintas ecuaciones polinomiales para
distintos tramos de los fustes de Pinus pinaster en Albacete (Tolosana y Prieto 1991).

El objetivo de esta investigación era definir el perfil de forma que pudiera permitir, no solo la
cubicación, sino también la clasificación de la madera resultante, para los distintos usos.

Página 118


Página 119


Función de perfil de P. pinaster (Albacete) para cubicación de
árboles en pie con clasificación de productos.
Según A.Prieto y E. Tolosana Comunicaiones INIA Serie Recursos Naturales nº 58 - 1991
1,2

1

0,8

0,6

0,4

0,2

0
2

4

6

8
0

5

1
04

08

12

16

24

28

32

36

44

48

52

56

64

68

72

76

84

88

92

98
0,

0,

0,

0,

95
0,

0,

0,

0,

0,

0,

0,

0,

0,

0,

0,

0,

0,

0,

0,

0,

0,

0,

0,

0,
0,
Proporción de la altura total

Ecuaciones de las funciones de Perfil para cubicación de

P. pinaster (Albacete) en pie con clasificación de Productos
(tomado de A. Prieto y E. Tolosana 1991)

Tramo 1 0 ≤ x ≤ 0,1 Y = 0,28527 ⋅ X
Tramo 2 0,1 ≤ x ≤ 0,2 Y = 0,02853 + 0,66314 ⋅ ( X − 0,1) + 0,00034 ⋅ ( X − 0,1) 3
Tramo 3 0,2 ≤ x ≤ 0,4 Y = 0,09484+ 0,89036⋅ ( X − 0,2) + 0,00010⋅ ( X − 0,2)2 + 0,00270⋅ ( X − 0,2)3
Tramo 4 0,4 ≤ x ≤ 0,6 Y = 0,27290 + 0,61799 ⋅ ( X − 0,4) − 0,00152 ⋅ ( X − 0,4) 2 + 0,05638 ⋅ ( X − 0,4)3
Tramo 5 0,6 ≤ x ≤ 0,8 Y = 0,39688 + 0,73588 ⋅ ( X − 0,6) + 0,03231 ⋅ ( X − 0,6) 2 + 0,00738 ⋅ ( X − 0,6) 3
Tramo 6 0,8 ≤ x ≤ 0,85 Y = 0,54529 + 1,15548 ⋅ ( X − 0,8) + 0,02788 ⋅ ( X − 0,8) 2 − 0,04544 ⋅ ( X − 0,8) 3
Tramo 7 0,85 ≤ x ≤ 0,9 Y = 0,60313 + 1,92343 ⋅ ( X − 0,85) + 0,02106 ⋅ ( X − 0,85)2 − 0,07481⋅ ( X − 0,85)3
Tramo 8 0,9 ≤ x ≤ 0,95 Y = 0,69934 + 2,60218⋅ ( X − 0,9) + 0,00984⋅ ( X − 0,9)2 − 0,05485⋅ ( X − 0,9)3
Tramo 9 0,95 ≤ x ≤ 0,975 Y = 0,82947 + 1,98893 ⋅ ( X − 0,95) + 0,00161 ⋅ ( X − 0,95) 2 − 0,02147 ⋅ ( X − 0,95)3
Tramo 10 0,975 ≤ x ≤ 1 Y = 0,87920 + 4,83214 ⋅ ( X − 0,975) + 0,00000002 ⋅ ( X − 0,975) 2 − 0,000000006⋅ ( X − 0,975)3

Página 120


LECTURA AVANZADA

Si consideramos la fórmula D = k ⋅ x Los paraboloides pueden ser divididos en paraboloides
2 n

cuadráticos y cúbicos. Un paraboloide cuadrático (n=1) generará una línea recta si se representa
la altura frente al radio al cuadrado, mientras que un paraboloide cúbico (n=0,66) generaría una
línea recta si representáramos la altura frente al radio al cubo.

Metzger propuso que la forma del tronco de un árbol debería ser próxima a un paraboloide
cúbico. Considera que el tronco era un pilar de resistencia uniforme a la flexión anclada
(empotrada) por la base al suelo y que funcionaría como un brazo de palanca. Una fuerza
horizontal en dicho pilar ejercería un esfuerzo que se incrementaría hacia la base, (punto de
empotramiento) y que la forma más económica de un pilar para resistir dicho esfuerzo sería la de
una silueta uniforme similar a un paraboloide cúbico truncado.

Gray (1956) (citado en Carron 1968) admitía que el árbol no está firmemente empotrado al
suelo. Entonces un paraboloide cuadrático sería más adecuado a las solicitaciones mecánicas que
sufriría el árbol.

Las teorías mecánicas acerca de la forma del tronco son una forma de aproximarse al problema
de la explicación y cálculo de la forma del árbol. No obstante existen otras dos escuelas
científicas con aproximaciones distintas.

Una de ellas considera la necesidad que tiene el árbol para el transporte a su través de agua y
nutrientes y trabaja con ideas basadas en el movimiento de líquidos a través de conductos y
capilares.

Una última aproximación es la llamada teoría hormonal concibe que las hormonas y substancias
que controlan el crecimiento del árbol, son originadas en las hojas y traslocadas desde la copa
para controlar la actividad del cambium. Estas substancias reducirían o favorecerían el
crecimiento radial en puntos específicos del tronco y, por tanto afectarían a la forma del mismo.

Página 121


Página 122



1 - Según Meyer el área bajo la curva de
secciones en función de la altura da el
volumen de una troza.
2.- d(x) es el diámetro de una sección del
árbol que depende lógicamente de l a
altura a la que es medido.
3.- Si el árbol se asimila a un tipo
dendrométrico entonces d(x)=y e y2=p—Xn

π π π
x1 x1 x1

Vg = ∫ 4 [d ( x)] dx = ∫ 4 y dx = ∫4 p ⋅ x n dx =
2 2

x2 x2 x2

π π
] π
( )
x1

x n+1
p x1 p n +1 n +1
= ∫ p ⋅ x dx = n
= x2 − x1
4 x2 4 n +1 x2 4 n +1

S 1/2
Volumen comercial de una troza

Lo calcularemos por la fórmula
de Huber.
x2
L/2
x1
L = x1 - x2

π
Vc = S1/ 2 ⋅ L = S1/ 2 ⋅ ( x1 − x2 ) = d 1 / 2 ⋅ ( x1 − x2 ) =
2

4
π π x1 + x2 n
= p ⋅ x1 / 2 ⋅ ( x1 − x2 ) = p⋅( ) ⋅ ( x1 − x2 )
n

4 4 2

Página 123


Comparación entre Vg y Vc
π
x1 + x2 n x + x2 n
p ⋅(
) ⋅ ( x1 − x2 ) ( 1 ) ⋅ ( x1 − x2 )
Vc 4 2 2
= = =
Vg π p n +1 n +1 1 n +1 n +1
⋅ ( x1 − x2 ) ⋅ ( x1 − x2 )
4 n +1 n +1
n +1
n + 1 ( x1 + x2 ) n ⋅ ( x1 − x2 ) n + 1 ( x1 + x2 ) n ⋅ ( x1 − x2 ) x1
= n n +1 n +1
= n n +1 n +1 n +1
=
2 ( x1 − x2 ) 2 ( x1 − x2 ) x1

 x2  n + 1 (1 + λ ) n ⋅ (1 − λ )
= cambio variable λ =  = n
 x1  2 (1 − λn +1 )

en el caso del fuste completo x2 = 0 y λ = 0 entonces :

Vc n + 1 n +1
= n es decir Vc = n
Vg
Vg 2 2

Página 124


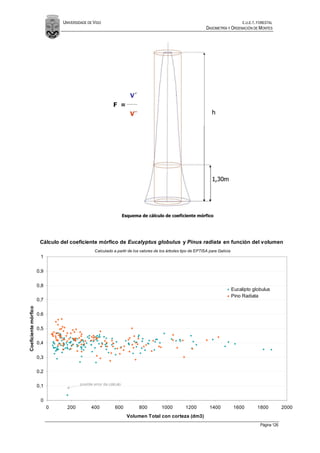
3.4. COEFICIENTES MÓRFICOS

El coeficiente mórfico (también llamado factor de forma) es una manera de resumir el conjunto
de los aspectos de la forma de un árbol en relación a su volumen

Mediante este factor el volumen del árbol es calculado en comparación con e volumen de un
sólido de referencia del mismo diámetro en la base y con su misma altura total.

Generalmente cuando se habla de coeficiente mórfico se sobreentiende que la forma geométrica
de comparación es un cilindro que tenga como diámetro, el diámetro normal del árbol (Diámetro
a la altura del pecho = diámetro a 1,30 m).[Fórmula de König]

Según esto el coeficiente mórfico se calculará como la razón entre el volumen del árbol y el
volumen del cilindro de referencia, es decir:

V
f =
π
⋅ d ⋅ h
2
n
4

Por ejemplo, para los tipos dendrométricos estudiados, el coeficiente mórfico sería:

Neiloide f = 0.25

Cono f = 0,33

Paraboloide cuadrático f = 0,50

Paraboloide cúbico f = 0,60

Cilindro f = 1,00

Otros ejemplos para distintos casos son:

• Árboles de fuste corto, fustales de frondosas en masas densas (f ≈ 0,90).

• Pies de masas regulares de resinosas (por ejemplo; coníferas que crecen en masa
regular P. sylvestris); f ≈ 0,7.

• Árboles que pertenecen a masas claras, tanto de coníferas como de frondosas o
resinosas en latizal. f ≈ 0,50.

• Árboles aislados f ≈ 0,35.

Entonces, si conocemos, o podemos calcular de forma fiable, el coeficiente mórfico de un árbol
de una especie, edad y localización determinada, entonces el volumen se calcularía únicamente
multiplicándolo por la sección normal y la altura.

π 
= f ⋅  ⋅ d ⋅ hi 
2
V i ni
 4 
Página 125


Esquema de cálculo de coeficiente mórfico

Cálculo del coeficiente mórfico de Eucalyptus globulus y Pinus radiata en función del volumen
Calculado a partir de los valores de los árboles tipo de EPTISA para Galicia
1

0,9

0,8
Eucalipto globulus
Pino Radiata
0,7
Coeficiente mórfico

0,6

0,5

0,4

0,3

0,2

0,1 posible error de cálculo

0
0 200 400 600 800 1000 1200 1400 1600 1800 2000
Volumen Total con corteza (dm3)
Página 126


Cociente de forma (Form quotient)

Es el cociente entre el diámetro en a alguna altura estandarizada h (generalmente por
encima de la sección normal) y el diámetro normal.
d
Es decir: q = h

d n

Es, como en el caso anterior una forma de simplificar y resumir la forma del fuste.

Se han utilizado distintos criterios (tanto absolutos como relativos) para el establecimiento de la
altura de referencia, como por ejemplo:

- a 4 metros (absoluto)

- a la mitad de la altura entre la sección normal y la punta del árbol (relativo)

En este último caso por ejemplo podemos relacionar los valores obtenidos con la asimilación de
la forma del árbol a un determinado tipo dendromético según los siguientes valores.

- 0.325 - 0.375 (clase 35) neiloide

- 0.475 - 0.525 (clase 50) conoide

- 0.675 - 0.725 (clase 70) paraboloide cuadrático

- 0.775 - 0.825 (clase 80) paraboloide cúbico

Página 127


.

Cociente de forma en Pino Radiata (Galicia)

1

0,9

0,8
D a 4m / D normal

0,7

0,6

0,5

0,4
0 50 100 150 200 250 300 350 400 450 500
Diámetro normal

Coeficiente de forma para una muestra de Pino radiata en Galicia

1,2

1

0,8
D a 4m / Dn

0,6

y = -0,7609x + 0,9802
R2 = 0,4244
0,4

0,2

0
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7
4 m / Altura total

Página 128


3.5. FÓRMULAS APROXIMADAS

Fórmula de Pressler:

Este método de cubicación original y sagaz fue presentado hace más e 125 años por el ilustre
forestal alemán Pressler.

Ya se ha visto que, de alguna manera, el tronco de un árbol puede asimilarse según los casos a
un cono un paraboloide o un neiloide. Si S es la sección de la base y h la altura los volúmenes
se calculan como:
PARABOLOIDE CONO NEILOIDE
S ⋅h S ⋅h S ⋅h
v= v= v=
2 3 4
Si en cada caso buscamos a que altura se encuentra el diámetro igual a la mitad del diámetro de
la base, esta sería:
3 1
h1 = h h1 = h h1 = 0,37 ⋅ h
4 2
4 100
h= h1 h = 2 ⋅ h1 h = ⋅ h1
3 37
Si sustituimos h en las fórmulas de los volúmenes obtenemos aproximadamente la misma
fórmula
S 4 2 2 ⋅h 100 S ⋅ h1 100 2 ⋅h
v= h1 = ⋅ S ⋅ h1 v= 1
v= = S ⋅ h1 ≈ 1
23 3 3 37 4 148 3

Es decir independientemente de la forma del árbol

2
V = S ⋅ ⋅ h1
3

Página 129


Esta fórmula de cubicación quedó mucho tiempo sin utilización práctica debido a la dificultad de
medir h1 conocida como "altura del punto normal o altura de Pressler" .

No obstante la aparición del relascopio de Bitterlich eliminó esta dificultad y recuperó la fórmula
del olvido. Actualmente los modernos dendrómetros también permiten sencillamente el cálculo de
esta altura.

Las deformaciones de la base de los árboles tienen un efecto nefasto en la exactitud de esta
fórmula ya que afectan tanto al valor S como al h1.

Por ello para utilizar la fórmula de Pressler se procede de la siguiente manera:

Se calcula mediante la fórmula de Pressler, a partir del valor del diámetro normal, el volumen de
la porción del tronco entre 1,30 m y la altura total.

Posteriormente al valor resultante se le añade el volumen de la troza basal cubicada por alguna
fórmula comercial (Smalian o Huber).

Página 130


Fórmula de König:

Esta fórmula es la abordada al hablar de coeficiente mórfico, el volumen del árbol es calculado
en comparación con el volumen de un cilindro que tiene como diámetro, el diámetro del tronco a
la altura del pecho.

π
V = f ⋅ ⋅d n
2
⋅h
4

Fórmula de Von Cotta:

Es la fórmula análoga a la de König pero utiliza como sólido de referencia un tronco de cono que
tiene como diámetro, el diámetro del tronco a la altura del pecho.

El metro a la real con corteza:

Es el volumen de un cilindro de diámetro igual a la media del diámetro a 1,30 m. del suelo y del
diámetro de sierra (d = 20 cm.) con una altura igual a la altura maderable (en este caso, hasta
diámetro en punta delgada de 20 cm.)

1 π 
V = — (d + 0,2) 2 hs
4 4 

donde: d, diámetro normal con corteza (m.)
hs, altura maderable, hasta 20cm. de diámetro de fuste.

El metro a a la cuarta o a la cuarta sin deducción:

Es el volumen de un prisma cuadrado de lado igual a un cuarto de la circunferencia media entre
la circunferencia a 1,30 m. del suelo y de la circunferencia de diámetro mínimo maderable (d=20
cm. -> c ≈ 60 cm.) y de una altura igual a la altura maderable (hs).

 dπ + 0,2π 
2 2
 d + 0,2 
V =  h s = π 2hs  
 8   8 

Este es el sistema que usan habitualmente los compradores de madera en pie en el País Vasco.
Su justificación está en la compensación por las pérdidas debidas a la corteza (aproximadamente
un 10%) y por las pérdidas debidas al costero.

Página 131


3.6. TARIFAS Y TABLAS DE CUBICACIÓN


Las tarifas de cubicación son expresiones matemáticas que proporcionan el volumen de
una masa bien a partir de la consideración de árboles individuales (Tarifas de cubicación de
árboles individuales) o considerando la masa como un conjunto continuo de individuos (Tarifas
de cubicación de masas).

En la cubicación de madera que se va a destinar a su comercialización las tarifas que se
emplean normalmente son las de árboles individuales, que proporcionan el volumen de madera a
partir de la medición de determinados parámetros en el árbol, que a efectos de utilización de la
tarifa se denominan entradas. Hay varios tipos de tarifas de cubicación de árboles individuales:

- Tarifas de cubicación de árboles individuales de una entrada:

Proporcionan el volumen de un árbol en función del diámetro normal.

Su expresión matemática tiene la forma: V = f {D n }

donde V puede ser cualquier tipo de volumen (volumen total, comercial, etc.) y Dn es el
diámetro normal del árbol considerado.

- Tarifas de cubicación de árboles individuales de dos entradas:

Suministran el volumen de un árbol en función de dos parámetros, generalmente del
diámetro normal (Dn) y de la altura total (Ht) del árbol.

Su expresión matemática tiene la forma: {
V = f Dn ,H t }
Algunas veces se sustituye la altura total por la altura maderable o del fuste (Hf, altura
hasta un determinado diámetro en punta delgada, generalmente 7 o l0cm con
corteza), aunque este procedimiento es menos utilizado que el anterior por la dificultad
que presenta la determinación de este tipo de altura.

- Tarifas de cubicación de árboles individuales de tres entradas:

Proporcionan el volumen de un árbol en función del diámetro normal, de una altura,
generalmente la altura total, y de otro parámetro x que puede ser muy diverso
(cualquier altura, diámetro, espesor de la corteza, etc.).

Su expresión matemática es la siguiente: {
V = f Dn ,H t , x }

Página 132


En general, la precisión de la estimación del volumen dado por una tarifa de cubicación
aumenta cuando aumenta el número de entradas, pero de una manera cada vez menor, es decir
la diferencia en precisión entre una tarifa de una entrada y una de dos entradas es mayor que la
que existe entre una tarifa de tres entradas y una de dos. Por ello se establece como límite el uso
de tarifas de tres entradas, ya que el empleo de tarifas con mayor número de entradas no
supondría una gran diferencia en cuanto a la precisión en la cubicación, y por el contrario se
aumentarían mucho los costes de medición.

Cualquier tarifa de cubicación, para que su aplicación sea correcta, debe ir acompañada
siempre, como mínimo, de la siguiente información:

- especie para la que la tarifa es aplicable,

- zona de validez geográfica,

- definición de la variable dependiente

(salida de la tabla, volumen que proporciona, unidades de medida).

- definición de las variables independientes (entradas) y unidades de medida.

Además de estos cuatro puntos es interesante conocer:

- el número de árboles muestra que se han utilizado para la construcción de la tarifa,

- el ámbito geográfico en el que se han tomado los árboles muestra,

- el procedimiento de determinación de los volúmenes de los árboles muestra,

- el método de construcción de la tarifa y modelos utilizados,

- el autor y la fecha de publicación de la tarifa.

En el caso de que se quiera utilizar para la cubicación de un rodal una tarifa de la misma
especie pero construida para una zona geográfica diferente o en el caso de que se quiera usar
una tarifa de carácter general (ámbito geográfico grande que incluye la zona donde se encuentra
el rodal que se quiere medir), se deben comparar los volúmenes de una muestra de árboles de la
masa donde se quiere emplear la tarifa con los volúmenes de los mismos árboles cubicados con
esa tarifa.

Las tarifas de cubicación tienen como principal ventaja su mayor precisión en comparación
con las tablas de cubicación y además permiten informatizar el cálculo del volumen en una
sencilla hoja de cálculo.

Las tarifas de cubicación más empleadas en Galicia son:

- las obtenidas en el "Estudio para la obtención de fórmulas de cubicación y crecimientos
por pies de cuatro especies maderables para el inventario forestal de Galicia (Pinus

Página 133


pinaster, Pinus radiata, Pinus sylvestris y Eucalyptus globulus) " (Xunta de Galicia,
1.986),

- las elaboradas en el Segundo Inventario Forestal Nacional para Galicia (ICONA, 1993).

3.6.2. Tarifas para Inventario forestal de Galicia (1986)

En el primer trabajo "Estudio para la obtención de fórmulas de cubicación y crecimientos por
pies de cuatro especies maderables para el inventario forestal de Galicia" (Xunta de Galicia,
1.986) se obtuvieron tarifas de dos y de tres entradas, de ámbito autonómico, para las siguientes
especies:

- Pinus pinaster, - Pinus sylvestris

- Pinus radiata, - Eucalyptus globulus.

Y para las siguientes variables de salida:

- volumen total con corteza, - volumen del fuste con corteza

- volumen total sin corteza, - volumen del fuste sin corteza

Para Pinus pinaster se obtuvieron dos series de tarifas, una para masas procedentes de
regeneración natural, denominada Serie N, y otra para las masas procedentes de repoblación,
denominada Serie R.

Estas tarifas se obtuvieron a partir de mediciones en árboles apeados, troceados y
medidos de las cuatro especies en diferentes puntos de Galicia siendo el total de árboles medidos
de 561. Las tarifas polinómicas de dos entradas, en función de la altura total y el diámetro
normal, obtenidas para las especies que abarca el presente estudio son las que se presentan en
el cuadro siguiente.

Página 134


Eucalyptus globulus

Volumen total con corteza − 44,09 + 0,21 ⋅ 10 −4 ⋅ h ⋅ Dn + 0,35 ⋅ 10 −2 ⋅ h ⋅ Dn
2

Volumen de fuste con corteza − 56,08 + 0,21 ⋅ 10 −4 ⋅ h ⋅ Dn + 0,36 ⋅ 10 −2 ⋅ h ⋅ Dn
2

Volumen total sin corteza − 52,25 + 0,17 ⋅ 10 −4 ⋅ h ⋅ Dn + 0,34 ⋅ 10 −2 ⋅ h ⋅ Dn
2

Volumen de fuste sin corteza − 62,13 + 0,17 ⋅ 10 −4 ⋅ h ⋅ Dn + 0,34 ⋅ 10 −2 ⋅ h ⋅ Dn
2

Pinus radiata

Volumen total con corteza 28,95 + 0,28 ⋅ 10 −4 ⋅ h ⋅ Dn
2

Volumen de fuste con corteza 20,70 + 0,28 ⋅ 10 −4 ⋅ h ⋅ Dn
2

Volumen total sin corteza − 89,96 + 0,22 ⋅ 10 −4 ⋅ h ⋅ Dn + h
2

Volumen de fuste sin corteza − 86,29 + 0,22 ⋅ 10 −4 ⋅ h ⋅ Dn + 9,12 ⋅ h
2

Pinus pinaster (Serie N)

Volumen total con corteza 20,01 + 0,30 ⋅ 10 −4 ⋅ h ⋅ D n
2

Volumen de fuste con corteza 13,84 + 0,30 ⋅ 10 −4 ⋅ h ⋅ Dn
2

Volumen total sin corteza 7,63 + 0,23 ⋅ 10 −4 ⋅ h ⋅ Dn
2

Volumen de fuste sin corteza 2,69 + 0,23 ⋅ 10 −4 ⋅ h ⋅ Dn
2

Pinus pinaster (Serie R)
Volumen total
6,11 + 0,32 ⋅ 10 −4 ⋅ h ⋅ Dn
2
con corteza
Volumen de
fuste con 0,07 + 0,32 ⋅ 10 −4 ⋅ h ⋅ Dn
2

corteza
Volumen total
sin corteza
− 1,03 + 0,78 ⋅ 10 −4 ⋅ h ⋅ Dn − 0,12 ⋅ 10 −2 ⋅ h ⋅ Dn + 0,7 ⋅ 10 −2 ⋅ Dn
2 2 2

Volumen de
fuste sin − 6,74 + 0,79 ⋅ 10 −4 ⋅ h ⋅ Dn − 0,12 ⋅ 10 −2 ⋅ h ⋅ Dn + 0,72 ⋅ 10 −2 ⋅ Dn
2 2 2

corteza

Página 135



Las tarifas de cubicación construidas para el Segundo Inventario Forestal Nacional
(ICONA, 1993) son tarifas de dos y tres entradas que permiten calcular volumen maderable con y
sin corteza y también volumen de leñas gruesas, en función de tres factores característicos como
son: especie, calidad, situación geográfica y forma de cubicación. Para cada provincia gallega se
obtuvieron tarifas para las especies forestales que se indican en los siguientes cuadros:

II IFN

Página 136



Las tablas de cubicación no son más que la representación en cuadros numéricos de los
valores de volumen obtenidos al aplicar una tarifa de cubicación para unos valores determinados
de los parámetros que hay que medir en el árbol. Por tanto, igual que las tarifas, existen tablas
de cubicación de una, dos o tres entradas, aunque normalmente se emplean las tablas de
cubicación de dos entradas. Estos dos parámetros de entrada a la tabla son generalmente el
diámetro normal y la altura total, y como salida se obtiene el volumen del árbol.

Al igual que para la aplicación de las tarifas de cubicación, para un correcto empleo de la
tabla de cubicación es necesario conocer especie para la construyó, la tarifa que dio origen a la
tabla, su zona de validez geográfica, definición de la salida que da la tabla, es decir, tipo de
volumen que proporciona y unidades de medida, y definición de las entradas y unidades de
medida de éstas.

El empleo de tablas de cubicación en lugar de tarifas tiene como ventaja su mayor
facilidad de manejo que permite el cálculo de volumen de un árbol de forma inmediata y sin
hacer cálculos, por lo que son muy prácticas a la hora de cubicar pequeños lotes de madera en el
mismo monte.

Las tablas de cubicación con más difusión en Galicia son:

- Tabla de cubicación para Pinus pinaster de los Servicios Forestales de la Xunta de
Galicia.

- Tabla de cubicación para Eucalyptus globulus de los Servicios Forestales de la Xunta
de Galicia.

- Tabla de cubicación para Pinus pinaster de los antiguos Distritos del Servicio
Forestal (1.940-1.960)

- Tabla de cubicación para Pinus radiata de los antiguos Distritos del Servicio Forestal
(1.940-1.960)

- Tabla de cubicación para Eucalyptus globulus, zona norte, de los antiguos Distritos
del Servicio Forestal (Pita -1.967)

Respecto a la utilización de estas tablas, es preciso señalar que no existe para muchas de
ellas referencia sobre algunos de los aspectos que se consideran fundamentales para que su
aplicación sea correcta, como son la tarifa a partir de la que se construyeron, la zona de validez
geográfica, volumen que proporciona y unidades de medida, el número de árboles muestra que
se utilizaron para la construcción de la tarifa que la originó, el autor y la fecha de publicación de
la tarifa a partir de la cual se construyó la tabla, etc.

Página 137


E.3.7.- Se apea un pino de 23,5 cm. de diámetro normal,
dejando en el suelo un tocón de 25,3 cm. de diámetro y
30 cm. de altura. El tronco de 11,5 m. de longitud total se
corta en trozas hasta de un diámetro en punta delgada
de 10 cm. con corteza. Las longitudes de las trozas y las
medidas hechas en sus secciones medianas: diámetros
con corteza, espesor de la corteza e incrementos
radiales de los últimos 10 años, figuran en la tabla
adjunta. Se pide calcular:

1. Los volúmenes de las trozas y de los fustes
maderables con y sin corteza.

2. El volúmen del fuste maderable con corteza, por la fórmula de cubicación comercial y por la
fórmula de Smalian.

3. Representar la forma del fuste maderable hace 10 años y en el momento actual con y sin
corteza.

4. El porcentaje de corteza del fuste maderable.

5. El volúmen de la troza de sierra hasta punta delgada de 20 cm. c.c.

6. El volúmen de la troza anterior utilizando la fórmula de Newton.

7. El coeficiente mórfico del fuste con y sin corteza.

8. El coeficiente mórfico del tronco con y sin corteza.

9. El crecimiento medio anual.

10. El crecimiento corriente anual (media de 10 años).

Monte: Valle del Conde (Burgos)
Especie: 26 Edad: 45
Altura del fuste: 98 dm. Altura total: 115 dm.
Diámetro normal c.c.: 235 mm. Espesor de corteza: 25 mm.
Diámetro tocón c.c.: 253 mm. Diámetro punta delgada 10 mm.

DIAMETRO ESPESOR DE CRECIMIENTO LONGITUD
CENTRAL (mm) CORTEZA (mm) (mm) TROZA (dm)
235 25 15 20 40 anillos anuales
215 17 16 20
185 15 17 20
160 8 20 20
135 4 22 15

Página 146


E3.8.- Con la intención de hacer una cubicación por trozas se han tomado los datos de diámetros
y alturas de las diferentes secciones de un eucalipto apeado en Boiro (A Coruña). La altura del
fuste hasta punta delgada de 10,45 cm. es de 17,9 m.

18
Monte: Riobo.
Concello: Boiro
Provincia: A Coruña.
Especie: Eucalyptus globulus.
16
Diámetro normal: 52,5 cm.
Altura total: 25,2 m.
Altura fuste: 17,9 m.
Altura tocón: 0,3 m.
14

Longitud (m) Diám. cc (cm) en
Troza
desde el tocón el centro
0 60,75
12
1 0,5 58,00
2 1,5 52,50
3 2,5 49,00
10 4 3,5 45,10
5 4,5 41,10
6 5,5 39,60
7 6,5 36,00
8 8 7,5 34,80
9 8,5 29,00
10 9,5 28,80
11 10,5 28,70
6
12 11,5 23,00
13 12,5 20,00
14 13,5 18,20
15 14,5 16,00
4
16 15,5 12,30
Punta delgada: 10,45

2
1) Calcular el volumen del fuste apeado por trozas usando las
fórmulas de Smalian y por Huber.

2) Representar el gráfico de Meyer.
0
- 0,4 - 0,2 0 0,2 0,4

3) Representar la altura relativa [(h-hi)/h] frente a la sección relativa
[Pi/4*(di/hi)2] y calcular la curva que mejor se ajusta al perfil del
árbol.

4) Integrar esta curva para calcular la función del volumen. Usar esta función para determinar el
volumen de la troza que va desde 8,5 m. hasta 12 m. de altura.

Página 147


E.3.9.-

Se apea un pino de 30 años y de 43 cm. de diámetro normal, dejando en el suelo un tocón de
47,5 cm. de diámetro y 15 cm. de altura. El tronco de 19 m. de altura total se corta en trozas
hasta un diámetro en punta delgada de 7,5 cm. con corteza. En la tabla se adjuntan los valores
de las longitudes de las trozas y las medidas hechas en sus secciones mediana y extremas de
diámetro con corteza y espesores radiales de corteza.

Altura de la Longitud de la Diámetro Espesor de
Troza
sección (m) troza (m) (cm) corteza (mm)
0,15 47,5 25
1 1,15 2 43,8 22
2,15 40,0 21
2 3,15 2 35,5 19
4,15 31,0 18
3 5,15 2 26,8 17
6,15 22,5 15
4 7,15 2 18,8 13
8,15 15,0 12
5 9,15 2 14,1 11
10,15 13,2 10
6 11,15 2 12,9 8
12,15 12,5 8
7 13,15 2 10,0 7
14,15 7,5 7
Raberón 19,00 4,85

1) Cuál es la altura del fuste.
2) Los volúmenes de las trozas con y sin corteza utilizando las fórmulas de Huber, Smalian y
Newton. Obtener a partir de dichos valores el volumen maderable y total del árbol.
3) El volumen del fuste maderable c.c. por las fórmulas de Huber, Smalian y Newton.
4) Los volúmenes del fuste maderable con y sin corteza por el método gráfico de Meyer.
5) El porcentaje de corteza del fuste maderable.
6) El volumen de la troza de sierra hasta punta delgada de 20 cm. c.c. utilizando el gráfico de
Meyer.

30

20

10

0

-10 0 2 4 6 8 10 12 14 16 18 20
-20

-30

Página 148

E.U.E.T. FORESTAL
Solución ejercicio 3.7

1º) Los volúmenes de las trozas y de los fustes maderables con y sin corteza.

DIAM Corteza DIAM LONG Sección Huber Huber
dcc mm mm dsc mm m m2 vol m3cc vol m3sc
235 25 185,0 2 0,043 0,0867 0,0538
215 17 181,0 2 0,036 0,0726 0,0515
185 15 155,0 2 0,027 0,0538 0,0377
160 8 144,0 2 0,020 0,0402 0,0326
135 4 127,0 1,5 0,014 0,0215 0,0190
Suma: 0,2748 0,1945

2º) El volúmen del fuste maderable con corteza, por la fórmula de cubicación comercial y por la fórmula de Smalian.

HUBER:
DIAM Corteza DIAM LONG Dist tocón Inc. Diam.
dcc mm mm dsc mm m m mm/m
215 17 181,0 2 3 15
185 15 155,0 2 5

Diámetro 1/2 (4.75 m) = 188,75 Vcc m3 = 0,266

SMALIAN:
DIAM LONG Sección
dcc mm m m
253 9,5 0,050
100 0,008 Vcc m3 = 0,276

3º) Representar la forma del fuste maderable hace 10 años y en el momento actual con y sin corteza.

DIAM Corteza DIAM Altura Crecimiento Diam sc -10 Sección cc Sección sc Secc sc -10
dcc mm mm dsc mm m mm mm m2 m2 m2
253 0,3 0,050
235 25 185,0 1,3 15 155 0,043 0,027 0,019
215 17 181,0 3,3 16 149 0,036 0,026 0,017
185 15 155,0 5,3 17 121 0,027 0,019 0,011
160 8 144,0 7,3 20 104 0,020 0,016 0,008
135 4 127,0 9,1 22 83 0,014 0,013 0,005

Forma del Fuste Maderable Gráfico de Meyer

10 10
9 9 Edad 45 cc
8 8 Edad 45 sc
7 7
Alturas (m)
Alturas (m)

Edad 35 sc
6 6
5 5
i
4 4
3 3
Edad 45 cc
2 2
Edad 45 sc
1 1
0 Edad 35 sc 0
0 50 100 150 200 250 300 0,00 0,01 0,02 0,03 0,04 0,05 0,06
Diámetros (mm) Sección (m2)

4º) El porcentaje de corteza del fuste maderable.

Huber Huber
vol m3cc vol m3sc
0,0867 0,0538
0,0726 0,0515
0,0538 0,0377
0,0402 0,0326
0,0215 0,0190
0,2748 0,1945 % Corteza= 29,21

Prácticas de Dasometría

E.U.E.T. FORESTAL
5º) El volúmen de la troza de sierra hasta punta delgada de 20 cm. c.c.

HUBER:
DIAM Corteza DIAM DIAM Dist tocón Inc. Diam.
dcc mm mm dsc mm dcc mm m mm/m
235 25 185,0 235 1 10
215 17 181,0 215 3 15
185 15 155,0 185 5

Long troza comercial (punta de 20) = 4 m Vcc m3 = 0,115
Diámetro 1/2 (a 2 m) = 225 mm

SMALIAN:
DIAM Long Sección
dcc mm m m2
253 0 0,050
200 4 0,031 Vcc m3 = 0,163

6º) El volúmen de la troza anterior utilizando la fórmula de Newton.

Newton
DIAM Long Sección
dcc mm m m2
253 0 0,050
225 2 0,040
200 4 0,031 Vcc m3 = 0,160

7º) El coeficiente mórfico del fuste con y sin corteza.

Volúmen del cilindro Volúmen del fuste
m3 cc m3 sc m3 cc m3 sc
0,412 0,255 0,275 0,195
(aparentes)
fcc= 0,667
fsc= 0,762

8º) El coeficiente mórfico del tronco con y sin corteza.

9º) El crecimiento medio anual.

im (volumen)= Volumen/edad

Altura DIAM 45 DIAM 35 LONG Huber 45 años Huber 35 a.
m dsc mm dsc mm m vol m3sc vol m3sc

1,3 185,0 155 2 0,0538 0,0377
3,3 181,0 149 2 0,0515 0,0349
5,3 155,0 121 2 0,0377 0,0230
7,3 144,0 104 2 0,0326 0,0170
9,2 127,0 83 1,5 0,0190 0,0081
0,1945 0,1207

im (vol) 45 años= 4,32 dm3 sc/año
im (vol) 35 años= 3,45 dm3 sc/año

10º) El crecimiento corriente anual.

ic (volumen)= Volumen 45 - Volumen 35 / (45-35) = 7,38 dm3 sc/año

Prácticas de Dasometría

Solución ejercicio 1.3. Cubicación comercial por trozas.
3
Nº de troza Longitud (m) Diám. cc (cm) Superficie Vol. (dm ) Vol. (dm3) Nº de troza Altura sobre x y (cm2/m2) x2 y2
2
de Huber desde el tocón en el centro (dm ) Huber Smalian de Smalian h=17,9 el tocón (hi) (h-hi)/h Pi/4 * di2/h2
0 60,75 28,99 - 0,00 1,0000 9,0464 1,000 81,838
1 0,5 58,00 26,42 132,1 69,3 1 0,25 0,9860 8,2459 0,972 67,995
2 1,5 52,50 21,65 216,5 180,3 2 1,00 0,9441 6,7562 0,891 45,646
3 2,5 49,00 18,86 188,6 202,5 3 2,00 0,8883 5,8854 0,789 34,638
4 3,5 45,10 15,98 159,8 174,2 4 3,00 0,8324 4,9858 0,693 24,858
5 4,5 41,10 13,27 132,7 146,2 5 4,00 0,7765 4,1406 0,603 17,145
6 5,5 39,60 12,32 123,2 127,9 6 5,00 0,7207 3,8439 0,519 14,776
7 6,5 36,00 10,18 101,8 112,5 7 6,00 0,6648 3,1768 0,442 10,092
8 7,5 34,80 9,51 95,1 98,5 8 7,00 0,6089 2,9685 0,371 8,812
9 8,5 29,00 6,61 66,1 80,6 9 8,00 0,5531 2,0615 0,306 4,250
10 9,5 28,80 6,51 65,1 65,6 10 9,00 0,4972 2,0331 0,247 4,134
11 10,5 28,70 6,47 64,7 64,9 11 10,00 0,4413 2,0191 0,195 4,077
12 11,5 23,00 4,15 41,5 53,1 12 11,00 0,3855 1,2967 0,149 1,681
13 12,5 20,00 3,14 31,4 36,5 13 12,00 0,3296 0,9805 0,109 0,961
14 13,5 18,20 2,60 26,0 28,7 14 13,00 0,2737 0,8119 0,075 0,659
15 14,5 16,00 2,01 20,1 23,1 15 14,00 0,2179 0,6275 0,047 0,394
16 15,5 12,30 1,19 11,9 16,0 16 15,00 0,1620 0,3708 0,026 0,138
punta delgada 17,9 10,45 0,86 - 29,7 17 17,90 0,0000 0,2677 0,000 0,072
VOLUMEN TOTAL (dm3): 1.476,5 1.509,4
MEDIA 0,5712 3,3066 0,4130 17,8981
VARIANZA 0,0918 7,3743 0,1161 600,2255
1. Calcular el volumen del fuste apeado por trozas usando las fórmulas de Smalian y por Huber. COVAR 0,7291 - 7,1894 -
COEF DE CORR. (x, y) 0,9382 0,9120
3 3
Volumen Total (Smalian): 1.509,4 dm Volumen Total (Huber): 1.476,5 dm

2. Representar el gráfico de Meyer. 3. Representar la altura relativa [(h-hi)/h] frente a la sección relativa [Pi/4*(di/hi)2] y calcular la curva que mejor se ajusta al perfil del árbol.

Curva de perfil del árbol y = 10,927x3 - 6,8875x2 + 4,4303x
Gráfico de Meyer 10 R2 = 0,9894
35
9
30 8
25 7

20 6
5
15
4

y=Pi/4 (di/h)2
10 3
5 2

Área de la sección (dm2)
0 1
0 20 40 60 80 100 120 140 160 0
Altura de la sección (dm) 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
x=(h-hi)/h

4. Integrar esta curva para calcular la función del volumen. Usar esta función para determinar el volumen de la troza que va desde 8,5 m. hasta 12 m. de altura.

Cubicación por la curva de perfil: Cálculo del volumen de la Troza 8,5-12 por la curva de perfil. Longitud (m) x
[Área = Integral de la curva entre h y h´] desde el tocón (h-hi)/h
Vol(h;h´)=-Área*h3*10-4 (mc) Vol(8,5;12)= 0,1874 (=0,32678977*17,9^3*0,0001) 8,5 0,525
12 0,330

H X INTEGRAL DIF VOL
8,5 0,52514 0,524257133
12 0,32961 0,197467367 0,3267898 104,7067

Cálculo del volumen total por la curva de perfil.

Vol(0;15,5)= 1,484 (=2,5868*17,9^3*0,0001)



CAPÍTULO 4. MEDICIÓN DE MADERA APILADA

4.1. INTRODUCCIÓN
4.2. UNIDADES. EL ESTÉREO
4.3. COEFICIENTE DE APILADO.
4.4. COEFICIENTES DE APILADO TEÓRICOS
4.5. CÁLCULO DEL COEFICIENTE DE APILADO.
4.6. CALCULO DEL VOLUMEN APARENTE DE LAS PILAS
4.7. CALCULO DEL VOLUMEN DE MADERA FLEJADA.

Página 153


4. MEDICIÓN DE MADERA APILADA

4.1. Introducción

Los productos de escaso diámetro, longitud estándar y de relativamente poco valor,
como las leñas y los rollizos para desintegración se comercializan frecuentemente de
acuerdo al volumen en pilas. Además los controles de stock en parque de fábrica, o incluso
en cargadero, pueden tenerse que llevar a cabo sobre pilas de madera.

Página 154


4.2. Unidades. El estéreo

El estéreo es la madera contenida en una pila de 1×1×1 metros de volumen (un metro
cúbico apilado, o un metro cúbico aparente).

El estéreo puede referirse a madera apilada con corteza o sin corteza

Otras unidades utilizadas en el mundo son:

metro ruma: utilizada para medición de madera para pasta en Chile. Es el
volumen de madera contenido en una pila de sección 1×1 metros y
con trozas de 2,44 m de largo.

Cord: es la unidad más utilizada en Norteamérica. Es el volumen de
madera contenido en una pila de 4×8 pies con trozas de 4 pies de
largo. Equivale por tanto a 128 pies cúbicos. También denominada
Imperial Cord.

Cunit: Una unidad derivada por la empresa APM (American Paper Mills Pty
Ltd) que al constatar que sus camiones no podían llevar un Cord
(128 pies3) si no que aproximadamente cargaban un volumen
aparente de 100 pies3. Definieron por tanto 1 Cunit = 100 pies3.

Unidad a b c

Estéreo 1m 1m 1m

Metro ruma 1m 1m 2,44 m

Cord 4 pies 8 pies 4 pies

Cunit axbxc = 100 pies3

Página 155


EQUIVALENCIAS ORIENTATIVAS DE UNIDADES DE VOLUMEN APARENTE

CORD CUNIT ESTÉREO METRO CÚBICO BOARD FOOT
Volumen aparente de Volumen sólido de Volumen aparente de Volumen Sólido de Volumen aproximado
128 cubic feet (4´x 4´x 8´) 100 cubic feet 1 m3 (1m x 1m x 1m) 1 m3 1"x12"x12"

1 0,85 3,625 2,407 500
1,176 1 4,264 2,832 600
0,276 0,234 1 0,664 138
0,415 0,353 1,506 1 208
2 1,67 7,25 4,81 1000

Notas:

- Las equivalencias entre volúmenes sólidos y volúmenes aparentes, como es natural, no son fijas, dependen de la conformación de las pilas, de las
características de las maderas apiladas, etc. por tanto estos valores han de tomarse únicamente como valores orientativos.

- El Board Foot, es una medida que pretende describir la madera aserrada que se puede obtener de un conjunto de trozas, por tanto sus equivalencias con
las unidades de volumen sólido y aparente son muy variables en función de parámetros como diámetro de la trozas, su coeficiente mórfico, pese a ello
tradicionalmente se ha fijado la equivalencia entre 5 y 4,53 m3 por cada 1000 BFT

Página 156


4.3. Coeficiente de apilado:

La relación entre volumen aparente y volumen real se denomina coeficiente de
apilado y es siempre menor que la unidad:

volumen real de madera
coeficiente de apilado =
volumen aparente de madera

Al inverso de esta fracción se le suele llamar factor de apilado (estéreos que hacen
falta para obtener un m3 de madera).

El coeficiente de apilado depende fundamentalmente de:

• Longitud de trozas

• Forma e irregularidad de la trozas

• Ramosidad

• Diámetro (medio y varianza)

• El movimiento de la madera cargada en un camión, durante en el
transporte a la fábrica también puede introducir cambios importantes

• Debido a efectos de borde el contenido de madera puede variar con las
dimensiones de la pila

• Pero sobre todo depende de la forma de apilado así que compradores y
vendedores deben establecer normas específicas sobre dimensiones y
métodos de apilado.

Página 157


4.4. Coeficientes de apilado teóricos:

d

d

2 π
Superficiede madera 4 ·d π
C= = 2 = = 0,7853
SuperficieTotal d 4

Este coeficiente se denominó estéreo español (término actualmente en desuso)

d

h
60º

d
1π 2
Superficiede madera 2 4 ·d π d π d
C= = = · = · = 0,906
SuperficieTotal 1
d·h 4 h 4 d·cos30º
2

Página 158


Redes de puntos y muestreo sistemático

Una alternativa mencionada a menudo consiste en tomar fotografías y medir en ellas
la proporción de madera, por ejemplo, con una red de puntos.

Más práctico para uso en terreno sería el método propuesto por Avery. Para ello se
marca una vara a intervalos regulares y se determina la proporción de marcas que caen en
madera al ponerla sobre la cara de la pila. En cualquier caso es necesario hacer un muestreo
lo suficientemente intenso para conseguir la precisión deseada.

Es fácil obtener estimadores insesgados de precisión conocida usando muestreo
aleatorio. El muestreo sistemático, del cual la red de puntos es un caso especial, es
generalmente mucho mas reciente.

Su uso del muestreo sistemático, del cual la red de puntos es un caso particular, es
mucho más reciente y tiene como principales inconvenientes los siguientes:

• la dificultad de estimar la precisión de la estimación. Existen no obstante fórmulas
aproximadas para el cálculo de la varianza en una medición de área con red
cuadrada de puntos se encuentra que es aproximadamente 0,0728 P —A3 donde P es
el perímetro del área a medir y A es el espaciamiento de la red.

• la posibilidad de cometer errores extremos en casos desfavorables. Estos errores
extremos, asociados a coincidencias de periodicidad entre la población y la muestra,
probablemente son raros en la practica, y generalmente pueden prevenirse tomando
precauciones adecuadas.

Una alternativa mencionada a menudo consiste en tomar fotografías y medir en ellas la
proporción de madera con una red de puntos u otro método.

Actualmente la evolución de los tratamientos de imágenes con medios informáticos
permiten la estimación de la cantidad de madera sólida existente en una pila o cargada en la
caja de un camión mediante el uso de escáneres.

Página 160


487.534 / 743.512 = 65,57

18/63 = 0,71

Página 161


Calculo del volumen aparente de las pilas

Página 162


h1 h2 h3 h4

w
d/2 d d d

h1 + h2 + h3 + h4
Volumen aparente = ·w·L
4

Página 163


4.6. Calculo del volumen de madera flejada.

En la madera los costes de manejo (carga, descarga, clasificación, etc...) son muy altos por
m3. Esto ocasiona que en operaciones de transporte de grandes volúmenes de madera a
grandes distancias se necesite alguna manera de simplificar su manejo. Debido a que es un
material poco dado a manejarse en contenedores (salvo en el caso de estar astillado) e
imposible de paletizar, es el flejado en paquetes el sistema más usado, especialmente para
el transporte marítimo.

Lo habitual es que la madera para trituración o desintegración se fleje en paquetes
cilíndricos de tres a cinco toneladas para facilitar su manipulación. Los flejes empleados se
colocan con ayuda de herramientas especiales. En el caso de madera tropical o de calidad,
la dimensión de las trozas hace innecesario este paso, pero en muchas ocasiones (sobre
todo con tropicales) se colocan en las testas de la pieza anillos metálicos para que eviten la
aparición o extensión de fendas durante la travesía y recepción de la madera. En ocasiones,
la colocación de flejes se hace en el mismo puerto mientras se espera la llegada del barco.

En el caso de que la madera se presente flejada o en paquetes, el cálculo de us volumen
apilado será resultado de multiplicar el número de paquetes por el volumen medio (o peso
medio) del paquete.

Para determinar las dimensiones del paquete puede recurrirse por ejemplo a un muestreo

Página 164


CUESTIONES

4.1. ¿Cuántos estéreos son un metro ruma? ¿y una cuerda (cord)?

4.3. Calcula la proporción sólida (factor de apilado) en una pila de cilindros de diámetro
uniforme apilados en forma rectangular. Lo mismo para la disposición más compacta
(triangular).

4.4. En la fotografía siguiente estima la precisión obtenida con la red que se muestra. Haga
una tabla de precisión vs. número de puntos.

Página 165



CAPÍTULO 5. EPIDOMETRÍA

5. INTRODUCCIÓN A LA EPIDOMETRÍA.
5.1. DEFINICIÓN
5.2. ALGUNAS CONSIDERACIONES SOBRE LA ANATOMÍA DE LA MADERA
5.3. MODELOS DE CRECIMIENTO
5.4. METODOLOGÍA


5. Introducción a la Epidometría.

5.1. Definición
La epidometría es la parte de la dasometría que se encarga de medir el crecimiento y desarrollo
en altura de los árboles y masas boscosas desde un punto de vista dinámico. La realización de
estudios epidométricos requiere habitualmente la medición de cada uno de los anillos de
crecimiento. La precisión en la medición de los anillos va en relación con la utilización posterior
de los datos y debe ser máxima en el caso de estudios de dendrocronología.

La medición de los anillos mediante una escala y una lupa binocular es laboriosa suele
descartarse en el caso de realizar gran número de medidas. Se han desarrollado dispositivos
acoplados a ordenadores de modo que las medidas se registran sobre soportes magnéticos. Estos
dispositivos se basan principalmente en una base que se desplaza mientras el observador emplea
una referencia para decidir dónde está situado el límite del anillo. El desplazamiento es registrado
mediante un mecanismo de rotación en los modelos más antiguos como Eklund o bien lineal en
los más modernos como Lintab o Velmex (mesas de posicionamiento lineal). También existen
métodos de análisis de imagen digital para el reconocimiento automático de anillos. Estos
métodos, sin embargo, están restringidos a la madera de coníferas, con anillos fácilmente
reconocibles por la presencia de bandas claras y oscuras; la mayor parte de estos métodos se
encuentran todavía en fase de desarrollo.

5.2. Algunas consideraciones sobre la anatomía de la madera
En la madera de coníferas (pinos, abetos, píceas, etc.) destaca la ausencia de vasos en su
sistema conductor ya que su papel es realizado por las traqueidas. A pesar de ello, presenta
facilidades anatómicas para la medición de los anillos y la mayoría de especies puede ser
preparada simplemente con un corte transversal limpio.

Las especies de frondosas presentan vasos conductores. Segín la distribución de los mismos en
relación al parénquima y al límite del anillo se diferencias especies de poro difuso o de poro en
anillo. Las especies de poro en anillo como las del género Quercus también son sencillas de
preparar y muestran el cambio de anillo con claridad (Figura 1). Los grandes vasos se
corresponden con el inicio del crecimiento en
primavera cuando el árbol sale del período
invernal.

En general, las especies de poro difuso
presentan anillos difíciles de medir porque los
vasos están distribuidos por todo el anillo.
Arces y abedules son especies de poro difuso
que sin embargo pueden medirse fácilmente.
Existen diversos métodos para facilitar la
lectura de los anillos en las especies de este
tipo. La especie Eucalyptus globulus presenta
madera de tipo poro difuso (Figura 2). Por esta
razón es necesario resaltar los cambios que
producen los anillos mediante algún
procedimiento, los más comunes son: lijado o
quemado de la superficie, por reflexión de
distintos tipos de luz y la tinción con colorantes.
Figura 1 .Esquema anatómico del xilema secundario
de las dicotiledoneas. Especie de poro en anillo.


Figura 2. Izq.: Madera de conífera, Pinus ponderosa. Dercha. arriba: Madera de poro en anillo: Quercus rubra.
Dercha. abajo: madera de poro difuso: Acer saccharum.

5.3. Modelos de crecimiento
Los modelos de crecimiento de las masas forestales son una representación simplificada de la
dinámica de las masas o del árbol individual, que tiene en cuenta diversos aspectos tales como el
crecimiento, la mortalidad, la composición y la estructura de la masa. Los modelos de crecimiento
desempeñan un papel clave en la planificación forestal. Esto es así porque permiten predecir el
desarrollo y la evolución de la masa mediante el conocimiento de la diferentes variables que la
caracterizan (VANCLAY, 1994).

Para la elaboración de un modelo pueden usarse tres diferentes enfoques para el muestreo o
sistema de recogida de datos:

Medición de parcelas temporales: se trata de medir parcelas que no se van a volver a medir en
sucesivos inventarios. Ofrecen un a mínima información y por eso no se suelen usar de forma
independiente en la construcción de modelos.

Medición de parcelas permanentes: Como su nombre indica son parcelas que se miden de forma
periódica cada cierto tiempo. Constituyen la mejor y principal fuente de datos para la elaboración
de modelos de producción y crecimiento. Sin embargo son el método más costoso en tiempo y en
recursos.

Análisis de troncos: se trata de medir directamente el grosor de los anillos de crecimiento a
diferentes alturas del tronco y por tanto es fácil conocer la dinámica de crecimiento de los
árboles. El principio de esta técnica es que el árbol se asemeja a un sólido de revolución y las
medidas extraídas a varios niveles permiten reconstruir el perfil del árbol en épocas sucesivas
(PARDÉ, 1994).

Dentro de los estudios y modelos forestales, la calidad de una estación forestal para una
determinada especie se define como la capacidad que potencialmente tiene dicha estación para


producir madera. Aunque su determinación se puede abordar mediante la medición de
parámetros tales como el clima, la litología, la morfología, la edafología, etc. la práctica más
general es hacerlo a través de los atributos de la propia masa forestal que se desarrolla en la
estación. Aunque parecería lógico estimar la calidad de estación o capacidad productiva mediante
el volumen en pie de la masa, numerosos autores (ORTEGA et al., 1988; DAVIS & JOHNSON, 1987)
apuntan que la bondad de la altura como indicador de la calidad radica en el hecho de que
siendo de fácil medida está fuertemente correlacionada con el crecimiento en volumen a la vez
que está poco influida por la densidad y la espesura. Por esta razón los modelos o curvas de
calidad de estación reflejan la evolución de la altura con la edad.

Figura 3. Crecimiento de una masa forestal.

5.4. Metodología
Los estudios epidométricos pueden realizarse a partir de muestras seleccionadas en el aparato de
parcelas de un inventario diseñado con otros objetivos o bien puede diseñarse una recogida de
muestras específica para un estudio determinado. En ambos casos es muy importante la elección
de un número suficiente de árboles y con representatividad adecuada.

En cada individuo loa anillos pueden examinarse mediante una muestra extraída con la barrena
de Pressler o de una manera más exacta mediante el apeo y tronzado del árbol. Se realizan
trozas de un metro de longitud extrayendo una rodaja de unos 5 cm de cada testa para la toma
de datos. Una vez en el laboratorio las muestras son sometidas a diferentes procesos para
resaltar los anillos y facilitar su lectura. Es común que baste con una limpieza pero en ocasiones
es necesario que sean lijadas y teñidas. Para resaltar los cambios de anillos se utiliza
phloroglucinol, un colorante selectivo que tiñe de rojo la lignina dejando la celulosa sin teñir
(PATTERSON AE., 1961). Las muestras son bañadas en una solución de 1 gr. de phloroglucinol en
100 cc. de etanol al 95% durante aproximadamente 1 min. El exceso de colorante se quita con
ácido clorhídrico al 50%.

Las mediciones se realizan sobre el radio o los radios medios de cada sección (Fig. 3). Para ello
sobre cada muestra se miden los radios máximo y mínimo y se localiza el radio o los radios que
desde la médula presenten la longitud media entre ambos. Sobre este radio o radios se miden los
espesores de los anillos. El último anillo de cada sección representa el diámetro (sin corteza) a las
diferentes alturas de cada sección en la edad actual del árbol. El espesor del último anillo de cada
sección representa el crecimiento logrado en el último año y así hacia atrás se puede representar
el crecimiento a lo largo de la vida del árbol.


D3
H3 S3

D2
H2 S2

D1
H1 S1
Figura 3. El análisis de troncos consiste en la
medición en diferentes secciones del árbol (S1, S2... )
distribuidas a los largo del fuste (H1, H2... ) del espesor
de los anillos. Esto permite reconstruir el perfil del
tronco desde el año de su nacimiento hasta el actual y
por lo tanto calcular cualquier parámetro dendromé-
trico del tronco a cualquier edad.

Curva de evolución de la altura. Consiste en la representación de las edades a las que se
alcanzan las alturas de las diferentes secciones muestreadas. La edad a la que el árbol ha
alcanzado la altura de cada sección será la que se obtenga de restar a la edad actual el número
de anillos de dicha sección.

Con la curva de evolución de la altura y una vez detectadas las clases representativas con un
procedimiento estadístico obtenemos la modelización matemática de las curvas de calidad de
estación. Este proceso se realiza a través de una regresión jerárquica multivariante que da como
resultado un haz de curvas de calidad (Fig. 4). Dentro del haz de curvas se suelen fijar un
número de clases discreto, con un intervalo para facilitar la clasificación. En este caso se ha
resumido la variabilidad en 4 clases o intervalos, para nombrarlos suelen usarse números
romanos (I, II, III y IV) o utilizar el llamado índice de sitio (IS) que se define como la altura
alcanzada a los 8 años de edad (Tabla 1). Por último, para ligar la calidad de estación con la
producción real según la Ley de EICHHORN deben respetarse ciertos márgenes en la densidad de
la masa.

HAZ DE CURVAS DE CALIDAD DE ESTACIÓN

30
I
25
II
20 III
ALTURA

15 IV

10

5

0
0 3 6 9 12 15 18

EDAD

Figura 4. Haz de curvas de calidad de estación de E. globulus en A Mariña Lucense según el modelo de
crecimiento de Norte Forestal y la UPM.


CURVA MEDIA Índice de Sitio (m)
CALIDAD I 17,5
CALIDAD II 14,5
CALIDAD III 11,5
CALIDADIV 8,5

Tabla 1. Índice de Sitio. Altura alcanzada por cada calidad media a los 8 años.

Volumen del árbol. El volumen del tronco se calcula por suma de cada una de sus trozas. La
fórmula de cubicación usada es la correspondiente al tronco de cono, que en el caso del eucalipto
da valores muy semejantes a los de SMALIAN. Se calcula así el volumen del fuste sin corteza.

S1 + S 2 + S1S 2
V= H
3

Donde S1 y S2 son las superficies de las caras y H la longitud de la troza.

Crecimiento corriente y medio sin corteza. El crecimiento medio (imv) se calcula como
cociente entre el volumen del fuste y su edad. Para una edad cualquiera i, el crecimiento medio
en volumen será:
vi
imv =
i

El crecimiento corriente (icv) se calcula como cociente entre el incremento en volumen del
intervalo considerado dividido por la duración del intervalo. En este caso puesto que se calcula el
volumen a cada edad el intervalo es de 1 año y por tanto:

vi − vi −1
icv =
1

A continuación se muestran los resultados de un estudio realizado conjuntamente con la
Universidad de Santiago de Compostela (A. Carballeira) sobre eucalipto en Xove para analizar el
crecimiento de cuatro parcelas supuestamente afectadas por contaminación con fluor. Tras la
medición de los anillos de cada una de las secciones para cada parcela se encuentran en la Tabla
2 se presenta un resumen de los resultados. Es la parcela 1 la que muestra peores tasas de
crecimiento enmarcándose en la calidad IV por presentar un Índice de Sitio próximo a 8. La
parcela 3 destaca por presentar un Índice de Sitio que se corresponde con una calidad I.

Cr. corriente Cr. medio Índice de Sitio Número de
Parcela Volumen (m3)
(m3/ha/año) (m3/ha/año) (m) anillos
1 369.5 22.2 13.6 >8 27
2 526.6 35.2 22.9 >11 23
3 638.4 55.9 27.7 >18 23
4 525.2 54.3 23.9 >10 22

Tabla 2. Resumen de los resultados por parcela en el momento de la corta. Índice de Sitio es la altura mínima estimada
para los 8 años según el análisis de troncos.


Figura 5. Curvas de evolución de la altura, el volumen, crecimiento medio y crecimiento corriente para las cuatro parcelas medidas.

1
La evolución de las distintas variables con la edad se encuentra representada en la Figura 5. El
primer gráfico es de evolución de la altura (Calidad de Estación) y puede observarse cómo la
parcela 3 presenta un crecimiento en altura más temprano que el resto de las parcelas. En los
gráficos de evolución del volumen del fuste y del crecimiento medio se observa también cómo la
parcela 3 es ligeramente superior a las demás y la parcela 1 claramente por inferior al resto.

1
Valor calculado para masas puras de Eucalyptus globulus con diámetros a la altura de 1,30 m. mayores de 6 cm. y
densidad estándar.


Todas las parcelas menos la parcela 1 alcanzan los 200 dm3 de volumen de fuste sobre los 15
años, este valor puede suponer unas 220 t/Ha. Valor superior a la media de los montes de
Eucalyptus globulus en Lugo que según el Tercer Inventario Forestal Nacional1 es de 187,9 t/Ha.

CURVAS DE EVOLUCIÓN DE LA ALTURA (m)

P1
30 P3
P4
P2
25 C I-NP2
C II-NP2
C III-NP2
20 C IV-NP2

15

10

5

0
0 5 10 15 20

CURVAS DE EVOLUCIÓN DEL VOLUMEN FUSTE (dm3)

700

600

500

400

300

200

100

0
0 5 10 15 20 25 30

Figura 6. Evolución de la altura y el volumen en las parcelas tipo comparado con las cuatro calidades de estación
tipo de A Mariña Lucense (Modelo Norfor y UPM, 2002)

Del análisis de los datos se desprende que todas las parcelas estudiadas están comprendidas
entre las calidades de estación denominadas tipo de I a IV (Figura 6) por lo que cabe concluir
que no se observan anormalidades en el crecimiento de las parcelas medidas en Xove. Son
destacables las grandes diferencias de producción y calidad entre el máximo y el mínimo
observado en las parcelas, concretamente entre las parcelas 1 y 3, máxime cuando no existe una
gran distancia entre ellas. No obstante de este hecho no pueden deducirse más consideraciones
puesto que sobre el crecimiento influyen un gran número de factores.


EDAD Hpmy Dg G Vm Vsc CMsc CCsc
Pmyha
años m cm m2/ha dm3/pie m3/ha m3/ha/año m3/ha/año
3 9,84 706 9,39 4,89 10,87 7,67 2,55 2,55
4 11,85 799 10,94 7,51 29,89 23,86 5,96 16,19
5 13,56 833 12,21 9,74 49,44 41,17 8,23 17,30
6 15,03 846 13,27 11,70 69,61 58,85 9,81 17,68
7 16,33 849 14,19 13,43 90,14 76,56 10,93 17,70
8 17,50 849 15,00 15,00 110,84 94,08 11,76 17,52
9 18,56 846 15,72 16,43 131,55 111,32 12,37 17,23
10 19,53 843 16,37 17,74 152,16 128,22 12,82 16,89
11 20,42 839 16,97 18,96 172,60 144,74 13,15 16,52
12 21,25 834 17,51 20,09 192,82 160,87 13,40 16,13
13 22,02 830 18,01 21,15 212,78 176,62 13,58 15,75
14 22,74 826 18,48 22,15 232,48 191,99 13,71 15,37
15 23,42 822 18,91 23,09 251,88 207,00 13,80 15,00
16 24,06 818 19,32 23,98 270,99 221,64 13,85 14,64

Tabla 3. Tabla de producción correspondiente a la Calidad I - A Mariña (Modelo de Norfor y UPM, 2002). Altura media
(Hpmy), Número de pies mayores por ha (Pmyha), diámetro medio cuadrático (Dg), área basimétrica (G), volumen unitario
(Vm), volumen de masa (Vsc), crecimiento medio y corriente de volumen sin corteza (CMsc e CCsc).

REFERENCIAS.
ANALISIS DE TRONCOS:
BURROWS, C.J. and Burrow, V.L. 1976. Procedures for the study of snow avalanche chronology
using growth layers of woody plants. Institute of Arctic and Alpine Research, University
Colorado, Boulder, Occasioanl Pape. 23 (39)
COOK, E.R. & KAIRIUKSTIS, L.A. (eds). 1990. "Methods of Dendrochronology. Applications in the
environmental sciences". Kluver. Dordrecht, Boston, London.
DOUGLAS, A.E., 1939. Crossdating in dendrochronology. Journal of Forestry. 39 (825-831)
FRITTS, H.C. 1976. "Tree Rings and Climate". Academic Press, London, UK.
HUGHES, M.K., KELLY, P.M., PILCHER, J.R., LAMARCHE, V.C. 1982. "Climate from tree rings".
Cambridge University Press, Cambridge, London, New York, New Rochelle, Melbourne,
Sydney.
KAENNEL, M. & SCHWEINGRUBER, F.H., 1995. "Multilingual Glossary of Dendrochronology".
Haupt Publishers Berne. Stuttgart. Vienna.
PATTERSON, A.E. 1961. "Distinguishing Annual Rings in Diffuse Porous Tree Species". Journal of
Forestry 59:126.
SCHWEINGRUBER, F.H. 1988. "Tree Rings: Basics and Applications of Dendrochronology". Kluwer
Academic Publishers, Dordrecht, Netherlands.
STOKES, M.A. & T.L. SMILEY. 1968. "An Introduction to Tree-Ring Dating". University of Chicago
Press, Chicago, IL, USA.

MODELIZACIÓN FORESTAL:
ALBORECA, A. (1999). Tablas de producción para los montes españoles. Fundación Conde del
Valle Salazar. Madrid.
ORTEGA ,A. & MONTERO, G. 1988. Evaluación de la calidad de las estaciones. Revista Ecológica
nº 2: 155-184.
VANCLAY, J. (1994) "Modelling forest growth and yield. Application to mixed tropical forest" .
CAB. Wallingford. 312 pp.
PARDÉ, J. & BOUCHON, J. (1994). "Dasometría". Madrid. Mundi-Prensa.
DAVIS L.S. & JOHNSON, K.N. 1987. Forest Management. Third Edition. McGraw-Hill Book
Company.

Cuaderno DASO 2008

Más contenido relacionado

La actualidad más candente

Similar a Cuaderno DASO 2008

Más de Miguel Ángel Cogolludo Agustín

Último

Cuaderno DASO 2008