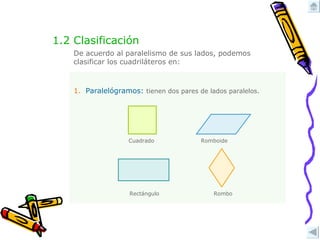
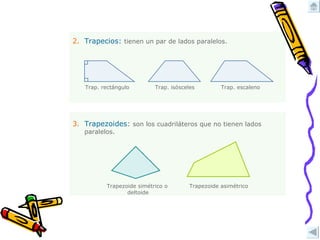
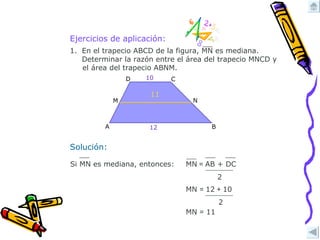
El documento describe las propiedades de los cuadriláteros, incluyendo paralelogramos (cuadrado, rectángulo, rombo, romboide), trapecios (isósceles, rectángulo, escaleno) y trapezoides (simétrico, asimétrico). Explica cómo clasificarlos, calcular sus áreas y perímetros, y aplicar estas propiedades en ejercicios.

1. Cuadriláteros

2. objetivos: Clasificar Cuadriláteros. Identificar las propiedades de los paralelógramos. Aplicar las propiedades de los paralelógramos en la resolución de ejercicios. Identificar las propiedades de cada tipo de trapecio y trapezoide. Aplicar las propiedades de los Cuadriláteros en la resolución de ejercicios.

3. 1. Cuadriláteros 1.1 Definición Además, la suma de sus ángulos interiores es 360°.  : ángulos interiores.  = 360°  ´  ´  ´  ´  : ángulos exteriores.  ´+  ´+  ´+  ´  = 360° A, B, C y D: Vértices del cuadrilátero. Los cuadriláteros son polígonos de cuatro lados, cuatro vértices, cuatro ángulos interiores y cuatro ángulos exteriores. AB, BC, CD y DA: Lados del cuadrilátero.

4. CUADRILÁTEROS PARALELÓGRAMOS TRAPECIOS TRAPEZOIDES Cuadrado Rectángulo Rombo Romboide Trap. Isósceles Trap. Rectángulo Trap. Escaleno Trap. Simétrico o Deltoide Trap. Asimétrico

5. 1.2 Clasificación De acuerdo al paralelismo de sus lados, podemos clasificar los cuadriláteros en: 1. Paralelógramos: tienen dos pares de lados paralelos. Cuadrado Rectángulo Rombo Romboide

6. 2. Trapecios: tienen un par de lados paralelos. Trap. rectángulo Trap. isósceles Trap. escaleno 3. Trapezoides : son los cuadriláteros que no tienen lados paralelos. Trapezoide simétrico o deltoide Trapezoide asimétrico

7. 2. Paralelógramos 2.1 Características generales Lados opuestos paralelos Lados opuestos iguales Ángulos opuestos iguales y ángulos consecutivos suplementarios. Ejemplo: 12 cm 12 cm 6 cm 6 cm AB = DC y AD = BC ABCD, romboide. Las diagonales se dimidian A D C B AB // DC y AD // BC

8. Área = base ∙ altura base = 12 cm h = 4 cm A D C B Ejemplo: Área = 12 ∙ 4 = 48 cm 2

9. 2.2 Cuadrado 4 lados iguales 4 ángulos interiores iguales a 90° Área = (lado) 2 Área = a 2 Perímetro = 4a diagonal = lado ∙ 2 d a a a a d = a 2 Área = d 2 2 Área = (diagonal) 2 2

10. Propiedades de las diagonales: Son iguales: AC = BD Se dimidian: AE = EC = DE = EB Ejercicios de aplicación: 1. Determinar el área de un cuadrado cuya diagonal mide 10 cm. Solución: Como   Son bisectrices Área = (10) 2 2 Área = 50 cm 2 Área = (diagonal) 2 2 Son perpendiculares: AC BD

11. 2. Determinar la diagonal de un cuadrado cuyo lado mide 3 cm. Solución: diagonal = lado ∙ 2 2  diagonal = 3 ∙ 2 2 cm  diagonal = 3 ∙ 2 cm  diagonal = 6 cm

12. 2.3 Rectángulo 2 pares de lados iguales 4 ángulos interiores iguales a 90° (Por teorema de Pitágoras) Área = largo ∙ ancho A = a ∙ b Perímetro = suma de sus 4 lados P = 2(a + b) diagonal(d) = (largo) 2 + (ancho) 2 d = a 2 + b 2

13. Propiedades de las diagonales: Son iguales: AC = BD Se dimidian: AE = EC = DE = EB Ejercicios de aplicación: 1. Determinar diagonal de una rectángulo de lados 5 cm y 12 cm. Solución:     d = 13 cm d = 5 2 + 12 2 diagonal(d) = (largo) 2 + (ancho) 2 d = 25 + 144 d = 169

14. 2. Determinar el perímetro de la zona achurada del rectángulo Por las características de la zona achurada, su perímetro es igual al perímetro del rectángulo. ABCD de la figura. Solución: Luego, el perímetro de la zona achurada es: P = 2( 21 + 12) cm P = 2 · (33) cm P = 66 cm

15. 2.4 Rombo 4 lados iguales ángulos opuestos iguales Área = lado ∙ altura Área = a ∙ h P = 4a Perímetro = suma de sus 4 lados Área = producto de diagonales 2 Área = d 1 ∙ d 2 2

16. Propiedades de las diagonales Son bisectrices. Se dimidian: AE = EC y DE = EB Ejemplo: Son perpendiculares: AC BD

17. 2.5 Romboide 2 pares de lados iguales Ángulos opuestos iguales Área = base ∙ altura P = 2a + 2b Perímetro = suma de sus 4 lados Área = a ∙ h

18. Propiedades de las diagonales Se dimidian: AE = EC y DE = EB

19. 1. Trapecios 1.1 Características Generales M N A B C D Mediana (MN): Trazo que une los puntos medios de los lados NO paralelos. Un par de lados paralelos, llamados bases (AB//DC) MN = AB + DC 2 AB // DC // MN

20. El área del trapecio corresponde a la semisuma de sus bases, por la altura: Área = Mediana ∙ altura ó E C D M N A B h Altura = DE = h La mediana MN, dimidia a la altura h. Área = (AB + DC) ∙ h 2

21. Los ángulos consecutivos de los lados NO paralelos son suplementarios:  

22. TIPOS DE TRAPECIOS Trap. rectángulo Trap. isósceles Trap. escaleno

23. 1.2 Trapecio isósceles Lados no paralelos iguales: AD = BC Ángulos basales iguales. Diagonales iguales: AC = BD Al trazar las alturas desde los vértices superiores, se forman en ambos extremos del trapecio dos triángulos rectángulos congruentes: AF = EB AB//CD AFD = BEC ~

24. Ejercicio de aplicación: 1. Determinar el área del trapecio isósceles ABCD. Solución: Al trazar las alturas desde los vértices superiores, se forman los triángulos rectángulos AED y BFC de ángulos: 30°, 60° y 90°. Además, como el trapecio es isósceles, AE=FB.

25. Área = (11 + 5) ∙ 3 2 Área = 8 ∙ 3 Área = 24 Área = (AB + DC) ∙ h 2

26. 1.3 Trapecio Rectángulo Tiene 2 ángulos rectos  = 180° h E AB//DC DA: altura del trapecio (DA = CE = h)

27. Todos sus lados son distintos 1.4 Trapecio Escaleno AB//DC

28. Ejercicios de aplicación: Solución: MN = 11 11 MN = 12 + 10 2 En el trapecio ABCD de la figura, MN es mediana. Determinar la razón entre el área del trapecio MNCD y el área del trapecio ABNM. MN = AB + DC 2 Si MN es mediana, entonces:

29. Luego, la razón (división) entre las áreas de los trapecios es: La mediana dimidia a la altura, entonces h 1 = h 2 . Área ABNM = (AB + MN ) ∙ h 2 2 Área MNCD Área ABNM = (11 + 10) ∙ h 1 2 = 21 ∙ h 1 2 = (12 + 11) ∙ h 2 2 = 23 ∙ h 2 2 = 21 ∙ h 1 2 23 ∙ h 2 2 = 21 23 Área MNCD = (MN + CD ) ∙ h 1 2

30. 2. Trapezoides 2.1 Características Generales No tienen lados paralelos. Tipos de Trapezoides: Asimétrico Simétrico (Deltoide)

31. 2.2 Trapezoide Simétrico (Deltoide) Está formado por 2 triángulos isósceles con base común: El área se puede calcular como: ADC y ABC, triángulos isósceles de base AC Las diagonales son perpendiculares: AC DB Área = (AC ∙ DB) 2 La diagonal DB dimidia a la diagonal AC (AE = EC) La diagonal DB es bisectriz del ángulo ADC y del ángulo CBA.

32. Ejercicio de aplicación: Solución: Luego, x= 35°. 1. En el trapezoide simétrico ABCD de la figura, BD es base. Determinar la medida del ángulo x. Los triángulos BAD y BCD son isósceles de base BD. Además, las diagonales son perpendiculares y AC: bisectriz del ángulo DCB.

33. 2.3 Trapezoide Asimétrico Lados distintos y ángulos interiores distintos. Para calcular su área, se descompone en figuras conocidas (triángulos, cuadrados, rectángulos, etc.) A C D B