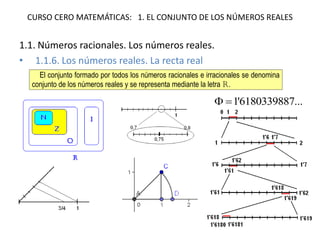
Este documento resume los principales tipos de números reales, incluyendo racionales e irracionales. Explica que los números reales (R) están formados por todos los números racionales e irracionales. También describe las propiedades de los intervalos, semirrectas y entornos de números reales, así como las operaciones con potencias, radicales y expresiones decimales de números racionales.







![CURSO CERO MATEMÁTICAS: 1. EL CONJUNTO DE LOS NÚMEROS REALES
1.2. Intervalos, semirrectas y entornos. Operaciones
• 1.2.3. Intervalos y semirrectas.
Intervalo cerrado de extremos a,b: se designa por [a,b] y esta
definido por }/{],[ bxaRxba , son los números reales
comprendidos entre a y b incluidos los extremos.
Intervalo abierto de extremos a,b: se designa por (a,b) y esta definido
por: }/{),( bxaRxba , son los números reales
comprendidos entre a y b excluyendo los extremos.
Intervalos semiabiertos (a,b] y [a,b) están definidos por:
}/{],( bxaRxba }/{),[ bxaRxba
Semirrectas
}/{),( axRxa }/{],( axRxa
}/{),( axRxa }/{),[ axRxa ](https://image.slidesharecdn.com/curso-160129001648/85/Curso-9-320.jpg)

![CURSO CERO MATEMÁTICAS: 1. EL CONJUNTO DE LOS NÚMEROS REALES
1.2. Ejercicios
1. Dados los siguientes conjuntos de números reales, ordenarlos de menor a mayor:
a.
2
7
,
12
1
,
4
3
,
3
2
y
6
1
b. 867'1,76'1,,
y 869'1
c. 838'3,38'3,83'3,4'3
y 140'3
2. Intercalar tres números reales de forma ordenada entre los pares de números siguientes:
a) 103'1,20'1
b) 203'3,20'3
.
3. Realizar las siguientes operaciones con intervalos y representar el resultado obtenido:
a) [-5,5] (0,6) b) [-5,5] (0,6)
c) (4,9](5,8] d) (4,9](5,8]
e) (-,0)(-1,4] f) (-,0)(-1,4]
g) (-3,4](2,+) h) (-3,4](2,+)](https://image.slidesharecdn.com/curso-160129001648/85/Curso-11-320.jpg)