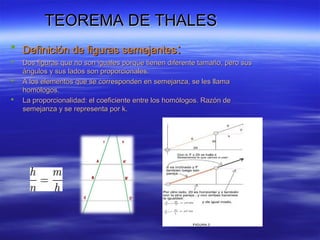
Este documento explica dos teoremas geométricos fundamentales. El Teorema de Tales establece que si dos figuras tienen ángulos y lados proporcionales, son semejantes. Se aplica para calcular distancias y alturas usando triángulos semejantes. El Teorema de Pitágoras expresa la relación entre los lados de un triángulo rectángulo. Se usa para resolver problemas sobre hipotenusas y catetos.

2. TEOREMA DE THALESTEOREMA DE THALES
 Definición de figuras semejantesDefinición de figuras semejantes::
 Dos figuras que no son iguales porque tienen diferente tamaño, pero susDos figuras que no son iguales porque tienen diferente tamaño, pero sus
ángulos y sus lados son proporcionales.ángulos y sus lados son proporcionales.
 A los elementos que se corresponden en semejanza, se les llamaA los elementos que se corresponden en semejanza, se les llama
homólogos.homólogos.
 La proporcionalidad: el coeficiente entre los homólogos. Razón deLa proporcionalidad: el coeficiente entre los homólogos. Razón de
semejanza y se representa por k.semejanza y se representa por k.

3. APLICACIÓN DEL TEOREMAAPLICACIÓN DEL TEOREMA
DE THALESDE THALES..

4. La escala es una razón de semejanza entre objeto, espacio, etc. Se utiliza para mapas, planos,La escala es una razón de semejanza entre objeto, espacio, etc. Se utiliza para mapas, planos,
maquetas, etc.maquetas, etc.
- Escala numérica: se escribe en forma lineal la relación entre el plano y la realidad. 1:100.000Escala numérica: se escribe en forma lineal la relación entre el plano y la realidad. 1:100.000
- Escala gráfica: se representa en una regla que indica las distancias equivalentes.- Escala gráfica: se representa en una regla que indica las distancias equivalentes.
- Un mapa es la ilustración de la parte terrestre a la realidad.Un mapa es la ilustración de la parte terrestre a la realidad.
- Las maquetas: son representaciones tridimensionales a escala reducida.Las maquetas: son representaciones tridimensionales a escala reducida.

5. APLICACIONES DELAPLICACIONES DEL
TEOREMA DE THALES 2TEOREMA DE THALES 2
Calculo alturas y distanciasCalculo alturas y distancias::
La semejanza de los triángulos seLa semejanza de los triángulos se
puede aplicar para resolver lapuede aplicar para resolver la
distancia entre dos puntos odistancia entre dos puntos o
determinadas alturas.determinadas alturas.
Método espejoMétodo espejo::
Mediante el reflejo de un objeto en unaMediante el reflejo de un objeto en una
superficie aplicando las propiedadessuperficie aplicando las propiedades
de los triángulos semejantes sede los triángulos semejantes se
pueden calcular las alturas de otropueden calcular las alturas de otro
objeto.objeto.

6. TEOREMA DE PITAGORASTEOREMA DE PITAGORAS
 Se define como la relación existente entra las longitudes de los lados de un triánguloSe define como la relación existente entra las longitudes de los lados de un triángulo
rectángulo.rectángulo.
 Es una igualdad que relaciona las longitudes de los tres lados de un triánguloEs una igualdad que relaciona las longitudes de los tres lados de un triángulo
rectángulo.rectángulo.
 En todo triángulo rectángulo se conocen como catetos a los que forman el ánguloEn todo triángulo rectángulo se conocen como catetos a los que forman el ángulo
recto y el lado opuesto es la hipotenusa.recto y el lado opuesto es la hipotenusa.

7. APLICACIÓN DEL TEOREMAAPLICACIÓN DEL TEOREMA
DE PITAGORAS.DE PITAGORAS.

8. 27/05/13 María Moreno 8
BibliografíaBibliografía
 Teorema de tales:Teorema de tales: http://www.vitutor.com/geo/eso/ss_1.htmlhttp://www.vitutor.com/geo/eso/ss_1.html
 Aplicación teorema de tales:Aplicación teorema de tales:
 http://www.google.es/search?http://www.google.es/search?
q=aplicacion+teorema+de+tales&hl=es&tbm=isch&tbo=u&source=univ&sa=X&ei=-q=aplicacion+teorema+de+tales&hl=es&tbm=isch&tbo=u&source=univ&sa=X&ei=-
hiNUZzkDMOAhQf_m4HICA&ved=0CEIQsAQ&biw=1024&bih=571hiNUZzkDMOAhQf_m4HICA&ved=0CEIQsAQ&biw=1024&bih=571
 Teorema de Pitágoras:Teorema de Pitágoras:
 Aplicación teorema de Pitágoras:Aplicación teorema de Pitágoras:
http://mimosa.pntic.mec.es/clobo/geoweb/trian9.htmhttp://mimosa.pntic.mec.es/clobo/geoweb/trian9.htm
http://www.ditutor.com/geometria/triangulos_semejantes.htmlhttp://www.ditutor.com/geometria/triangulos_semejantes.html