1) La derivada de una función en un punto representa la pendiente de la recta tangente a la curva gráfica de la función en ese punto, si existe y es finita. 2) Una función vectorial es derivable en un punto si y solo si cada una de sus componentes es derivable en ese punto. La recta tangente a una curva en R3 es la recta dada por la dirección del vector derivado en ese punto. 3) Los puntos regulares de una curva son aquellos en los que existe recta tangente, mientras que los puntos singulares son aquellos

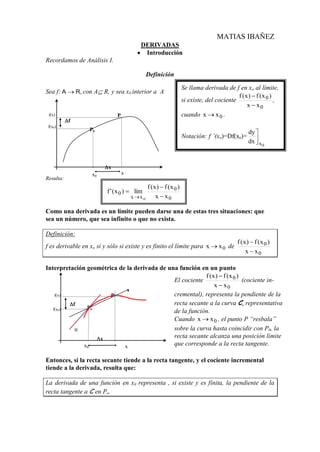
1. MATIAS IBAÑEZ
DERIVADAS
 Introducción
Recordamos de Análisis I.
Definición
Se llama derivada de f en xo al límite,
Sea f: A  R, con A R, y sea x0 interior a A
f (x)  f (x 0 )
si existe, del cociente ,
x  x0
f(x) P cuando x  x 0 .
f
f(x0)
Po
dy 
Notación: f ’(xo)=Df(xo)=
dx  x
 0
x
x0 x
Resulta:
f (x)  f (x 0 )
f ' ( x 0 )  lím
x x o x  x0
Como una derivada es un límite pueden darse una de estas tres situaciones: que
sea un número, que sea infinito o que no exista.
Definición:
f (x)  f (x 0 )
f es derivable en xo si y sólo si existe y es finito el límite para x  x 0 de
x  x0
Interpretación geométrica de la derivada de una función en un punto
f (x)  f (x 0 )
El cociente (cociente in-
x  x0
s
f(x) P cremental), representa la pendiente de la
f recta secante a la curva C, representativa
f(x0) Po
de la función.
Cuando x  x 0 , el punto P “resbala”
tt sobre la curva hasta coincidir con P0, la
x recta secante alcanza una posición límite
x0 x que corresponde a la recta tangente.
Entonces, si la recta secante tiende a la recta tangente, y el cociente incremental
tiende a la derivada, resulta que:
La derivada de una función en x0 representa , si existe y es finita, la pendiente de la
recta tangente a C en Po.
define como tangente a la curva en Po.

2. MATIAS IBAÑEZ
 Derivada de función vectorial

Consideremos f :A Rn con A  R  n  2 , y t0 pto. interior de A
I.1.-Definición:
 
 f (t 0  t )  f (t 0 )
Se llama vector derivado de f en t0 al límite, si existe de: , cuando t
t

 0. Se indica f '(t 0 ) .
 
 f (t 0  t )  f (t 0 )
Resulta: f '(t 0 ) = lím
t 0 t
Teorema:

f (t)= (f1(t);f2(t);.....;fn(t)) es derivable en t0  fi (t) es derivable en t0, i{1,...,n}
Demostración:
Por def. de
derivada
 
 f ( t 0  t )  f ( t 0 ) Por def.
f (t) derivable en t0   lím 
t  0 t de f
(f1 ( t o  t ); f 2 ( t o  t );f n ( t o  t ))  (f1 ( t o ); f 2 ( t o );f n ( t o ))
 lím 
t  0 t
f1 (t o  t )  f1 (t o );....; f n (t o  t )  f n (t o )
 lím 
t  0 t Por límite de
 f ( t  t )  f1 ( t 0 ) fn( t 0  t )  fn( t 0 )  una función
  lím 1 0
 t  0 ;; lím  
 vectorial
Por def. de vec-
 t t  0 t  tor y de deriv. de
una función
escalar
f1 ( t 0  t )  f1 ( t 0 ) f n ( t 0  t )  f n ( t 0 )
 lím = f1’(t0)  ........  lím =f ’(t )
n 0
 t 0 t  t 0 t
Recta tangente y plano normal a una curva en R3

Consideramos f :A Rn continua ,con A  R  n = 3. La representación gráfica del
conjunto imagen es una curva en R3

3. MATIAS IBAÑEZ
P  
 f (t0  t )  f (t0 )
z f (t 0  t )
P0

f (t 0 )
y
x
 

Consideremos los puntos P y P0 definidos por f ( t 0  t ) y por f ( t ) ;el vector f (t0  t )  f (t0 )

0
tiene el módulo y la dirección de la cuerda PP0 .
Al dividir por t y tomar el límite para t0, el vector derivado, si existe, tendrá la dirección
límite de la de una cuerda cuyo extremo tiende a coincidir con el punto inicial , es decir tendrá
la dirección tangente a la curva en P0 . 
Resulta que la recta tangente a la curva representativa de la imagen de f (t ) en P0 , es

la recta que tiene la dirección de f '(t 0 ) y a la que pertenece P0.
  
t P0  X  f (t 0 )   f ' (t 0 ) (ec. vectorial de la recta tg.)
o bien ,si fi’(t0)0,i{1,2,3} :
x  f1 ( t 0 ) y  f 2 ( t 0 ) z  f 3 ( t 0 )
  (ecs. simétricas de la recta tangente)
f1 ' ( t 0 ) f 2 ' (t 0 ) f 3 ' (t 0 )
Si llamamos N al plano perpendicular a la recta tangente en P0, es decir al plano normal a la

curva asociada a la imagen de f (t ) , resulta que la ecuación vectorial de N es:
  
X  f (t 0 ) f ' (t 0 )  0
y la ecuación cartesiana:
f 1’(to).(x- f1(to)) + f 2’(to).(y- f2(to)) + f 3’(to).(z- f3(to)) =0
 Puntos regulares y singulares de una curva. Curvas regulares y lisas.
 
Un punto P0  C es un punto regular de C si y sólo si existe la recta tangente a C en P0 .
 
Para ello debe existir una función vectorial f :[a,b]  R con n  2, continua / f (t)=
n

4. MATIAS IBAÑEZ
(f1(t);f2(t);.....;fn(t)) siendo C la curva asociada a su imagen, tal que exista y no sea nulo el vec-

tor derivado f ‘ (to) con
 
P0 = f (t0). Los puntos de C que no son regulares se llaman puntos singulares .
Toda curva admite distintas parametrizaciones, puede ocurrir que en alguna de ellas el
vector derivado sea nulo, pero que no lo sea para otra.

Si f es inyectiva en [a,b], la curva es simple.

Si t[a,b] es f ’ (t) continua y distinta del vector nulo, entonces la curva

C asociada al conjunto imagen de f es lisa.
 Derivación de campos escalares
Campos escalares de dos variables
INCREMENTO PARCIAL Y TOTAL

Sea F: AR, con A R2 / z = F(x;y) y sea P0 =(a;b) interior a A
Se llama incremento parcial de "F " debido a "x" (se escribe:  x F ) al incremento
que experimenta la función cuando se provoca una variación "h" ó “ x ” de la variable "x" y
se mantiene constante la variable "y".
Es decir:  x F = F(a + h ; b) - F(a;b)= F(a + x ; b) - F(a;b)
Gráficamente significa cortar la superficie representativa de z=F(x;y), con el plano y =
b y medir la variación de la función sobre la curva intersección. En el dibujo: |  x F |= medida
de TT'
z |  y F | = medida de| MM ' |
Q
M
T’ M’
S’
T
S
b y
b+k
a
a+h
x

5. MATIAS IBAÑEZ
Con el mismo criterio, la variación de "F" debida a "y",(  y F ) se obtiene considerando x
= cte y provocando un incremento "k" ó “  y ”sobre el eje "y".
Es decir:  y F = F(a;b + k) - F(a;b)= F(a; b+  y ) - F(a ; b)
Estos incrementos  x F y  y F reciben el nombre de incrementos parciales.
Si provocamos simultáneamente variaciones en x e y , que llamaremos "h" y "k",(ó  x ,  y
respectivamente) ,obtendremos el incremento total de F
Entonces :  F = F(a + h; b + k) - F(a;b)= F(a +  x ; b +  y ) - F(a;b)
Gráficamente este incremento mide la variación que experimenta z, sobre la curva que resulta
de cortar la superficie representativa de  = F(x;y) con un plano perpendicular al plano xy,
z
según la dirección de la recta P0P con P =(a + h; b+ k) (En el dibujo:| F |= medida de
SS' ).
 Derivadas parciales:

Sea F: AR, con A R2 / z = F(x;y) y sea P0 =(a;b) interior a A

Se llama derivada parcial con respecto a x de F(x;y) en (a;b) ( ó en P0 ), al límite para  x 
0, del cociente entre  x F y  x
F F ( a  x; b)  F ( a; b) F ( a  h; b)  F ( a; b)
F' x (a;b) =   lím  lím
x x  0 x h 0 h
P 0
Análogamente:
F F ( a ; b  y )  F ( a; b) F ( a ; b  k )  F ( a; b)
F' y (a;b) =   lím  lím
y y  0 y k 0 k
P 0
Observemos que F' x (a;b) se calcula manteniendo y = cte y F' y (a;b), con x = cte.
De la definición se deduce que las reglas para calcular derivadas parciales son las mismas que
se utilizan para calcular derivadas de funciones escalares.
Geométricamente las derivadas parciales representan las pendientes de las rectas tangentes a
las curvas que se obtienen como intersección de la superficie con planos y= cte ó x = cte,
según corresponda, en el punto (a;b;F(a;b))
z
F’y (a;b)= mt = tg 
y
b
a
x

6. MATIAS IBAÑEZ
Ejemplo:
 xy
 si ( x; y)  (0;0)
Calcular las derivadas parciales en (0;0) de F(x;y)=  x 2  y 2
0 si ( x; y)  (0;0)

Recurrimos a la definición:
F  F(a  h; b)  F(a; b)
   lím
x  P h 0 h
0
h.0
0
F  F(0  h;0)  F(0;0) F  22 00
   lím    lím h  0  lím 0
 x  (0;0) h  0 h  x  (0;0) h  0 h h 0 h
F  F(a ; b  k )  F(a; b) F  F(0 ; k )  F(0;0)
   lím    lím 
y P k 0 k  y  (0;0) k  0 k
0
0.k
0
F 2 2
 lím 0  k 0
y (0;0) k  0 k
Observación:
En la página 20, se trabajó con la misma función y se comprobó que no existe límite doble
para (x;y)(0;0), por lo tanto no es continua en (0;0).
Estos significa que, para campos escalares, la existencia de las derivadas parciales no es una
condición tan fuerte como la derivabilidad para funciones de una variable.
En efecto, para funciones escalares: derivabilidad continuidad; sin embargo, para
campos escalares, este ejemplo nos muestra que un campo puede tener derivadas
parciales en un punto en el que no es continuo.
Cuando no hay problemas en la definición de la función, puede derivarse utilizando las reglas
y fórmulas conocidas. Para derivar respecto de “x” , se piensa que “y” es constante; mientras
que para derivar respecto de “y”, se trabaja con “x” constante.
Por ejemplo:
Si F(x;y)= 2x.sen(xy)+ y2 , resulta:

7. MATIAS IBAÑEZ
F’x= 2 sen(x.y)+ 2xy cos(x.y) ; F’y = 2x cos(xy) + 2y.
2
 Derivada direccional


Sean F:A  R n  R con A abierto , Po  A y v versor de Rn
Definición
 
Si llamamos v al versor que tiene la dirección y sentido de Po P , podemos decir que existe t 
  
R/ Po P = t v . Entonces definimos como derivada direccional de F en la dirección de v
  
 F (Po  t v)  F(Po )  
en Po al límite para t 0 de . (La indicamos F’ ( Po ; v ) .
t
  
  F (Po  t v)  F(Po )
Resulta: F’( Po ; v ).= lím ( con t  R)
t 0 t
 Interpretación geométrica
Al tomar una derivada direccional en un punto con respecto a un versor, se están consi-
derando variaciones de la función sobre la recta que pasa por el punto y es paralela al
versor.
z
y
b

v
a Po

x s
 
La derivada direccional de F en Po con respecto al versor v , representa la pendiente de
la recta tangente a la curva intersección entre la sup. representativa de z=F(x;y) y el pla-
no paralelo al eje z, que corta al plano (x,y) según la recta s (es decir, la recta que pasa
 
por Po y es paralela al versor v ).

8. MATIAS IBAÑEZ
OBSERVACIONES :
a) Si se trabaja con el versor opuesto, si bien el punto es el mismo, la recta “s” también,
y la curva intersección y , por lo tanto la recta tangente, no varían, cambia el ángulo
que se vincula con la pendiente.
y

-  x
v

v
 
b) Si se toman las derivadas con respecto a los versores i y j , se obtendrán las derivadas
parciales respecto de x e y respectivamente.
Ejemplo:
     2 2
Calcular F’( P o ; v ) siendo F(x;y) = x2 –2xy; Po =(1;1) y v = 
 2 ; 
 2 

  
  F (Po  t v)  F(Po )   F(1  t. 2 ;1  t. 2 )  F(1;1)
F’( Po ; v ).= lím F’( Po ; v ).= lím 2 2
t 0 t t 0 t
 
2
 2  2  2
1  t   21  t 1  t   12  2.1.1
    2 
 
F’( Po ; v ).= lím  2   2  
t 0 t
 
F’( Po ; v ).= lím
1 t 2  t
2
2
 2  t 2  (1)
= lím

t.  2t3 
2  2
t 0 t t 0 t
 Campos escalares en general

Consideremos F:A R, con ARn , un punto X 0 interior a A y un vector unitario (ver-

sor) v de Rn.

9. MATIAS IBAÑEZ
Derivada direccional
 
Llamamos derivada direccional de F en la dirección de v en X 0 al límite para
  
F( x 0  t v)  F( x 0 )  
t 0 de . La indicamos F’( x 0 ; v) .
t   
  F( x 0  t v)  F( x 0 )
Resulta: F’( x 0 ; v) .= lím ( con t  R)
t 0 t
 Derivada de un campo escalar respecto de un vector: Definición
 
Consideremos F:A R, con ARn , X 0 un punto interior a A y un vector v de Rn.
 
Llamamos derivada de F en X 0 con respecto a la dirección de v al límite, si existe de:
  
  F ( x0  t . v )  F ( x0 )
F’( x0 ; v ) .= lím ( con t  R)
t 0 t
OBSERVACIÓN:
En la derivada direccional se trabaja con un vector unitario
En la derivada con respecto a un vector, se consideran vectores cualesquiera. Al calcular

derivadas en un punto respecto de vectores de la forma  v que, obviamente correspon-
den a la misma dirección, se obtienen, en un mismo punto distintos valores para la deri-
vada .
 Teorema del valor medio
Recordamos el teorema de Lagrange ( o del valor medio del cálculo diferencial) para
funciones escalares
Si f es continua en [a,b] , derivable en (a,b) , entonces existe un punto “ c” interior al
intervalo (a,b) tal que la variación que experimenta la función al pasar de “a” a “b”
es igual al producto de la derivada de f en dicho punto “c” por la amplitud del interva-
lo.
y t
B Geométricamente significa que si f es continua en un
f(b) intervalo cerrado [a,b] y derivable en (a,b), entonces
f
existe un punto en el arco representativo de f) en el
r
que la recta tangente es paralela a la cuerda que une
los extremos del arco.
A
f(a)
a c b x

10. MATIAS IBAÑEZ
 Teorema del valor medio para campos escalares:
 
Consideremos F:A R, con ARn tal que exista F’ ( x ; v ) en un subconjunto de A al
   
que pertenezcan x o y x o + t v , siendo v un vector unitario de Rn.
Entonces se cumple que :
     
 c (0,t) / F( x o + t v )- F( x o ) = t . F’( x o + c v , v )
Demostración:
 
Trabajaremos con la función de una variable  (t) = F( x o + t v ) con t  [0,t]
    
Como existe F’( x o ; v ) en un subconjunto de A al que pertenezcan x o y x o + t v
En R2 sería:  
xo + tv

 v A
xo

11. MATIAS IBAÑEZ
Resulta:
  (t) continua en [0,t] (por que para funciones de una variable se cumple que
si es derivable es continua)

  (t) derivable en (0,t) (trabajamos en [0,t] porque (0)=F( x o )y 
 
(t)=F( x o + t v )
Por el T. del valor medio para funciones de una variable, se cumple que:
 c entre 0 y t /  (t) -  (0) = t. ‘ (c)
Calculamos , por def. ’(c)
   
(c  )  (c) F(x 0  (c  )v)  F(x 0  cv)
' (c)  lím  lím 
 0   0 
    
F[(x 0  cv)  v]  F(x 0  cv)   
' (c)  lím  F' (x 0  cv; v)
 0 
Reemplazando se tiene que:
     
 c entre 0 y t / F( x o + t v )- F( x o ) = t . F’( x o + c v ; v )
 Propiedad de homogeneidad de la derivada direccional.
 
Consideremos F:A R, con ARn , entonces R, F’( x o ;  v ) y se cumple que:
   
F’( x o ;  v ) = F’( x o ; v )
Demostración:
Por definición de derivada direccional:
   
 
  F( x 0  t v)  F( x 0 ) F( x 0  t v)  F( x 0 )
F’( x o ;  v ) = lím = lím   =
t 0 t t 0 t
multiplicamos y dividimos por 
  
  F( x 0  t v)  F( x 0 )  
F’( x o ; v ) =  lím  =  F’ ( x o ; v ) ( por def. de deriv.)
t 0 t
   
Luego: F’( x o ;  v ) =  F’ ( x o ; v )
 Aditividad de las derivadas direccionales
 
Consideremos un campo escalar F: A R con ARn  n  2, y sean u y v dos versores

de Rn respecto de los cuales F tiene derivadas direccionales continuas en x o
        
Si w  u  v , entonces existe F’( x o ; w ) = F’( x o ; u ) + F’( x o ; v )

12. MATIAS IBAÑEZ
Por definición de derivada respecto de un vector:
      
  F( x 0  t w)  F( x 0 ) F( x 0  t (u  v))  F( x 0 )
F’( x o ; w ) = lím = lím =
t 0 t t 0 t
   
F( x 0  t u )  t v)  F( x 0 )
= lím
t 0 t
 
Sumamos y restamos en el numerador F ( x0  t u ) y agrupamos convenientemente , en-
tonces:
       
  F[(x 0  t u )  t v]  F(x 0  t u)  F(x 0  t u)  F( x 0 )
F’( x o ; w ) = lím =
t 0 t
       
F( x 0  t u )  F( x 0 ) F[( x 0  t u )  t v] F( x 0  t u )
= lím  lím
t 0 t t 0 t
 
En el primer sumando tenemos, por definición: F’( x o ; u ); y en el numerador del segundo
aplicamos el T. del Valor medio:
   
    t. F'[ x o  t u   v; v]
F’( x o ; w )= F’( x o ; u ) + lím con  entre 0 y t.
t 0 t
0  t
Resulta que cuando t0, también 0,entonces, por la continuidad pedida a las deriva-
das direccionales se tiene:
     
F’( x o ; w )= F’( x o ; u ) + F’( x o ; v )
 Las derivadas parciales como casos particulares de derivadas direccionales
Si para el campo escalar F: A R con ARn  n  2, se calculan las derivadas direc-
cionales con respecto a los versores de la base considerada, se obtienen las derivadas
parciales.
 i = n 
Es decir que si a x o =  i ei , se le aplica derivada de F en la dirección de ei se obtie-
i=1
ne la derivada parcial de F en la dirección de e i .
  
  F ( x0  t ei ) F ( x0 )  F 
F ‘ ( x o , ei ) = lím = 
t 0 t  xi  

X0

13. MATIAS IBAÑEZ
 Cálculo de derivadas direccionales en función de las derivadas parciales

Consideremos un campo escalar F: A R con ARn  n  2, y sea v un versor de Rn .

Supongamos además que F tiene derivadas parciales continuas en x o .
Como las componentes de un versor son los cosenos directores del mismo:
n


v =  cos  i ei , utilizando las propiedades de homogeneidad y aditividad de las deri-
i=1
vadas direccionales se tiene:
n
n  
F’( x o ; v )= F’( x o ;  cos  i ei ) =  cos  i F’( x o ; ei )
   
i =1 i=1
Para campos escalares de tres variables, con derivadas parciales continuas es:
    
F’( x o ; v )= F’x( x o ). cos 1 + F’y( x o ). cos 2 + F’z( x o ). cos 3

siendo v = cos 1 i + cos 2 j + cos 3 k
 Gradiente
Consideremos un campo escalar F: A R con ARn  n  2 con derivadas parciales
respecto de todas sus variables en todo punto de B  A Rn.
Se llama gradiente de F al campo vectorial definido de B en Rn mediante:
 F  F  F
Grad. F =  ; ;....  .
  x1  x2  xn 

También se utiliza para designarlo al “operador” nabla:  F = Grad. F
Relación entre el vector gradiente y la derivada direccional

Consideremos F: A R con ARn  n  2, ,sea v un versor de Rn expresado a partir
n


de sus cosenos directores, Es decir: v =  cos  i ei
i=1

Supongamos además que F tiene derivadas parciales continuas en x o .punto interior de
A.
Vimos que la derivada direccional puede expresarse en función de las derivadas parciales

14. MATIAS IBAÑEZ
n  F
 
F’( x o ; v )=  cos  i .
 xi  X

.
i=1
0
  n F

Como el vector gradiente de F en x o es:  F ( x0 ) =  . e , se tiene que la deri-
 xi  i
i=1
 
vada direccional en x o es igual al producto escalar entre el vector gradiente de F en x o y el
   
versor v . Significa que la derivada direccional en x o es la proyeccción del F ( x o )

sobre v .
     
Proyv (  F ( x0 ) ) =  F ( x0 ) . v (pues proyectar un vector sobre otro significa multiplicarlo
escalarmente por el versor correspondiente)
Pero el segundo miembro coincide con la fórmula obtenida para la derivada direccional,
entonces:
F    v
 ( x 0 )  F( x 0 ). v
v

Si F tiene derivadas parciales continuas en x o la derivada direccional de F en la dirección
   
de v en x o es igual a la proyección del vector gradiente de F en x o sobre v .
(Recordar que la proyección de un vector sobre otro es un número).
Ejemplo:
Verificamos el resultado obtenido en la página 31
     2 2
Calcular F’( P o ; v ) siendo F(x;y) = x2 –2xy; Po =(1;1) y v = 
 2 ; 2 

 
Como F es polinómica, podemos asegurar que tiene derivadas parciales continuas y, por
lo tanto es válido aplicar la fórmula de derivada direccional en función del gradiente.

F’x= 2x-2y  F’x( Po )=0
 
  F(Po )  (0;2)

F’y= -2x  F’y( Po )= -2
      2 2
Resulta: F’( P o ; v )=   F(Po )  v  (0;2)   
 2 ; 2  2
 
Por otra parte , la proyección de un vector sobre otro es máxima cuando las direcciones
de ambos coinciden; mínima cuando los vectores son de la misma dirección pero tienen
sentidos opuestos y nula cuando las direcciones son perpendiculares. Entonces:
 La derivada direccional es máxima en la dirección y sentido del vector gradiente.
Como en ese caso cos = 1, resulta que el valor de la máxima derivada direccio-
nal en un punto es el del módulo del gradiente en dicho punto.

15. MATIAS IBAÑEZ
 F   
máx.  ( x0 )   F ( x0 )
 v
 La derivada direccional es mínima en la dirección del vector gradiente pero en
sentido opuesto. Como en ese caso cos = - 1, resulta que el valor de la mínima
derivada direccional en un punto es menos el módulo del gradiente en dicho
punto.
F   
(mín.  ( x 0 )    F ( x 0 )
v
 La derivada direccional en un punto es cero en la dirección perpendicular a la
del vector gradiente en dicho punto. (Las direcciones son perpendiculares si y sólo
si el producto escalar es nulo).
( Para campos escalares de dos variables, recordar que cos  2 = sen  1)
Ejemplos:

Dados los siguientes campos escalares y el punto Po que en cada caso se indica, hallar la

o las direcciones en las que la derivada direccional en Po es máxima .
1 x2 
a) F(x;y)=  en Po =(2;-2)
x y
1 2x
F’x =  
x2 y continuas en Po ,la dirección de máxima derivada está dada por el vec-
x2 
F’y = tor gradiente en Po
2
y
 
 F(Po ) =(-5/2;1)
  5 
  ;1
F(Po )  2    5 1 
Luego la dirección de máxima derivada es v  =  ; 
  29  29 29 
F(Po )
2
 xy 2
 si ( x; y)  (0;0) 
b)1F(x;y)=  x 2  y 2 en Po =(0;0)

0 si ( x; y)  (0;0)
Por la forma en que está definida la función, es más sencillo obtener la derivada direccio-
nal por definición que analizar si las derivadas parciales son o no continuas.

Supongamos que consideramos un versor genérico de R2 , u  (h; k ) .
1
Ejercicio de final. Tema 11 .1.b)

16. MATIAS IBAÑEZ
Resulta:
  
  F(Po  t u )  F(Po )   F( th; tk)  F(0;0)
F' (Po ; u )  lím  F' (Po ; u )  lím
t 0 t t 0 t
th.( tk) 2 t 3 hk 2
0
  ( th) 2  ( tk) 2 t 2 (h 2  k 2 ) hk 2
F' (Po ; u )  lím  lím   hk 2 pues h2+k2=1,
t 0 t t 0 t h2  k2

ya que u  (h; k ) es un versor.
Este resultado nos permite asegurar que la función tiene derivada en cualquier dirección
y sentido. Podemos escribir esta derivada en función de h:
 
F’( Po ; u ) =h(1-h2)=h-h3
Como se pide la o las direcciones en la que la derivada direccional es máxima, y la fun-
ción a maximizar es de una variable, se buscará el valor de h que anula la derivada prime-
ra y que hace negativa a la derivada segunda.
Es decir:
Sea  (h)= h – h3, entonces ’ (h)= 1-3h2
1
1-3h2 =0  |h|= . Pero ” (h)=-6h, permite asegurar que la derivada direccional es
3
1
máxima cuando h= .
3
2
Como | k| = 1 h 2 , se tiene |k| = . Entonces las direcciones en la que la derivada
3
 1 2  3 6  3 6
direccional es máxima son:  ;  =
 3 3  3 3   3;  y ; 
     3 

NOTA: Obsérvese que si se trabaja con el vector gradiente, la dirección de máxima
derivada en un punto es única. El haber obtenido dos direcciones indica que la fórmula
del gradiente no es aplicable en este caso.
Derivación de campos vectoriales :
 Derivada direccional: Definición
 
Consideremos F: A  R m , con A  R n , ( n  2, m  2) , un punto X 0  ( x1; x 2; ...;x n )
 
interior a A, v un vector de Rn, v su correspondiente versor.

17. MATIAS IBAÑEZ
  
Llamamos derivada direccional de F en la dirección de v en X o , al límite para t0
    
F( X 0  tv)  F( X o )
de .
t  

La indicamos F ' ( X 0 ; v).
    
   F( X 0  tv)  F( X o )
Resulta: F ' ( X 0 ; v). = lím con t  R
t 0 t

18. MATIAS IBAÑEZ
Derivación de campos vectoriales
 Derivada de un campo vectorial respecto de un vector.
  
Llamamos derivada direccional de F en X o , con respecto al vector v , al límite para
    
F( X 0  tv)  F( X o )
t0 d e .
t
    
   F( X0  tv)  F( Xo )
Es decir: F ' ( X0 ; v).= lím con t  R
t 0 t
Observación: al igual que en los campos escalares, en las derivadas direccionales se tra-
baja con vectores unitarios. En las derivadas respecto de un vector, se consideran vecto-

res cualesquiera. Al calcular derivadas en un punto respecto de vectores de la forma . v
que, obviamente corresponden a la misma dirección, se obtienen en un mismo punto,
distintos valores para la derivada.
 Propiedades de las derivadas direccionales de campos vectoriales
     
Sea F: A  R m , con A  R n , ( n  2, m  2) / F( X)  ( F1 ( X); F2 ( X);...; Fm ( X)) .
1) Con una demostración similar a la realizada para funciones vectoriales se tiene que:
        
F '( X , v )  ( F1 ' ( X , v ); F2 ' ( X , v );....Fm ' ( X , v ))

2) Si las F’i (con i {1,2,...,m} son continuas en X 0 , para cada componente vale la
homogeneidad y la aditividad de la 
   derivada direccional para campos escalares, entonces:

   
a) F '( X0 , v)  ( F1 '( X0 , v); F2 '( X0 , v);...; Fm, '( X0 , v)) 
     
  F1 '( X 0 , v); F2 '( X 0 , v);... Fm '( X 0 , v) 
        
 . F1 '( X 0 , v); F2 '( X 0 , v);...; Fm '( X 0 , v)  . F '  X 0 ; v
    
b)Si u y v son versores de Rn y w  u  v , entonces:
        
F '  X0 ; w  F '  X 0 ; u  F '  X 0 ; v
 Derivadas parciales de campos vectoriales

Si para el campo vectorial F: A  R m , con A  R n , ( n  2, m  2) , se calculan
las derivadas direccionales respecto de los versores de la base canónica, se obtienen las
derivadas parciales.
 n 
Consideremos X 0   x j . e j . A la derivada direccional de F con respecto a e j , se la
 
j1

llama derivada parcial de F con respecto a xj .

19. MATIAS IBAÑEZ
 F  
 1 
 x j  X 

 0 
F   
   
F X 0  te j
 
 F( X 0 )  F2  
   
F ' (Xo ; e j )    tlím0   x j   
 x j   t  X0 
X0   
 F  
 m 
 x j   
 X0 
 Matriz jacobiana o matriz derivada

Sea el campo vectorial F: A  R m , con A  R n , ( n  2, m  2) , se llama matriz jaco-
biana o matriz derivada a la matriz mxn cuyas filas son las derivadas parciales de cada
una de las componentes de F . La matriz jacobiana está definida en aquellos puntos de A

en los que están definidas todas las derivadas parciales de las componentes de F . La filas
de la matriz jacobiana son los gradientes de cada componente. Las columnas son los vec-
tores derivados del campo respecto de cada una de las variables.
 F1 F1 F1 
 x 
x 2 x n 
 F1 F2 F2 
   2  
D[ F( X)]   x1 x 2 x n 
    
 Fm Fm Fm 
  
 x1 x 2 x n 
Ejemplo:
 
Dado el campo vectorial F : R 3  R 2 / F ( x; y; z)  (2x 2 y  z;2z 2 x  3y) , se pide su
matriz derivada.

Consideramos F (x; y; z)  F1 ( x; y; z); F2 ( x; y; z)  , entonces:
 F1 F1 F1 
       4xy 2x 2 1 
D[ F ( X )]   x y z 
D[ F ( X )]   2 
 F2 F2 F2   2z 4zx 
 x   3 
 y z 

20. MATIAS IBAÑEZ
 Cálculo de derivadas direccionales en función de las derivadas parciales

Consideremos un campo vectorial F :A Rm, con ARn ,(n  2 ; m 2) , un punto
 n
X 0 interior a A , y un versor v   cos  j . e j de Rn
 
j=1

 F1 ( X ) 
  
  F2 ( X )  
Supongamos además que F ( X )=  tiene derivadas parciales continuas en X 0 ,
  
  
 Fm ( X ) 
    n  F 
entonces  i  { 1,2,....,m} , F’i ( X 0 ; v ) = Fi ( X 0 ) . v = 
 i
 . cos  j .
j=1  x j  
X
0
    
 F1 '( X 0 ; v )   F1 ( X 0 ). v 
      
   F2 '( X 0 ; v )   F2 ( X 0 ). v 
Luego: F '( X 0 ; v )   = 
     
      
 F ' m ( X 0 ; v )   Fm ( X 0 ). v 
 F1   F1   F1  
  
 x2  X  xn X 

 x1  X  
  cos  
0 0 0

 F2   F2   F2    1

 cos 
 x2 X  xn X  . 
      
F '( X 0 ; v )    x1  X    = D[ F ( X 0 ) ] . v
2
 0 0 0   
    
  cos  
n
 Fm   Fm   Fm  

 x2  X  xn  X 
 
 x1  X   
 0 0 0 
 
Luego , si F tiene derivadas continuas en X 0 se cumple que:
     
F '( X 0 ; v )  D[ F ( X 0 )] . v

21. MATIAS IBAÑEZ
Derivadas sucesivas o iteradas.
 De funciones vectoriales
 
La derivada de f : A  R m con A R /f (t )  (f1 (t ); f 2 (t );;f m (t )) se obtiene derivan-
do cada una de las componentes que son funciones escalares.
Por lo tanto si las f i con i {1,2,...m} tienen derivadas n-simas, podremos definir la
 
 
derivada n-sima de f mediante: f (n ) ( t )  f1 n ) ( t ); f 2n ) ( t );....f m ) ( t )
( ( (n
 De campos escalares.
Sea F:AR con A  Rn . Las derivadas parciales de F están definidas para todo punto
de B  A  Rn . Por lo tanto, para cada una de ellas podrá analizarse la existencia de
sus derivadas parciales que, si existen, serán las derivadas segundas de F. Así sucesiva-
mente, podrán definirse las derivadas n- simas de F.
Un campo escalar de n variables puede tener n derivadas primeras y en consecuencia n2
derivadas segundas, n3 derivadas terceras,....., nk derivadas k-simas. Bajo ciertas condi-
ciones, algunas de las derivadas iteradas son iguales.
Sea F:R2R/ F(x;y)= x2y + 3xy, podemos calcular
F’x(x;y)= 2xy + 3y F’ y(x;y)=x2 + 3x
Cada una de estas funciones puede ser derivada respecto de cada una de sus variables,
permitiéndonos obtener cuatro derivadas segundas:
F' x  2 F F' y  2F
  F"xx  2y   F" yx  2x  3
x x 2 x xy
F' x  2F F' y  2F
  F"xy  2x  3   F" yy  0
y yx y y 2
Las recuadradas son las que llamaremos derivadas cruzadas. Como vemos en este ejem-
plo resultan iguales.
Analicemos esas derivadas en (0;0) para el campo F:A  R2R/
 3yx2  2xy 2
 si ( x; y)  (0;0)
F(x;y)=  xy con A={(x;y)  R 2 /x  -y  ( x ;y)=(0;0)}
0 si ( x; y)  (0;0)


22. MATIAS IBAÑEZ
Debemos calcular las derivadas primeras. Si lo hacemos por fórmula para (x;y)(0;0) y
por definición en el origen obtenemos:
 3yx2  6xy 2  2 y 3
 si ( x; y)  (0;0)
F’x(x;y)=  ( x  y) 2 y

0 si ( x; y)  (0;0)
 3x 3  4x 2 y  2xy 2
 si ( x; y)  (0;0)
F’y(x;y)=  ( x  y) 2

0 si x; y   (0;0)
Entonces
F' x (0; k )  F' x (0;0)
F"xy (0;0)  lím 
k 0 k
3k.0 2  6.0.k 2  2k 3
0
(0  k ) 2  2k 3
F"xy (0;0)  lím  lím  2
k 0 k k 0 k3
Del mismo modo:
F' y (h;0)  F' y (0;0)
F" yx (0;0)  lím 
h 0 h
3h 3  4.h 2 .0  2h.0 2
0
(h  0) 2 3h 3
F" yx (0;0)  lím  lím 3
h 0 h h 0 h3
En este ejemplo, como vemos las derivadas cruzadas en (0;0) son distintas.
 Teorema de Schwarz
Consideremos un campo escalar de dos variables F : AR con A  R2 /

existan F’x , F’y y F”xy en un entorno de X 0  ( x0 ; y0 ) punto interior de A.
  
Entonces, si F”xy es continua en X 0 , existe F”yx y se cumple que F”yx( X 0 )=F”xy( X 0 ).
(En el ejemplo falla la continuidad de las derivadas primeras
La propiedad subsiste para cualquier número de variables, ya que en la derivación res-
pecto de dos de ellas se mantienen constantes las demás. Si se cumplen las hipótesis del

23. MATIAS IBAÑEZ
T. de Schwarz , de las n2 derivadas segundas que tiene un campo escalar de n variables ,
n(n  1)
sólo son distintas.
2
Pueden enunciarse condiciones similares para las derivadas sucesivas de orden superior. Si
tales condiciones se cumplen , el número de derivadas k-simas distintas será el de
combinaciones con repetición de “n” elementos tomados de a “k”., es decir el número
 n  k  1
combinatorio  
 k 
Por ejemplo, un campo escalar de 3 variables ( n = 3 ), tiene 15 derivadas parciales dis-
tintas de cuarto orden (k= 4).
 De campos vectoriales
Debe considerarse que las derivadas de campos vectoriales surgen de derivar cada
componente y las componentes de un campo vectorial son campos escalares.