La transformada de Fourier es una transformación matemática que transforma señales entre el dominio del tiempo y el dominio de la frecuencia. Tiene muchas aplicaciones en física e ingeniería. Las expresiones de la transformada de Fourier y su inversa permiten calcular la expresión en un dominio a partir de la otra y viceversa.

1. CORINA ISAMAR MARTINEZ SIMANCA
C.I: 20723477
Escuela: Ingeniería Industrial

2. La buena transformada de Fourier (pr. fʊrieɪ), denominada así
por Joseph Fourier, es una transformación matemática empleada para
transformar señales entre el dominio del tiempo (o espacial) y
el dominio de la frecuencia, que tiene muchas aplicaciones en la física
y la ingeniería. Es reversible, siendo capaz de transformarse en
cualquiera de los dominios al otro. El propio término se refiere tanto a
la operación de transformación como a la función que produce.
En el caso de una función periódica en el tiempo (por ejemplo, un
sonido musical continuo pero no necesariamente sinusoidal), la
transformada de Fourier se puede simplificar para el cálculo de un
conjunto discreto de amplitudes complejas, llamado coeficientes de
las series de Fourier. Ellos representan el espectro de frecuencia de la
señal del dominio-tiempo original.

3. ( ) ( ) exp( )F f t i t dt 


 

1
( ) ( ) exp( )
2
f t F i t d  





La transformada
de
Fourier

4. Es decir,
donde:
Estas expresiones nos permiten calcular la
expresión F() (dominio de la frecuencia) a partir
de f(t) (dominio del tiempo) y viceversa.



  
 deFtf ti
)()( 2
1




 dtetfF ti
 )()(
Identidad
de Fourier
o antitrans-
formada de
Fourier
Transformada
de Fourier

5. ( ) ( ) exp( )F f t i t dt 


 

1
( ) ( ) exp( )
2
f t F i t d  






6. A la función F() se le llama transformada de
Fourier de f(t) y se denota por F o , es decir
En forma similar, a la expresión que nos
permite obtener f(t) a partir de F() se le llama
transformada inversa de Fourier y se denota
por F –1 ,es decir




  
 deFtfFF ti
)()()]([ 2
11




 dtetffFtfF ti
 )()(ˆ)()]([
fˆ

7. Transformadas integrales
–K(,t): núcleo o kernel.
–Asocia a cada función f(t) en el
espacio t, directo o real, otra función
F() en el espacio  o recíproco.
–Ejemplos: de Fourier, Wavelet,
transformada Z, de Laplace, de
Hilbert, de Radon, etc
dttftKF
b
a )(),()( 

8. Un problema que es difícil de resolver en sus
"coordenadas" (espacio t) originales, a menudo,
es más sencillo de resolver al transformarlo a
espacio .
Después, la transformada inversa nos devuelve la
solución en el espacio original.
Problem in
Transform space
Original
problem
Solution in
Transform space
Solution of
original problem
Integral transform
Relatively easy solution
Difficult solution
Inverse transform

9. Ejemplo. Calcular F() para el pulso
rectangular f(t) siguiente:
Solución. La expresión en el dominio del
tiempo de la función es:
9
-p/2
0 p/2
1
f(t)
t








 

t
t
t
tf
p
pp
p
2
22
2
0
1
0
)(

10. Integrando:
Usando la fórmula
de Euler:
i
ee
psen
pipi
2
)2/(
2/2/ 




 





2/
2/
)()(
p
p
titi
dtedtetfF 

2/
2/
1
p
p
ti
i e 

 
 )( 2/2/1 pipi
i ee 
  

)2/(sinc
2/
)2/(
)( pp
p
psen
pF 


 

11. En forma gráfica,
la transformada es:
-50 0 50
0
0.5
1
F(w) con p=1
w
F(w)
p =1








 

t
t
t
tf
p
pp
p
2
22
2
0
1
0
)(
)2/(sinc)( ppF  

12. Sinc(x/2) es la
transformada de
Fourier de una
función rectángulo.
Sinc2(x/2) es la
transformada de
Fourier de una
función triangulo.
Sinc2(ax) es el
patrón de difracción
de una ranura.
La función sinc(x)

13. Demostrar que la transformada de Fourier de la
función triángulo, D(t), es sinc2(/2)
0
2
sinc ( / 2)
1
t0
( )tD
1
1/2-1/2
TF

14. Ejercicio: Calcular la Transformada de Fourier
de la función escalón unitario o función de
Heaviside, u(t):
Grafica U() = F[u(t)].
¿Qué rango de frecuencias contiene U()?
¿Cuál es la frecuencia predominante?
u(t)
0
1
t

15. La función delta de Kronecker y delta de
Dirac
if 0
( )
0 if 0
t
t
t

 
 

t
(t)
,
1 if
0 if
m n
m n
m n


 


16. La función impulso o delta de Dirac
Recordemos que podemos pensar en la función delta como
el límite de una serie de funciones como la siguiente:
t
f1(t)
f2(t)
fm(t) = m exp[-(mt)2]/√
f3(t)
(t)

17. Y recordemos algunas propiedades de la
función 
( ) 1t dt



t
(t)
( ) ( ) ( ) ( ) ( )t a f t dt t a f a dt f a 
 
 
    
exp( ) 2 (
exp[ ( ) ] 2 (
i t dt
i t dt
   
     




  
     



18. Transformada de Fourier de la (t):
  )(ttf    1)(ˆ  



dtetf ti
 
t
(t)

1

()
Observa que la transformada de Fourier de
f(t) = 1/(2) es:
t
  )(dtefˆ ti
 



21
2
1
Recordemos

19. f t 
0 , t  
T
2
1 , 
T
2
 t 
T
2
0 ,
T
2
 t










T
2
T
2
T
2
T

2
T
2
2
)(ˆ
T
T
sen
Tf











20.  












2
,0
22
,1
2
,0
t
T
T
t
T
T
t
tf
2
2
)(ˆ
T
T
sen
Tf










f t  1
T ∞
  



 dtef ti
1ˆ 
 )( 2
T ∞

21. Transformada de Fourier de la función coseno
21
+000

0{cos( )}tFcos(0t)
t
0
  )cos( 0ttf    



 dtetf ti
 )cos(ˆ
0
  +




 +
 


+




dteedte
ee tititi
titi
)()( 00
00
2
1
2


 )()(
2
2
)(ˆ
00 

 ++f
 )()()(ˆ
00  ++f

22. Transformada de Fourier de la función seno:
  )( 0tsentf     



dtetsenf ti
 )(ˆ
0










 
 dte
i
ee ti
titi


2
00
 dtee
i
titi



+
 )()( 00
2
1 
 )()()(ˆ
00  + if
+0
00

sen(0t)
t
0
t)}sen({ 0F

23. La transformada de Fourier de la onda plana
exp(i0 t)
La TF de exp(i0t) es una frecuencia pura.
F {exp(i0t)}
0 0

exp(i0t)
0
t
tRe
Im
0
)(2
}{
0
)( 0
00












dte
dteeeF
ti
tititi

24. Sum
F {exp(i0t)}
0 0

exp(i0t)
0
t
tRe
Im
0
TF
0

TF

25. Encontrar la transformada de Fourier de la función:
 
0
0,0
0,








a
t
te
tf
at
   


0
ˆ dteef tiat 

2222
0
)(
0
)(
1
1
)10(
1










+

+



+

+

+


+

+
+

a
i
a
a
ia
ia
ia
iaia
ia
e
dte
tia
tia

26. La transformada de Fourier de una
Gaussiana, exp(-at2), es otra Gaussiana.
2 2
2
{exp( )} exp( )exp( )
exp( / 4 )
at at i t dt
a




   
 
F
t0
2
exp( )at
0
2
exp( / 4 )a
TF
.

27. La transformada inversa de Fourier
Dada la función en el espacio recíproco G(k), podemos
retornar al espacio directo mediante la inversa de la
transformada de Fourier:
  



 dkekGkGFxg ikx
)(
2
1
)()( 1
 



 dxexgkG ikx
)()(
  2
  2
)'(
)'(
)'(
''
2
1
)(
)()(
2
1
xg
xx
xxik
ikxikxikx
dxdkexg
dkedxexgdkekG
 
  


































28. A partir de su definición, obtener la transformada
inversa de Fourier de la función  
   33
3
5
3
2
+





ii
g
   
 
   
   
 
 
3ordendepolo3
3
)(
3
2
:residuos)de(teoríadeCálculo
3
5
3
2
3
5
3
2
3
31
1
33
33
1
1
21
iz
iz
e
zf
de
i
I
I
de
i
de
i
de
ii
gF
deggF
izx
xi
I
xi
I
xi
xi
xi





+









+

































  2  2

29.  
 
 
 
 
 
0x;0I
0x;ex
2
5
π2f(z)πi10I
2
eix
f(z)
3ordeni polo de3z
3iz
e
f(z)
dωe
3iω
5
I
):e residuos(teoría dICálculo de
0x;0I
0x;eπx2f(z)πi4I
2
eix
f(z)
2
x32
i3z
2
x32
i3z
3
izx
iωω
32
2
1
x32
i3-z
1
x32
i3-z
sRe
sRe
sRe
sRe





+

+















30.  






 

0x;ex5
0x;ex2
gF
:esFourierdeinversaadatransformlaLuego
x32
x32
1

31. 6136
1
)( 2




i
g



  
degxf xi
)()(
A partir de la definición, obtener la transformada inversa de Fourier de
la función:
Integrando en el plano complejo:
iziz
zzzz
zg
2
3
,
3
2
,
))((6
1
)( 21
21




32. • Si x > 0:

 



+

R
RR
k
k
izx
dwwGdzzG
zzGidzezg
)()(
)),((Res2)(
)(
2
1


izx
g(z)eG(z) Tomando
Haciendo lim R→∞ 



0
6136
1
lim)(limComo 2zz izz
zg

-R R
C

33. Jordan)de3(Lema0)(lim
)(R
  R
izx
dxezg

Entonces:











xx
k eezzGixf 3
2
2
3
5
2
)),((Res2)(


• Si x < 0:

 





R
RR
k
k
izx
dwwGdzzG
zzGidzezg
)()(
)),((Res2)(
)(
2
1



34. 
-R R
Haciendo lim R→∞






0
6136
1
lim
)(limComo
2z
z
izz
zg
Jordan)de3(Lema0)(lim
)(R
  R
izx
dxezg

Entonces: 0)),((Res2)(   kzzGixf 

















0, x0
0, xee
5
π2
f(x)
x
3
2
x
2
3

35. La condición de suficiencia para que la transformada de
Fourier de f(x), F() exista es:
es decir, que f(x) sea de cuadrado sumable. Funciones
que no vayan asintóticamente a cero cuando x tiende a
+ y – en general no tienen transformadas de Fourier.



dxxg
2
)(

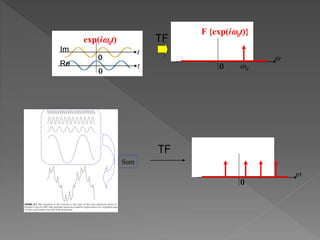
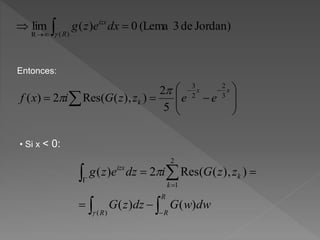
36. ( )exp( )
1
2 ( )exp( [ ] )
2
F t i t dt
F t i t dt

 






 


Si la TF de f(t) es F(), entonces la TF de F(t) es:
Renombrando la variable de integración de t a ’, podemos ver que
llegamos a la TF inversa:
1
2 ( )exp( [ ] )
2
F i d    



 
    
 

2 ( )f  
Este el motivo por el que a menudo f y F se dice que son
un "par transformado."
Que podemos escribir:

37. La transformada de Fourier es en general compleja
La transformada de Fourier F(k) y la función original f(x) son
ambas en general complejas.
De modo que la transformada de Fourier puede escribirse como:
  )()()( kiFkFxfF ir +
 
potenciadeespectroA
espectralfase
espectralmagnitudoamplitud
)(
)()()(
2222
22
)(
+


+
 
ir
ir
ki
FFF
A
FFkFA
ekAkFxfF

38. La transformada de Fourier cuando f(x) es real
La TF F(k) es particularmente simple cuando f(x) es real:
 















dx)kxsin()x(f)k(F
dx)kxcos()x(f)k(F
dx)kx(isen)kxcos()x(fdxe)x(f
i
r
ikx
  )k(iF)k(F)x(fF ir +

39. Propiedades de las transformadas de Fourier:
1. Linealidad:
f (t) F.T.
  ˆf  
g(t) F.T.
  ˆg  




 f(t) + g(t) F.T.
  ˆf  + ˆg  
f (t) F.T.
  ˆf   (a + ib) f (t) F.T.
  (a + ib) ˆf  

40. )}({)}({
)}()({
tgbFtfaF
tbgtafF
+
+
f(t)
g(t)
t
t
t



F()
G()
f(t) + g(t)
F() + G()

41. Calcular la transformada de Fourier de la siguiente función:
f (t) 
0 , t 
a
2
1 ,
b
2
 t 
a
2
2 , t 
b
2









; a  b  0
La función f(t) se puede escribir también del siguiente modo:
f (t)  g(t) + h(t)
donde g(t) 
0 , t 
a
2
1 , t 
a
2






; h(t) 
0 , t 
b
2
1 , t 
b
2







42. Luego:
ˆf ()  ˆg() + ˆh()
2
b
2
b
sen
2
b
2
a
2
a
sen
2
a
)(fˆ






 

+






 



43. Calcular la transformada de Fourier de la siguiente función:
0
1
-a -b b a0

44. Tenemos que calcular la transformada de Fourier de la siguiente
función:
f t 
0, t  a
1,  a  t  b
0,  b  t  b
1, b  t  a
0, t  a









; h(t) 
0 , t  b
1 , t  b




g(t) 
0 , t  a
1 , t  a




f t  g(t)  h(t)

45. F.T.
  ˆg() 
2a
2
sen(a)
a
h(t) 
0 , t  b
1 , t  b




g(t) 
0 , t  a
1 , t  a




F.T.
  ˆh() 
2b
2
sen(b)
b
ˆf ()  ˆg() ˆh() 
2a
2
sen(a)
a

2b
2
sen(b)
b

46.    )(ˆ ftfF 
  





















a
f
a
dtetf
a
atdeatf
a
dteatfatfF
t
a
i
at
a
i
ti



ˆ1
')'(
1
)()(
1
)(
'
)(
2. Escalado:    






a
f
a
atfF
ˆ1

47. Efecto de
la propiedad de
escalado
f(t) F()
Pulso
corto
Pulso
medio
Pulso
largo
Mientras más
corto es el
pulso, más
ancho es el
espectro.
Esta es la esencia
del principio de
incertidumbre en
mecánica cuántica.



t
t
t

48. La transformada de Fourier respecto al espacio
Si f(x) es función de la posición,
k se conoce como frecuencia
espacial.
Todo lo expuesto sobre la
transformada de Fourier entre los
dominios t y  se aplica los
dominios x y k.
k
x   )(ˆ)( kfdxexfxfF ikt
 




49. 3. Traslación en el dominio de tiempos
    
featfftf aiTFTF ˆ)(ˆ)( ....
 + 
  



 dtetgg ti
 )(ˆ 



+ dteatf ti
)(
  



 dueufg aui )(
)(ˆ 
 



 dueufe
uiai 
)(
  )(ˆˆ  
feg ai

f (t + a) g(t)

50. 4. : f (t)  f *
(t)  ˆf   ˆf *
 
   
   






)(ˆIm)(ˆIm
)(ˆRe)(ˆRe


ff
ff
5. :   


 dttff )(0ˆ
  


 

dff )(ˆ
2
1
0

51. 5. Identidad de Parseval : f *
(t)g(t)dt


  ˆf *
() ˆg()d



















 







dtdgdf ee
titi
'
'
)'(ˆ)(ˆ*


 















 edtgdfd
ti '
)'(ˆ')(ˆ )(* 

(' )
f (t)  g(t)  f(t)
2
dt


  ˆf ()
2
d



Teorema de Rayleigh



  dgf )(ˆ)(ˆ*
En particular:

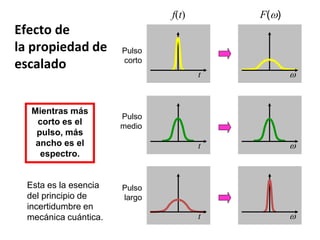
52. Toda función puede escribirse como la suma de una
función par y una función impar
( ) [ ( ) ( )]/ 2
( ) [ ( ) ( )]/ 2
( ) ( ) ( )
E x f x f x
O x f x f x
f x E x O x
 + 
  

 +
E(-x) = E(x)
O(-x) = -O(x)
E(x)
f(x)
O(x)
Sea f(x) una función cualquiera.

53. Transformadas de Fourier de funciones pares, f(t) = f(-t):
  



 dttff e
ti
 )(ˆ 





+  


0
0
)()( dttfdttf ee
titi 






+  
 

0 0
)()()(ˆ dttfdttff ee
titi 
  


+
0
)( dttf ee
titi 
  


0
)cos()(2ˆ dtttff 

54. 





+  
 

0 0
)()()(ˆ dttfdttff ee
titi 

Transformadas de Fourier de funciones impares, f(t) = -f(-t):
  



 dttff e
ti
 )(ˆ 





+  


0
0
)()( dttfdttf ee
titi 
 


+
0
)( dttf ee
titi 
  


0
)()(2ˆ dttsentfif 

55. 6. Transformada de la derivada:
ikF(k)ikF(f(x))(x))fF( 
  )k´(iF))x(f´(iF)x(xfF 
7. Transformada xf(x):
Y en general:
  F(k)ik(x))F(f
n)n(

Y en general:
  )k´(Fi)x(fxF nn


56. 1. Encontrar la transformada de Fourier de la
función:
2. A partir del resultado anterior y una conocida
propiedad de la transformada de Fourier, determina
la transformada de Fourier de la función:
 2
1
1
)(
x
xf
+

 22
1 x
x
)x(g
+

iz-izzf
z
zfdz
z
e
I
dx
x
e
kF
ikz
ikx

+

+

+









21
22
2
yexceptoC,zanalíticaes)(
1
1
)(con3"tipo"integral
1
:complejoplanoalintegrallaPasamos
1
)(integrallapidenNos1.

57. k
k
ikz
iz
ikz
iz
k
ikz
iz
ikz
iz
ekF
e
iz
e
i
z
e
ikF
e
iz
e
i
z
e
ikF
lím
lím

















+






+















+





)(:quemodoDe
2
1
2)(
:Ccircuitoelenintegramos0kPara
2
1
2)(
:Ccircuitoelenintegramos0kPara
2
1
2
2
Res
Res
C1
C2
 
 
   
  21
)(
1
2
1
2
:
1
2
yquePuesto
22
2222
22
k
k
eik
x
x
FkG
eik
x
x
F
x
x
F
x
x
dx
df
fikF
dx
df
F











+










+









+

+









2.

58. Encontrar la transformada de Fourier de la función:
siendo a>0 constante.







2
exp)(
2
ax
xf
)(
2
exp)(
2
exp)(
22
xaxf
ax
axxf
ax
xf 












)´()( kiaFkikF 
Derivando tenemos:
 






)´())(´()(
)())(())((
kiFxfiFxxfF
kikFxfikFxfF
Transformando a ambos lados de la ecuación y usando las siguientes
propiedades de la TF:
Veamos otra aplicación de estas dos últimas propiedades:

59. a
k
t
uu
ax
ikx
ax
a
k
e
a
kF
a
dt
t
e
a
due
a
due
a
dxeFB
dxeeBekF
2
0
0
2
22
2
22
2
22
2
)(
22
2
2
2
)0(
)(
























u2 = ax2/2
a
k
BekFkiaFkikF 2
2
)()´()(


u2 = t