1) La constante A debe ser 3 para que las señales φ1(t) y φ2(t) sean ortogonales. 2) El error cuadrático medio Ek en una aproximación de Fourier se reduce a medida que aumenta k. 3) La serie de Fourier de la función f(t)=1 para -π<t<0 y f(t)=0 para 0<t<π es 1/2 - ∞(−1)nsen(2n-1)t/(2n-1)2.

1. ´
UNIVERSIDAD TECNOLOGICA DE PEREIRA
´
FACULTAD DE INGENIERIAS
´ ´
PROGRAMA DE INGENIERIA ELECTRICA
´ ´ ˜
ANALISIS,TRANSMISION Y FILTRADO DE SENALES
´ ˜
Taller (2) sobre representacion de senales y transformadas de Fourier
˜
1. Determine la constante A para que las senales ϕ1 (t) ´
5. Encontrar la serie de Fourier para la funcion f (t)
y ϕ2 (t) sean ortogonales en el intervalo (−∞, ∞). definida por f (t) = t2 en el intervalo (−π, π) y
f (t + 2π) = f (t)
ϕ1 (t) = e−|t| ; ϕ1 (t) = 1 − Ae−2|t|
R// A = 3. f (t )
2. Demostrar que el error cuadr´ tico medio Ek en
a
´
una aproximacion a f (t) por Sk (t), donde Sk (t) es
´
una aproximacion en una serie finita de Fourier, se -2π -π π 2π t
reduce a:
∞
1 2 (−1)n
R// 3π +4 n2
cos(nt)
T n=1
2 k
1 2 1
Ek = |f (t)| dt − a2 −
0 (a2 + b2 )
T 2 n=1 n n ´
6. Encontrar la serie de Fourier de la funcion f (t)
−T
2 definida por f (t) = et en el intervalo (−π, π) y
f (t + 2π) = f (t)
´
3. Encontrar la serie de Fourier para la funcion f (t)
definida por f (t) = 1 para −π < t < 0, f (t) = 0,
para 0 < t < π y f (t + 2π) = f (t) f (t )
f (t )
-2π -π π 2π
t
t ∞
-2π 2senh(π) (−1)n
-π π 2π R// 1
+ (cos(nt) − n sen(nt))
π 2 1+n2
n=1
´
7. Aproximar la funcion f (t) = t en el intervalo (−π, π)
mediante una serie finita de Fourier de 5 t´ rminos
e
1 2
∞
sen(2n−1)t
que sean diferentes de cero. Calcular tambi´ n ele
R// −
2 π
n=1
2n−1
´
error cuadr´ tico medio en la aproximacion.
a
´
4. Encontrar la serie de Fourier de la funcion f (t) 5
(−1)n−1
R// 2 sen(nt), E5 = 0,363
definida por f (t) = t para el intervalo (−π, π) y n=1
n
f (t + 2π) = f (t)
8. Desarrollar f (t) = sen5 (t) en serie de Fourier.
f (t )
9. Demostrar que:
∞
1 1 1 1 π2
=1+ + + + ... =
-2π -π π 2π
t
n=1
n2 4 9 16 6
(Sugerencia: Hacer t = π en el resultado del problema 5)
R// 2
∞
(−1)n−1
sen(nt)
´
10. Determinar la representacion en serie exponencial
n
n=1 ˜
de Fourier para la senal x(t) que se ilustra.

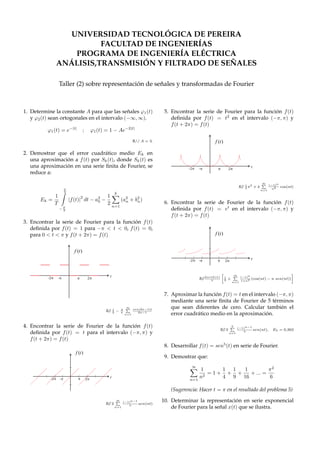
2. x(t)
d) cos ω0 t ↔ π[δ(ω − ω0 ) + δ(ω + ω0 )] 2
1
e) j sen ω0 t ↔ π[δ(ω − ω0 ) − δ(ω + ω0 )]
|t|
-4π -2π 0 2π 4π t 1− , |t| < τ ωτ 2
f) τ ↔ τ Sa 2
0 , |t| > τ
2 2 √ 2 2
˜ ´
11. Considerando la senal periodica cuadrada x(t) g) e−t /2σ ↔ σ 2πe−σ ω /2
como se ilustra en la figura.
´
17. Encontrar la transformada de Fourier de la funcion
X(t)
Signo, sgn(t), definida como:
A
1, t > 0
sgn(t) =
−1, t < 0
-2To -To -To/2 0 To/2 To 2To
t
2
R// sgn(t) ↔ jω
a) Determinar la serie exponencial compleja de
˜
Fourier de la senal x(t). Con la transformada anterior, verificar que la
b) Determinar la serie trigonom´ trica de Fourier
e ´
transfomada de Fourier de la funcion Escalon
´
˜
de la senal x(t). Unitario, u(t), est´ dada como:
a
c) Determinar la serie trigonom´ trica de Fourier
e 1
˜
de la senal y(t), cuando: u(t) ↔ πδ(ω) +
jω
A ´
18. Usando el teorema de la convolucion en el tiempo,
y(t) = x(t) −
2 encontrar la transformada inversa de Fourier de
d) Determinar la serie trigonom´ trica de Fourier
e
1
˜
de la senal y(t),cuando: X(ω) =
(a + jω)2
T0 A
y(t) = x t + − R// te−at u(t) ↔ 1
4 2 (a+jω)2
´
12. Dada la funcion ˜
19. Empleando el teorema de Parseval para senales de
Energ´a, evaluar la siguiente integral:
ı
0 para 0 < t < π
2
f (t) =
1 para π < t < π
2 ∞
dx
Desarrollar f (t) en una serie en t´ rminos del coseno
e −∞ a 2 + x2
´ ´
y trace la correspondiente extension periodica para π
R//
f (t) a
´
13. Dada la funcion ˜
Nota: El teorema de Parseval para senales de energ´a ı
2k l ´ ı ˜
establece una relacion entre la energ´a de la senal en
f (t) = l t para 0 < t < 2 el dominio del tiempo y la energ´a de la misma en el
ı
2k
l (l − t) para π < t < π
2 dominio de la frecuencia y est´ dada como:
a
Desarrollar f (t) en t´ rminos del seno y realizar la
e ∞ ∞
2 1 2
´ ´
correspondiente extension periodica. Ex = |x(t)| dt = |x(ω)| dω
−∞ 2π −∞
14. Encuentre la serie de Fourier en su segunda forma
para los ejercicios 3, 4, 5 y 6.
15. Demostrar cada una de las propiedades de la
transformada de Fourier.
16. Verificar cada una de las transformadas de Fourier
´
(integral de representacion) de las siguientes
˜ ´
senales. Bosquejar su representacion tanto en el
dominio del tiempo como en el dominio de la
frecuencia.
a) 1 ↔ 2πδ(ω)
b) ejω0 t ↔ 2πδ(ω − ω0 )
c) e−jω0 t ↔ 2πδ(ω + ω0 )