Derivadas parciales

FACULTAD DE CIENCIAS E
INGENIERÍA
E.A.P. de: INGENIERÍA ELÉCTRONICA CON
MENCIÓN EN TELECOMUNICACIONES
MATEMÁTICA APLICADA A LA INGENIERÍA III CICLO: III
Lic.: Miguel Ángel Tarazona Giraldo E_MAIL. mtarazona@uch.edu.pe
Web: http://jacobiperu.com/ E_MAIL. mitagi@gmail.com 999685938
Página 1 de 12
TEMA: Derivadas parciales SEMANA: 08
TURNO: MAÑANA PABELLÓN: B AULA: 604 SEMESTETRE: 2017 - I
Derivadas parciales
DEFINICIÓN DE DERIVADAS PARCIALES DE UNA FUNCIÓN DE DOS VARIABLES
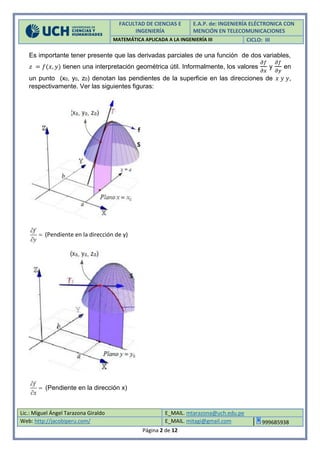
Si 𝑧 = 𝑓(𝑥, 𝑦), las primeras derivadas parciales de f con respecto a 𝒙 𝑦 𝒚
son las funciones fx y fy definidas por
𝜕
𝜕𝑥
𝑓(𝑥, 𝑦) = 𝑧 𝑥 =
𝜕𝑧
𝜕𝑥
= 𝑓𝑥(𝑥, 𝑦) = lim
∆𝑥→0
𝑓(𝑥 + ∆𝑥, 𝑦) − 𝑓(𝑥,𝑦)
∆𝑥
𝜕
𝜕𝑦
𝑓(𝑥, 𝑦) = 𝑧 𝑦 =
𝜕𝑧
𝜕𝑦
= 𝑓𝑦(𝑥, 𝑦) = lim
∆𝑦→0
𝑓(𝑥, 𝑦 + ∆𝑦) − 𝑓(𝑥,𝑦)
∆𝑦
Para hallar fx se considera y constante y se deriva con respecto a x. De manera similar, para
calcular fy, se considera x constante y se deriva con respecto a y.
DEFINICIÓN DE DERIVADAS PARCIALES DE UNA FUNCIÓN DE TRES VARIABLES
Si 𝑤 = 𝑓(𝑥, 𝑦, 𝑧), las primeras derivadas parciales de f con respecto a 𝒙, 𝒚 𝑦 𝒛 son las
funciones fx, fy y fz definidas por
𝜕
𝜕𝑥
𝑓(𝑥, 𝑦, 𝑧) = 𝑤𝑥 =
𝜕𝑤
𝜕𝑥
= 𝑓𝑥(𝑥, 𝑦, 𝑧) = lim
∆𝑥→0
𝑓(𝑥 + ∆𝑥, 𝑦, 𝑧) − 𝑓(𝑥,𝑦,𝑧)
∆𝑥
𝜕
𝜕𝑦
𝑓(𝑥, 𝑦, 𝑧) = 𝑤 𝑦 =
𝜕𝑤
𝜕𝑦
= 𝑓𝑦(𝑥, 𝑦, 𝑧) = lim
∆𝑦→0
𝑓(𝑥, 𝑦 + ∆𝑦, 𝑧) − 𝑓(𝑥,𝑦,𝑧)
∆𝑦
𝜕
𝜕𝑧
𝑓(𝑥, 𝑦, 𝑧) = 𝑤𝑧 =
𝜕𝑤
𝜕𝑧
= 𝑓𝑧(𝑥, 𝑦, 𝑧) = lim
∆𝑧→0
𝑓(𝑥, 𝑦, 𝑧 + ∆) − 𝑓(𝑥,𝑦,𝑧)
∆𝑧
Para hallar la derivada parcial con respecto a una de las variables, se mantienen constantes
las otras variables y se deriva con respecto a la variable dada.

INGENIERÍA
Página 2 de 12
Es importante tener presente que las derivadas parciales de una función de dos variables,
𝑧 = 𝑓(𝑥, 𝑦) tienen una interpretación geométrica útil. Informalmente, los valores
𝜕𝑓
𝜕𝑥
y
𝜕𝑓
𝜕𝑦
en
un punto (x0, y0, z0) denotan las pendientes de la superficie en las direcciones de 𝑥 𝑦 𝑦,
respectivamente. Ver las siguientes figuras:
f
y



(Pendiente en la dirección de y)
f
x



(Pendiente en la dirección x)

INGENIERÍA
Página 3 de 12
DERIVADAS PARCIALES DE ORDEN SUPERIOR
Como sucede en las derivadas ordinarias, es posible hallar las segundas, terceras, etc.
Derivadas parciales de una función de varias variables. Por ejemplo:
1) Derivar dos veces con respecto a x:
𝒇 𝒙𝒙 =
𝝏 𝟐 𝒇
𝝏𝒙 𝟐
=
𝝏
𝝏𝒙
(
𝝏𝒇
𝝏𝒙
)
2) Derivar dos veces con respecto a y:
𝒇 𝒚𝒚 =
𝝏 𝟐 𝒇
𝝏𝒚 𝟐 =
𝝏
𝝏𝒚
(
𝝏𝒇
𝝏𝒚
)
3) Derivar primero con respecto a x y luego con respecto a y:
𝒇 𝒙𝒚 =
𝝏 𝟐 𝒇
𝝏𝒚𝝏𝒙
=
𝝏
𝝏𝒚
(
𝝏𝒇
𝝏𝒙
)
4) Derivar primero con respecto a y y luego con respecto a x:
𝒇 𝒚𝒙 =
𝝏 𝟐 𝒇
𝝏𝒙𝝏𝒚
=
𝝏
𝝏𝒙
(
𝝏𝒇
𝝏𝒚
)
Los casos tercero y cuarto se llaman derivadas parciales mixtas.
IGUALDAD DE LAS DERIVADAS PARCIALES MIXTAS
Si f es una función de x y y y tal que fxy y fyx son continuas, entonces, para todo (𝑥, 𝑦)
fxy(x,y) = fyx(x,y)
Ejemplo 1.- Aplique la definición de derivada parcial para calcular 𝑓𝑋(𝑥, 𝑦) 𝑦 𝑓𝑌(𝑥, 𝑦) si:
𝑓(𝑥, 𝑦) = 3𝑥2
– 2𝑥𝑦 + 𝑦2
Solución
𝑓𝑥(𝑥, 𝑦) = lim
∆𝑥→0
𝑓(𝑥 + ∆𝑥, 𝑦)−𝑓(𝑥,𝑦)
∆𝑥
= lim
∆𝑥→0
3(𝑥+ ∆𝑥)2−2(𝑥+ ∆𝑥)𝑦 + 𝑦2− (3𝑥2− 2𝑥𝑦 + 𝑦2)
∆𝑥
= lim
∆𝑥→0
3(𝑥2+ 2𝑥.∆𝑥 + (∆𝑥)2) −2𝑥𝑦−2.∆𝑥.𝑦+𝑦2−3𝑥2+2𝑥𝑦−𝑦2
∆𝑥
=
= lim
∆𝑥→0
6𝑥(∆𝑥) + 3(∆𝑥)2 – 2(∆𝑥)𝑦
∆𝑥
= lim
∆𝑥→0
∆𝑥[6𝑥 + 3(∆𝑥) − 2𝑦]
∆𝑥
= 6𝑥 + 3(0) − 2𝑦 =
= 𝟔𝒙 − 𝟐𝒚

INGENIERÍA
Página 4 de 12
𝑓𝑦(𝑥, 𝑦) = lim
∆𝑦→0
𝑓(𝑥, 𝑦 + ∆𝑦) − 𝑓(𝑥, 𝑦)
∆𝑦
= lim
∆𝑦→0
3𝑥2
− 2𝑥(𝑦 + ∆𝑦) + (𝑦 + ∆y)2
− (3𝑥2
− 2𝑥𝑦 + 𝑦2)
∆𝑦
=
= lim
∆𝑦→0
3𝑥2
− 2𝑥𝑦 − 2(∆𝑦)𝑥 + 𝑦2
+ 2𝑦(∆𝑦) + (∆𝑦)2
− 3𝑥2
+ 2𝑥𝑦 − 𝑦2
∆𝑦
= lim
∆𝑦→0
∆𝑦[−2𝑥 + 2𝑦 + ∆𝑦]
∆𝑦
= −2𝑥 + 2𝑦 + 0 = −𝟐𝒙 + 𝟐𝒚
Ejemplo 2. Hallar las derivadas parciales fx y fy de la función f(x,y) = 3x - x2y2 + 2x3y.
Solución
∎ f(x,y) = 3x - x2y2 + 2x3y
fx(x,y) = 3 - 2xy2 + 6x2y
∎ f(x,y) = 3x - x2y2 + 2x3y
fy(x,y) = -2x2y + 2x3
Ejemplo 3. Dada f(x,y) = 𝑥𝑒 𝑥2 𝑦
, hallar fx y fy, y evaluar cada una en el punto (1,ln2).
Solución
∎ f(x,y) = 𝑥𝑒 𝑥2 𝑦
fx(x,y) = 𝑥. 𝑒 𝑥2 𝑦
. 2𝑥𝑦 + 𝑒 𝑥2 𝑦
= 𝑒 𝑥2 𝑦[2𝑥𝑦 + 1]
fx(1,ln2) = 𝑒(1)2 𝑙𝑛2[2(1)𝑙𝑛2 + 1] = 2[2𝑙𝑛2 + 1] = 4𝑙𝑛2 + 2
∎ f(x,y) = 𝑥𝑒 𝑥2 𝑦
fy(x,y) = 𝑥. 𝑒 𝑥2 𝑦
. 𝑥2
= 𝑥3
. 𝑒 𝑥2 𝑦
fy(1,ln2) = (1)3
. 𝑒(1)2 𝑙𝑛2
= 𝑒 𝑙𝑛2
= 2
Ejemplo 4. Hallar las pendientes en las direcciones de x y de y de la superficie dada por
f(x,y) = -
𝑥2
2
− 𝑦2
+
25
8
, en el punto (1/2,1,2).
Solución
∎ 𝑓(𝑥, 𝑦) = −
𝑥2
2
− 𝑦2 +
25
8
𝑓𝑥(𝑥, 𝑦) = −𝑥

INGENIERÍA
Página 5 de 12
Pendiente en la dirección de x es:
𝑓𝑥(
1
2
, 1) = −
1
2
∎ 𝑓(𝑥, 𝑦) = −
𝑥2
2
− 𝑦2 +
25
8
𝑓𝑦(𝑥, 𝑦) = −2𝑦
Pendiente en la dirección de y es:
𝑓𝑦(
1
2
, 1) = −2(1) = −2
Ejemplo 5. Hallar la derivada parcial de f(x,y,z) = xy + yz2 + xz con respecto a z.
Solución
fz(x,y,z) = 2yz +x
Ejemplo 6. Dada f(x,y,z) = z.sen(xy2 + 2z), hallar fz(x,y,z).
Solución
fz(x,y,z) = z.cos(xy2 + 2z)[2] + sen(xy2 + 2z) = 2z. cos(xy2 + 2z) + sen(xy2 + 2z)
Ejemplo 7. Dada f(x,y,z,w) =
𝑥+𝑦+𝑧
𝑤2 , hallar fw(x,y,z,w).
Solución
fw(x,y,z,w) = −2
(𝑥+𝑦+𝑧)
𝑤3
Ejemplo 8. Dada f(x,y) = 3xy2 – 2y + 5x2y2, hallar fxx(x,y), fyy(x,y), fxy(x,y) y fyx(x,y).
Solución
∎ fx(x,y) = 3y2 + 10xy2
fxx = 10y2
∎ fy(x,y) = 6xy – 2 + 10x2y
fyy= 6x + 10x2

INGENIERÍA
Página 6 de 12
∎ fxy(x,y) = 6y + 20xy
∎ fyx(x,y) = 6y + 20xy
Ejemplo 9. Demostrar que fxz = fzx y fxzz = fzxz = fzzx para la función dada por:
f(x,y,z) = y𝑒 𝑥
+ 𝑥𝑙𝑛𝑧
Solución
∎ fx(x,y,z) = y.𝑒 𝑥
+ 𝑙𝑛𝑧
∎ fz(x,y,z) =
𝑥
𝑧
∎ fxz(x,y,z) =
1
𝑧
fxz(x,y,z) = fzx(x,y,z)
∎ fzx(x,y,z) =
1
𝑧
∎ fxzz(x,y,z) = −
1
𝑧2
∎ fzxz(x,y,z) = −
1
𝑧2
fxzz(x,y,z) = fzxz(x,y,z) = fzzx(x,y,z)
∎ fzzx(x,y,z) = −
1
𝑧2
EJERCICIOS PROPUESTOS
1) Encuentre fx(x,y) y fy(x,y) dadas:
a) z = 𝑙𝑛
𝑥 + 𝑦
𝑥 − 𝑦
b) z =
𝑥2
2𝑦
+
4𝑦2
𝑥
c) z = 𝑒 𝑦
. 𝑠𝑒𝑛𝑥𝑦
d) z =
𝑥𝑦
𝑥2 + 𝑦2

INGENIERÍA
Página 7 de 12
e) 𝑧 = 𝑠𝑒𝑛(3𝑥). 𝑐𝑜𝑠(3𝑦)
2) Empleando la definición de derivadas, calcule fx(x,y) y fy(x,y) dada:
𝑓(𝑥, 𝑦) = √ 𝑥 + 𝑦
3) Encuentre fx(x,y,z), fy(x,y,z) y fz(x,y,z), dada:
a) 𝑓(𝑥, 𝑦) = 𝑙𝑛√𝑥2 + 𝑦2 + 𝑧2 b) w =
3𝑥𝑧
𝑥 + 𝑦
4) Calcule las cuatro derivadas parciales de segundo orden. Observe que las derivadas
parciales mixtas de segundo orden son iguales
a) z = arctg
𝑦
𝑥
b) z = 2𝑥. 𝑒 𝑦
− 3𝑦. 𝑒−𝑦
REGLA DE LA CADENA
REGLA DE LA CADENA: UNA VARIABLE INDEPENDIENTE
Sea 𝑤 = 𝑓(𝑥, 𝑦), donde 𝑓 es una función derivable de 𝑥 𝑦 𝑦. Si 𝑥 = 𝑔(𝑡) y 𝑦 = ℎ(𝑡),
donde 𝑔 𝑦 ℎ son funciones derivables de 𝑡, entonces 𝑤 es una función diferenciable de
𝑡, 𝑦
𝒅𝒘
𝒅𝒕
=
𝝏𝒘
𝝏𝒙
.
𝒅𝒙
𝒅𝒕
+
𝝏𝒘
𝝏𝒚
.
𝒅𝒚
𝒅𝒕
w
𝜕𝑤
𝜕𝑥
𝜕𝑤
𝜕𝑦
x y
𝑑𝑥
𝑑𝑡
𝑑𝑦
𝑑𝑡
t t
Regla de la cadena: una variable dependiente w, es función de x y y, lasque a su vez son
funciones de t. Este diagrama representa la derivada de w con respecto a t.

INGENIERÍA
Página 8 de 12
Ejemplo 1. Hallar dw/dt cuando t = 0, aplicando la regla de la cadena, dada w = x2y – y2,
donde x = sent y y = et.
Solución
w
𝜕𝑤
𝜕𝑥
𝜕𝑤
𝜕𝑦
x y
𝑑𝑥
𝑑𝑡
𝑑𝑦
𝑑𝑡
t t
𝑑𝑤
𝑑𝑡
=
𝜕𝑤
𝜕𝑥
.
𝑑𝑥
𝑑𝑡
+
𝜕𝑤
𝜕𝑦
.
𝑑𝑦
𝑑𝑡
= 2𝑥𝑦. cos(𝑡) + (𝑥2
− 2𝑦)𝑒 𝑡
=
= 2. 𝑠𝑒𝑛(𝑡). 𝑒 𝑡
. cos(𝑡) + (𝑠𝑒𝑛2
𝑡 − 2. 𝑒 𝑡)𝑒 𝑡
=
= 2. 𝑒 𝑡
. 𝑠𝑒𝑛(𝑡). cos(𝑡) + 𝑒 𝑡
. 𝑠𝑒𝑛2(𝑡) − 2. 𝑒2𝑡
Cuando t = 0 →
𝑑𝑤
𝑑𝑡
= 2. 𝑒0
. 𝑠𝑒𝑛(0). cos(0) + 𝑒0
. 𝑠𝑒𝑛2(0) − 2. 𝑒2(0)
= −2
REGLA DE LA CADENA: DOS VARIABLES INDEPENDIENTES
Sea w = f(x,y), f es una función diferenciable de x y y. Si x = g(s,t) y y = h(s,t), son
tales que las derivadas parciales de primer orden
𝜕𝑥
𝜕𝑠
,
𝜕𝑥
𝜕𝑡
,
𝜕𝑦
𝜕𝑠
y
𝜕𝑦
𝜕𝑡
, existen, entonces
𝜕𝑤
𝜕𝑠
y
𝜕𝑤
𝜕𝑡
existen y están dadas por:
𝝏𝒘
𝝏𝒔
=
𝝏𝒘
𝝏𝒙
.
𝝏𝒙
𝝏𝒔
+
𝝏𝒘
𝝏𝒚
.
𝝏𝒚
𝝏𝒔
𝒚
𝝏𝒘
𝝏𝒕
=
𝝏𝒘
𝝏𝒙
.
𝝏𝒙
𝝏𝒕
+
𝝏𝒘
𝝏𝒚
.
𝝏𝒚
𝝏𝒕
w
𝜕𝑤
𝜕𝑥
𝜕𝑤
𝜕𝑦
x y
𝜕𝑥
𝜕𝑡
𝜕𝑥
𝜕𝑠
𝜕𝑦
𝜕𝑡
𝜕𝑦
𝜕𝑠
t s t s

INGENIERÍA
Página 9 de 12
Regla de la cadena: una variable dependiente w, es función de x y y las que a su vez son
funciones de s y t. Este diagrama representa la derivada de w con respecto a t y s.
Ejemplo 2. Encuentre
𝜕𝑤
𝜕𝑠
𝑦
𝜕𝑤
𝜕𝑡
, dada w = 2xy, x = s2 + t2 y y = s/t
Solución
w
𝜕𝑤
𝜕𝑥
𝜕𝑤
𝜕𝑦
x y
𝜕𝑥
𝜕𝑡
𝜕𝑥
𝜕𝑠
𝜕𝑦
𝜕𝑡
𝜕𝑦
𝜕𝑠
t s t s
𝜕𝑤
𝜕𝑠
=
𝜕𝑤
𝜕𝑥
.
𝜕𝑥
𝜕𝑠
+
𝜕𝑤
𝜕𝑦
.
𝜕𝑦
𝜕𝑠
𝜕𝑤
𝜕𝑡
=
𝜕𝑤
𝜕𝑥
.
𝜕𝑥
𝜕𝑡
+
𝜕𝑤
𝜕𝑦
.
𝜕𝑦
𝜕𝑡
𝜕𝑤
𝜕𝑠
= 2𝑦(2𝑠) + 2𝑥 (
1
𝑡
) = 2 (
𝑠
𝑡
) 2𝑠 + 2(𝑠2
+ 𝑡2) (−
𝑠
𝑡2
) = 4𝑠 −
2𝑠3+2𝑠𝑡2
𝑡2
=
6𝑠2 + 2𝑡2
𝑡
𝜕𝑤
𝜕𝑡
= 2𝑦(2𝑡) + 2𝑥 (−
𝑠
𝑡2
) = 2 (
𝑠
𝑡
) 2𝑡 + 2(𝑠2
+ 𝑡2) (−
𝑠
𝑡2
) = 4𝑠 −
2𝑠3
+ 2𝑠𝑡2
𝑡2
=
=
4𝑠𝑡2
− 2𝑠3
− 2𝑠𝑡2
𝑡2
=
2𝑠𝑡2
− 2𝑠3
𝑡2
La regla de la cadena puede extenderse a cualquier número de variables.
Ejemplo 3.- Dada 𝑤 = 𝑥𝑦 + 𝑦𝑧 + 𝑥𝑧, 𝑥 = 𝑠. 𝑐𝑜𝑠𝑡, 𝑦 = 𝑠. 𝑠𝑒𝑛𝑡 y 𝑧 = 𝑡, para 𝑠 = 1 𝑦
𝑡 = 2𝜋. Hallar
𝜕𝑤
𝜕𝑠
𝑦
𝜕𝑤
𝜕𝑡
.
Solución
w
𝜕𝑤
𝜕𝑥
𝜕𝑤
𝜕𝑦
𝜕𝑤
𝜕𝑧
x y z
𝜕𝑥
𝜕𝑠
𝜕𝑥
𝜕𝑡
𝜕𝑦
𝜕𝑠
𝜕𝑦
𝜕𝑡
𝑑𝑧
𝑑𝑡
s t s t t

INGENIERÍA
Página 10 de 12
∎
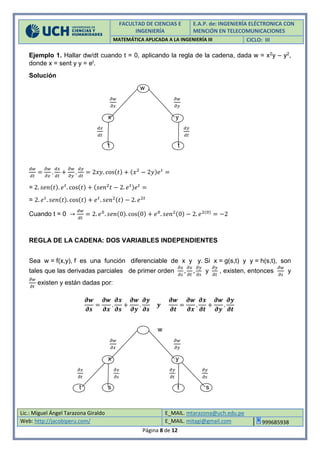
𝜕𝑤
𝜕𝑠
=
𝜕𝑤
𝜕𝑥
.
𝜕𝑥
𝜕𝑠
+
𝜕𝑤
𝜕𝑦
.
𝜕𝑦
𝜕𝑠
+
𝜕𝑤
𝜕𝑧
.
𝜕𝑧
𝜕𝑧
= (𝑦 + 𝑧)𝑐𝑜𝑠𝑡 + (𝑥 + 𝑧)𝑠𝑒𝑛𝑡 + (𝑦 + 𝑥). 0 =
= [𝑠. 𝑠𝑒𝑛𝑡 + 𝑡]𝑐𝑜𝑠𝑡 + [𝑠. 𝑐𝑜𝑠𝑡 + 𝑡]𝑠𝑒𝑛𝑡
Entonces, para 𝑠 = 1 𝑦 𝑡 = 2𝜋, tenemos que:
𝜕𝑤
𝜕𝑠
= [1. 𝑠𝑒𝑛2𝜋 + 2𝜋]𝑐𝑜𝑠2𝜋 + [1. 𝑐𝑜𝑠2𝜋 + 2𝜋]𝑠𝑒𝑛2𝜋 = 2𝜋
∎
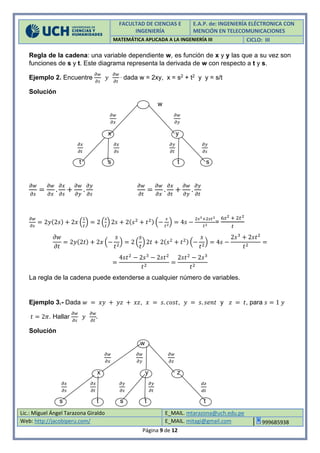
𝜕𝑤
𝜕𝑡
=
𝜕𝑤
𝜕𝑥
.
𝜕𝑥
𝜕𝑡
+
𝜕𝑤
𝜕𝑦
.
𝜕𝑦
𝜕𝑡
+
𝜕𝑤
𝜕𝑧
.
𝜕𝑧
𝜕𝑡
= −(𝑦 + 𝑧)𝑠. 𝑠𝑒𝑛𝑡 + (𝑥 + 𝑧)𝑠. 𝑐𝑜𝑠𝑡 + (𝑦 + 𝑥). 1 =
= −[𝑠. 𝑠𝑒𝑛𝑡 + 𝑡]𝑠. 𝑠𝑒𝑛𝑡 + [𝑠. 𝑐𝑜𝑠𝑡 + 𝑡]𝑠. 𝑐𝑜𝑠𝑡 + [𝑠. 𝑠𝑒𝑛𝑡 + 𝑠. 𝑐𝑜𝑠𝑡](1) =
= −[1. 𝑠𝑒2𝜋 + 2𝜋](1)𝑠𝑒𝑛2𝜋 + [(1)𝑐𝑜𝑠2𝜋 + 2𝜋](1)𝑐𝑜𝑠2𝜋 + [(1)𝑠𝑒𝑛2𝜋 + (1)𝑐𝑜𝑠2𝜋](1) =
= −[1. (0) + 2𝜋](1)(0) + [(1)(1) + 2𝜋](1)(1) + [(1). (0) + (1). (1)](1) = [1 + 2𝜋] + 1=
= 2 + 2𝜋
REGLA DE LA CADENA: DERIVACIÓN IMPLICITA
Si la ecuación F(x,y) = 0 define a y implícitamente como función derivable de x,
entonces:
𝒅𝒚
𝒅𝒙
= −
𝑭 𝒙(𝒙,𝒚)
𝑭 𝒚(𝒙,𝒚)
, 𝐹𝑦(𝑥, 𝑦) ≠ 0
Si la ecuación F(x,y,z) = 0 define a z implícitamente como una función dife-
renciable de x y y, entonces:
𝝏𝒛
𝝏𝒙
= −
𝑭 𝒙(𝒙, 𝒚, 𝒛)
𝑭 𝒛(𝒙, 𝒚, 𝒛)
𝒚
𝝏𝒛
𝝏𝒚
= −
𝑭 𝒚(𝒙, 𝒚, 𝒛)
𝑭 𝒛(𝒙, 𝒚, 𝒛)
, 𝑭 𝒛(𝒙, 𝒚, 𝒛) ≠ 𝟎
Ejemplo 4. Dada y3 + y2 – 5y – x2 + 4 = 0, hallar
𝑑𝑦
𝑑𝑥
.
Solución
Definiendo: F(x,y) = y3 + y2 – 5y – x2 + 4
Fx(x,y) = -2x
Fy(x,y) = 3y2 + 2y – 5

INGENIERÍA
Página 11 de 12
Luego:
𝑑𝑦
𝑑𝑥
= −
𝐹𝑥(𝑥,𝑦)
𝐹𝑦(𝑥,𝑦)
= −
(−2𝑥)
3𝑦2+ 2𝑦 − 5
=
2𝑥
3𝑦2+ 2𝑦 − 5
Ejemplo 5. Dada la ecuación: 3x2z – x2y2 + 2z3 + 3yz – 5 = 0, hallar
𝜕𝑧
𝜕𝑥
𝑦
𝜕𝑧
𝜕𝑦
.
Solución
Definiendo: F(x,y,z) = 3x2z – x2y2 + 2z3 + 3yz – 5
∎
𝜕𝑧
𝜕𝑥
= −
𝐹𝑥(𝑥,𝑦,𝑧)
𝐹𝑧(𝑥,𝑦,𝑧)
= −
6𝑥𝑧−2𝑥𝑦2
3𝑥2+ 6𝑧2+3𝑦
=
2𝑥𝑦2− 6𝑥𝑧
3𝑥2+ 6𝑧2+3𝑦
∎
𝜕𝑧
𝜕𝑦
= −
𝐹𝑦(𝑥,𝑦,𝑧)
𝐹𝑧(𝑥,𝑦,𝑧)
= −
−2𝑥2 𝑦 + 3𝑧
3𝑥2+ 6𝑧2 + 3𝑦
=
2𝑥2 𝑦 − 3𝑧
3𝑥2+ 6𝑧2 + 3𝑦
EJERCICIOS PROPUESTOS
1) Sean u = x2 + y3, x = r.es y y = r.e-s, aplicar la regla de la cadena para calcular
𝜕𝑢
𝜕𝑟
𝑦
𝜕𝑢
𝜕𝑠
.
Resp.
𝜕𝑢
𝜕𝑟
= 2𝑟. 𝑒2𝑠
+ 3𝑟2
𝑒−3𝑠
.
𝜕𝑢
𝜕𝑠
= 2𝑟2
𝑒2𝑠
− 3𝑟3
𝑒−3𝑠
.
2) Sean y = 2wz + z2, w = ex y z = cosx, calcule la derivada total
𝑑𝑦
𝑑𝑥
, aplicando la regla de
la cadena. Resp.
𝑑𝑦
𝑑𝑥
= 2𝑒 𝑥
. 𝑐𝑜𝑠𝑥 − 2𝑒 𝑥
. 𝑠𝑒𝑛𝑥 − 2𝑠𝑒𝑛𝑥. 𝑐𝑜𝑠𝑥
3) Sean u = x2+ yz, x = r.sent, y = r.cost y z = r.sen2t; calcule
𝜕𝑢
𝜕𝑟
𝑦
𝜕𝑢
𝜕𝑡
.
Resp.
𝜕𝑢
𝜕𝑟
= 2𝑟𝑠𝑒𝑛2
𝑡(1 + 𝑐𝑜𝑠𝑡).
𝜕𝑢
𝜕𝑡
= 𝑟2
. 𝑠𝑒𝑛𝑡(2𝑐𝑜𝑠𝑡 + 2𝑐𝑜𝑠2
𝑡 − 𝑠𝑒𝑛2
𝑡).
4) Calcule
𝑑𝑦
𝑑𝑥
, si 𝑥. 𝑐𝑜𝑠𝑦 + 𝑦. 𝑐𝑜𝑠𝑥 – 1 = 0. Resp.
𝑑𝑦
𝑑𝑥
= −
𝑦.𝑠𝑒𝑛𝑥 − 𝑐𝑜𝑠𝑦
𝑐𝑜𝑠𝑥−𝑥𝑠𝑒𝑛𝑦
.
5) Calcule
𝜕𝑧
𝜕𝑥
𝑦
𝜕𝑧
𝜕𝑦
si 4z3 + 3xz2 – xy2 – 2x2y + 7= 0.
Resp.
𝜕𝑧
𝜕𝑥
=
𝑦2+ 4𝑥𝑦− 3𝑧2
12𝑧2+ 6𝑥𝑧
.
𝜕𝑧
𝜕𝑦
=
𝑥𝑦 + 𝑥2
6𝑧2+ 3𝑥𝑧
6) Calcule
𝜕𝑢
𝜕𝑟
𝑦
𝜕𝑢
𝜕𝑡
si u = ey/r, x = 2r.cost y y = 4r.sent.
Resp.
𝜕𝑢
𝜕𝑟
=
2𝑒
𝑦
𝑥⁄
𝑥2
(2𝑥𝑠𝑒𝑛𝑡 − 𝑦𝑐𝑜𝑠𝑡);
𝜕𝑢
𝜕𝑡
=
2𝑟𝑒
𝑦
𝑥⁄
𝑥2
(𝑦𝑠𝑒𝑛𝑡 + 𝑒𝑥𝑐𝑜𝑠𝑡)

INGENIERÍA
Página 12 de 12
7) Calcule
𝜕𝑢
𝜕𝑟
𝑦
𝜕𝑢
𝜕𝑠
si 𝑢 = 𝑎𝑟𝑐𝑠𝑒𝑛(3𝑥 + 𝑦), x = r2.ex, 𝑦 = 𝑠𝑒𝑛(𝑟𝑠).
Resp.
𝜕𝑢
𝜕𝑟
=
6𝑟𝑒 𝑠− 𝑠.cos(𝑟𝑠)
√1−(3𝑥+𝑦)2
;
𝜕𝑢
𝜕𝑠
=
3𝑒2.𝑒 𝑠+ cos(𝑟𝑠)
√1−(3𝑥+𝑦)2
8) Calcule
𝜕𝑢
𝜕𝑟
,
𝜕𝑢
𝜕∅
𝑦
𝜕𝑢
𝜕𝜃
si u = x2 + y2 + z2, 𝑥 = 𝑟. 𝑠𝑒𝑛∅. 𝑐𝑜𝑠𝜃, 𝑦 = 𝑟. 𝑠𝑒𝑛∅. 𝑠𝑒𝑛𝜃 y
𝑧 = 𝑟. 𝑐𝑜𝑠∅.
Resp.
𝜕𝑢
𝜕𝑟
= 2𝑥𝑠𝑒𝑛∅cos𝜃 + 2ysen∅sen𝜃 + 2zcos∅
𝜕𝑢
𝜕∅
= 2𝑥𝑟𝑐𝑜𝑠∅cos𝜃 + 2y.rcos∅sen𝜃 - 2z.rsen∅
𝜕𝑢
𝜕𝜃
= −2𝑥. 𝑟sen∅.sen𝜃 + 2y.rsen∅cos𝜃
9) Calcule
𝜕𝑤
𝜕𝑠
𝑦
𝜕𝑤
𝜕𝑡
si 𝑤 = 𝑠𝑒𝑛(2𝑥 + 3𝑦), 𝑥 = 𝑠 + 𝑡 y 𝑦 = 𝑠 – 𝑡; evalúe para 𝑠 = 0,
t=
𝜋
2
.
10) Calcule aplicando la regla de la cadena la
𝜕𝑤
𝜕𝑢
𝑦
𝜕𝑤
𝜕𝑣
dada w = ln(x2+y2+z2),
x= u.ev.senu, y = u.ev.cosu, z = u.ev. Evaluar para (𝑢, 𝑣) = (−2,0).
BIBLIOGRAFÍA
Nakamura - Métodos numéricos aplicados con software
Hirsh - Numerical computation of internal and external flows. I
REFERENCIAS
https://www.google.com.pe/search?q=files%20upc%20cohortejun%202013%20webnode%20es%20MA
TEMATICA%20PARA%20INGENIE
https://urmate.jimdo.com/c%C3%A1lculo-integral/

Derivadas parciales

Más contenido relacionado

La actualidad más candente

Similar a Derivadas parciales

Más de UNI - UCH - UCV - UNMSM - UNFV

Último

Derivadas parciales