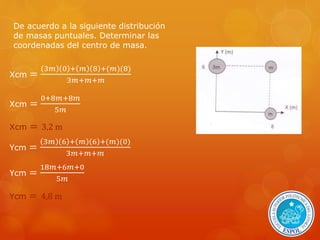
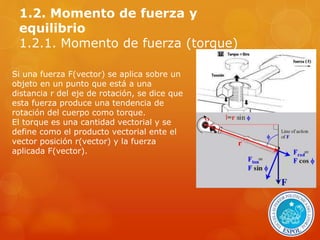
Este documento presenta una introducción al movimiento de cuerpos rígidos, incluyendo definiciones clave como cuerpos rígidos, centro de masa y eje de rotación. Explica que el centro de masa se mueve como una partícula en traslación, mientras que el cuerpo rota alrededor de su eje. También define el momento de fuerza (torque) como el producto vectorial entre la fuerza aplicada y la distancia al eje, y que es máximo cuando la fuerza es perpendicular a la línea de acción.

2. INDICE
1.1. Definiciones importantes
1.1.1. Cuerpos rígidos
1.1.2. Centro de Masa
1.1.3. Eje de rotación
1.2. Momento de fuerza y equilibrio
1.2.1. Momento de fuerza (torque)
1.2.2. Equilibrio
1.3. Dinámica rotacional
1.3.1. Segunda ley de Newton
1.3.2. Momento de inercia
1.3.3. Teorema de ejes paralelos
1.4. Trabajo rotacional y energía cinética
1.4.1. Teorema trabajo-energía y energía cinética
1.5. Cantidad de movimiento angular
1.5.1. Conservación de la cantidad de movimiento angular

3. INTRODUCCION
Hasta este momento hemos estudiado el
movimiento de una partícula en
traslación pura, el movimiento circular
uniforme y variado, pero
independientemente en este capitulo
estudiaremos el movimiento de
traslación de cuerpos rígidos, analizando
el movimiento de traslación de un punto
del cuerpo llamado centro de masa y la
rotación del cuerpo alrededor de un eje
de rotación, es decir, se estudiará el
movimiento de un cuerpo rígido en
rotación pura o también el movimiento
del cuerpo en traslación y rotación.

4. 1.1.1. Cuerpos rígidos
Un cuerpo rígido es aquel que permanece
sin deformación balo la aplicación de
fuerzas o torques externos sobre el
mismo, es decir, mantiene sus
dimensiones y su geometría invariables.
El cuerpo rígido es una idealización par
aestudiar y resolver problemas de
mecánica de una forma sencilla, pero en
la realidad todos los cuerpos sufren
variaciones en sus dimensiones cuando
son sometidos a fuerzas externas, dichas
variaciones serán estudiadas en el
capítulo de elasticidad.

5. 1.1.2. Centro de Masa
El centro de masa, es el punto donde
se considera concentrada toda la
materia (masa) del cuerpo o sistema
de particulas. Es decir, si se aplica
una fuerza resultante F(vector) sobre
el centro de masa, este cuerpo o el
sistema de partículas adquieren la
misma aceleración, que si la fuerza se
aplicara sobre ellos.
Si el cuerpo se mueve en traslación y
rotación el centro de masa se mueve
como si fuera una partícula. El centro
de masa puede estar dentro o fuera
del cuerpo.
Las coordenadas del centro de masa
están dadas por las siguientes
expresiones :

6. Donde x, y, z son las coordenadas del centro de
masa de cada partícula, con respecto a un sistema
de referencia y m la masa de cada partícula.
La ubicación del centro de masa para placas planas,
de igual espesor y material homogéneo está dada
por las siguientes expresiones :
Xcm=
푥1퐴1+푥2퐴2+ ………… +푀푛푋푛
퐴1+퐴2+ ……..+퐴푛
Ycm=
푦1퐴1+푦2퐴2+ ………… +푀푛푦푛
퐴1+퐴2+ ……..+퐴푛
Zcm=
푧1퐴1+푧2퐴2+ ………… +푀푛푍푛
퐴1+퐴2+ ……..+퐴푛

7. De acuerdo a la siguiente distribución
de masas puntuales. Determinar las
coordenadas del centro de masa.
Xcm =
3푚 0 + 푚 8 +(푚)(8)
3푚+푚+푚
Xcm =
0+8푚+8푚
5푚
Xcm = 3,2 m
Ycm =
3푚 6 + 푚 6 +(푚)(0)
3푚+푚+푚
Ycm =
18푚+6푚+0
5푚
Ycm = 4,8 m

8. De acuerdo a la figura mostrada por un
conjunto de placas homogéneas y de
espesor constante. Determinar el centro
de masa del sistema.
Xcm =
50 2,5 + 20 7,5 +(50)(12,5)
50+20+50
Xcm = 54,38 m
Ycm =
50 5 + 20 2 +(50)(5)
50+20+50
Ycm = 4,5 m

9. 1.1.3. Eje de rotación
Es una línea recta imaginaria perpendicular al
plano de rotación alrededor de la cual todos los
puntos describen trayectorias circulares. El eje de
rotación se puede colocar en cualquier parte del
cuerpo inclusive en el centro de masa.

10. 1.2. Momento de fuerza y
equilibrio
1.2.1. Momento de fuerza (torque)
Si una fuerza F(vector) se aplica sobre un
objeto en un punto que está a una
distancia r del eje de rotación, se dice que
esta fuerza produce una tendencia de
rotación del cuerpo como torque.
El torque es una cantidad vectorial y se
define como el producto vectorial ente el
vector posición r(vector) y la fuerza
aplicada F(vector).

11. Donde t(vector) es el torque y 휃 es el ángulo
comprendido entre el vector posición r(vector) y la
fuerza F(vector)
De acuerdo a la ecuación se puede observar que el
torque será máximo cuando el ángulo es 휃 =
90(grados centígrados) es decir cuando la fuerza y
el vector posición son perpendiculares
El torque será minimo, valor cero, cuando el ángulo
sea 휃 = 0 y 휃 = 180.

12.  Maneras de maximizar el torque :
* Aumentando la fuerza.
* Aumentando la magnitud del vector posición.
* Orientando la fuerza para que sea perpendicular al vector posición.
 Maneras de minimizar el torque :
* Disminuyendo la fuerza.
* Disminuyendo la magnitud del vector posición.
* Aplicando la fuerza paralela al vector posición.

13. Se deja aflojar un perno aplicando una fuerza de 100N de magnitud
en un punto cuyo vector posición es de magnitud 20 cm. La fuerza
forma un ángulo 휃 = 30(grados) con la dirección del vector posición
como se muestra en la figura
T(torque)= (r)(F)Sen(휃)
T(torque)= (0,2 mts)(100N)Sen(30)
T(torque)= 10(N)(mts)