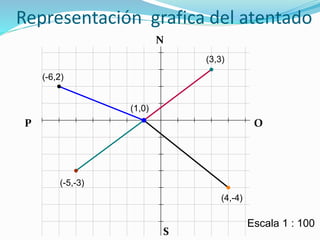
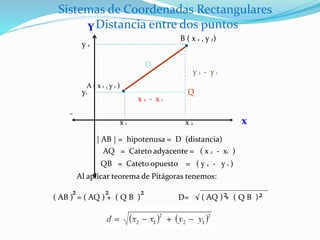
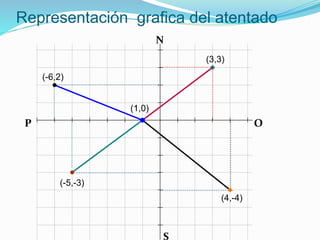
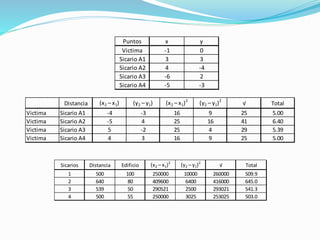
Este documento explica cómo calcular la distancia entre dos puntos usando coordenadas cartesianas. Define la distancia como la longitud del segmento que une dos puntos. Explica que para calcular la distancia se usa el Teorema de Pitágoras, donde la distancia es la raíz cuadrada de la suma de los cuadrados de la diferencia de las coordenadas x e y de los dos puntos. Luego, aplica esto para calcular la distancia entre el punto donde fue asesinado un hombre y los cuatro puntos donde se encontraron francotiradores para determinar quién

1. Unidad I
Sistemas de Ejes Coordenados
Tema 1.2
Distancia entre dos puntos

2. Objetivo del Tema:
Lo que se resolverá es un problema
teórico y práctico del sistema de ejes
coordenados, mediante la investigación de
gráficas en los que se representan
coordenadas cartesianas de un punto y
distancia entre dos puntos.

3. Distancia entre dos puntos
 Se define como la magnitud de la longitud
entre dos puntos cualesquiera.
 La magnitud debe entenderse como el
valor absoluto, ya que no existen
distancias negativas

4. Distancia entre dos puntos
En geometría se define la distancia entre
dos puntos como la longitud del
segmento de recta que une a estos dos
puntos.

5.  Homicidio en Tuxtla Gutiérrez, extra, extra!!!!!
En la mañana del viernes 11 de noviembre del 2011, un empresario de la
ciudad de Tuxtla Gutiérrez se disponía a trasladar 100 mil pesos del banco
ubicado en la 1pte y avenida central de esta ciudad a una de sus oficinas
para pagar a sus empleados, cuando el mencionado anteriormente se
disponía a cruzar la avenida central a las 11:00 hrs se escucho un disparo
con arma de fuego de alto calibre y largo alcance, teniendo como destino el
cuerpo del sujeto que se llamaba Juan Ismael Cacho.
Los servicios de emergencia del 066 se alertaron rápidamente para realizar
las averiguaciones previas y en este operativo se lograron capturar a 4
sicarios, el primero se localizo en la 3 Ote y 3 Nte dentro de un edificio a
una altura de 100 metros, el segundo se aprendió en la 4 Ote y 4 Sur
encontrándose a una altura de 80 metros, el tercero se capturo en la 6 Pte y
2 Nte a una altura de 50 metros y el ultimo se detuvo en la 5 Pte y 3 Sur
encontrándose a una altura de 55 mts.
Según el estudio de balística por su penetración y dirección del impacto en
el hoy occiso, se comprobó que recorrió la distancia aproximada de 539
metros. ¿Quién de los cuatro sicarios mato al individuo?
Nota: cada bloque de cuadras se aclara tomar como una distancia de 100 mts,
incluida la calle.
Se realizara la solución en el plano con (x, y)

6. X
Y
Cuadrantes
III
III IV
+
+
-
-
P ( X , Y )
Sistemas de Coordenadas Rectangulares
ABSCISAS
O
R
D
E
N
A
D
A
S
Estos ejes coordenados dividen el plano en cuatro regiones llamadas
cuadrantes, los cuales se ordenan en sentido contrario al giro de las
manecillas del reloj. Todo punto P del plano se localiza por medio del
sistema rectangular;
0

7. Representación grafica del atentado
(3,3)
(-6,2)
(-5,-3)
(4,-4)
(1,0)
Escala 1 : 100
N
OP
S

8. x
Y
-
A ( x 1 , y 1 )
Sistemas de Coordenadas Rectangulares
Distancia entre dos puntos
B ( x 2 , y 2)
x 1 x 2
y1
y 2
y 2 - y 1
x 2 - x 1
D
| AB | = hipotenusa = D (distancia)
Q
QB = Cateto opuesto = ( y 2 - y 1 )
AQ = Cateto adyacente = ( x 2 - x1 )
Al aplicar teorema de Pitágoras tenemos:
( AB ) = ( AQ ) + ( Q B ) D= √ ( AQ ) + ( Q B )
2 2 2 2 2

9. Representación grafica del atentado
(3,3)
(-6,2)
(-5,-3)
(1,0)
(4,-4)
N
S
OP

10. 
 D = √ ( x 2 - x1 )2 + ( y 2 - y 1 )2
D = √ ( -1 - 3 )2 + ( 0 - 3 )2 = √ 25 = 5.00
D = √ ( -1 - 4 )2 + ( 0 + 4 )2 = √41 = 6.40
D = √ ( -1 + 6 )2 + ( 0 - 2 )2 = √29 = 5.39
D = √ ( -1 + 5 )2 + ( 0 + 3 )2 = √25 = 5.00
Puntos x y
Victima -1 0
Sicario A1 3 3
Sicario A2 4 -4
Sicario A3 -6 2
Sicario A4 -5 -3

11. Puntos x y
Victima -1 0
Sicario A1 3 3
Sicario A2 4 -4
Sicario A3 -6 2
Sicario A4 -5 -3
Distancia (x2 – x1) (y2 – y1) (x2 – x1)2
(y2 – y1)2
√ Total
Victima Sicario A1 -4 -3 16 9 25 5.00
Victima Sicario A2 -5 4 25 16 41 6.40
Victima Sicario A3 5 -2 25 4 29 5.39
Victima Sicario A4 4 3 16 9 25 5.00
Sicarios Distancia Edificio (x2 – x1)2
(y2 – y1)2
√ Total
1 500 100 250000 10000 260000 509.9
2 640 80 409600 6400 416000 645.0
3 539 50 290521 2500 293021 541.3
4 500 55 250000 3025 253025 503.0

13. Conceptos clave
 Abscisa
 Cuadrante
 Distancia entre dos puntos
 Ordenada
 Par ordenado
 Raíz cuadrada
 Teorema de Pitágoras
 Sistema de coordenadas Rectangulares
(Plano Cartesiano)