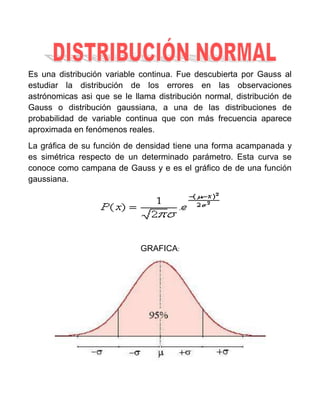
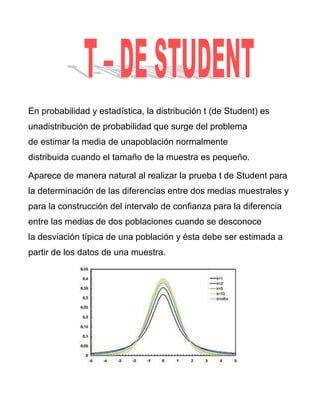
El documento describe varias distribuciones de probabilidad importantes como la distribución de Bernoulli, binomial, Poisson, normal, gamma y t de Student. Explica sus características clave y cómo se utilizan para modelar diferentes tipos de fenómenos aleatorios.

1. UNIVERSIDAD TECONOLOGICO DE TORREÓN
PROCESOS INDUSTRIALES
KAREM LUCERO GARCÍA VITELA 2°B

2. En teoría de
probabilidad y estadística,
la distribución de Bernoulli (o
distribución dicotómica), nombrada
así por
el matemático y científico suizo Jako
b Bernoulli, es una distribución de probabilidad discreta, que toma
valor 1 para la probabilidad de éxito ( ) y valor 0 para la probabilidad
de fracaso ( ).
Si es una variable aleatoria que mide "número de éxitos", y se
realiza un único experimento con dos posibles resultados (éxito o
fracaso), se dice que la variable aleatoria se distribuye como una
Bernoulli de parámetro .
Un experimento de Bernoulli es el lanzamiento de una moneda con
probabilidad p para cara y (1-p) para cruz.

3. En estadística, la distribución binomial es una distribución de
probabilidad discreta que mide el número de éxitos en una secuencia
de n ensayos de Bernoulli independientes entre sí, con una
probabilidad fija p de ocurrencia del éxito entre los ensayos.
Un experimento de Bernoulli se caracteriza por ser dicotómico, esto
es, sólo son posibles dos resultados. A uno de estos se denomina
éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con
una probabilidad q = 1 - p. En la distribución binomial el anterior
experimento se repite n veces, de forma independiente, y se trata de
calcular la probabilidad de un determinado número de éxitos. Para n =
1, la binomial se convierte, de hecho, en una distribución de Bernoulli.
Para representar que una variable aleatoria X sigue una distribución
binomial de parámetros n y p, se escribe:

4. La distribución de Poisson se llama así
en honor a su creador, el francés
Simeón Dennis Poisson (1781-1840).
Esta distribución de probabilidades fue
uno de los múltiples trabajos
matemáticos que Dennis completó en
su productiva trayectoria.
La distribución de Poisson se utiliza en situaciones donde los
sucesos son impredecibles o de ocurrencia aleatoria. En otras
palabras no se sabe el total de posibles resultados.
Permite determinar la probabilidad de ocurrencia de un suceso
con resultado discreto.
Es muy útil cuando la muestra o segmento n es grande y la
probabilidad de éxitos p es pequeña.
Se utiliza cuando la probabilidad del evento que nos interesa se
distribuye dentro de un segmento n dado como por ejemplo
distancia, área, volumen o tiempo definido.

5. Es una distribución variable continua. Fue descubierta por Gauss al
estudiar la distribución de los errores en las observaciones
astrónomicas asi que se le llama distribución normal, distribución de
Gauss o distribución gaussiana, a una de las distribuciones de
probabilidad de variable continua que con más frecuencia aparece
aproximada en fenómenos reales.
La gráfica de su función de densidad tiene una forma acampanada y
es simétrica respecto de un determinado parámetro. Esta curva se
conoce como campana de Gauss y e es el gráfico de de una función
gaussiana.
GRAFICA:

6. En estadística la distribución gamma es una distribución de
probabilidad continua con dos parámetros y cuya función de
densidad para valores es
Los parámetros de la distribución
El primer parámetro (α) situa la máxima intensidad de probabilidad y
por este motivo en algunas fuentes se denomina “la forma” de la
distribución: cuando se toman valores próximos a cero aparece
entonces un dibujo muy similar al de la distribución exponencial.
Cuando se toman valores más grandes de (α) el centro de la
distribución se desplaza a la derecha y va apareciendo la forma de
una campana de Gauss con asimetría positiva. Es el segundo
parámetro (β) el que determina la forma o alcance de esta asimetría
positiva desplazando la densidad de probabilidad en la cola de la
derecha. Para valores elevados de (β) la distribución acumula más
densidad de probabilidad en el extremo derecho de la cola, alargando
mucho su dibujo y dispersando la probabilidad a lo largo del plano. Al
dispersar la probabilidad la altura máxima de densidad de probabilidad
se va reduciendo; de aquí que se le denomine “escala”. Valores más
pequeños de (β) conducen a una figura más simétrica y concentrada,
con un pico de densidad de probabilidad más elevado. Una forma de
interpretar (β) es “tiempo promedio entre ocurrencia de un suceso”.
Relacionándose con el parámetro de la Poisson como β=1/λ.
Alternativamente λ será el ratio de ocurrencia: λ=1/β. La expresión
también será necesaria más adelante para poder llevar a cabo el
desarrollo matemático.

7. En probabilidad y estadística, la distribución t (de Student) es
unadistribución de probabilidad que surge del problema
de estimar la media de unapoblación normalmente
distribuida cuando el tamaño de la muestra es pequeño.
Aparece de manera natural al realizar la prueba t de Student para
la determinación de las diferencias entre dos medias muestrales y
para la construcción del intervalo de confianza para la diferencia
entre las medias de dos poblaciones cuando se desconoce
la desviación típica de una población y ésta debe ser estimada a
partir de los datos de una muestra.