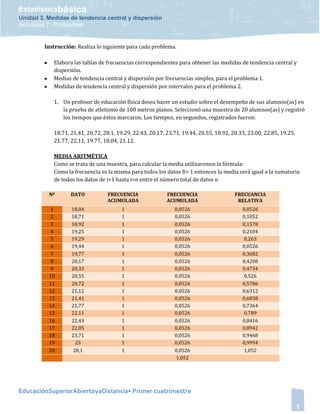
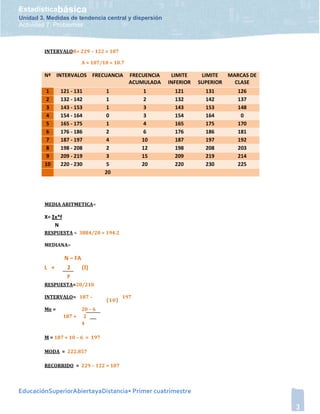
Este documento presenta un problema sobre medidas de tendencia central y dispersión para dos conjuntos de datos. El primer conjunto contiene tiempos de carrera de 20 estudiantes y se calculan las medidas utilizando frecuencias simples. El segundo conjunto contiene pesos de basura recolectados durante 20 días y se calculan las medidas usando intervalos de frecuencia.

1. Estadísticabásica
Unidad 3. Medidas de tendencia central y dispersión
Actividad 7: Problemas
Instrucción: Realiza lo siguiente para cada problema.
Elabora las tablas de frecuencias correspondientes para obtener las medidas de tendencia central y
dispersión.
Medias de tendencia central y dispersión por frecuencias simples, para el problema 1.
Medidas de tendencia central y dispersión por intervalos para el problema 2.
1. Un profesor de educación física desea hacer un estudio sobre el desempeño de sus alumnos(as) en
la prueba de atletismo de 100 metros planos. Seleccionó una muestra de 20 alumnos(as) y registró
los tiempos que éstos marcaron. Los tiempos, en segundos, registrados fueron:
18.71, 21.41, 20.72, 28.1, 19.29, 22.43, 20.17, 23.71, 19.44, 20.55, 18.92, 20.33, 23.00, 22.85, 19.25,
21.77, 22.11, 19.77, 18.04, 21.12.
MEDIA ARITMÉTICA
Como se trata de una muestra, para calcular la media utilizaremos la fórmula:
Como la frecuencia es la misma para todos los datos fi= 1 entonces la media será igual a la sumatoria
de todos los datos de i=1 hasta i=n entre el número total de datos n
Nº DATO FRECUENCIA FRECUENCIA FRECUANCIA
ACUMULADA ACUMULADA RELATIVA
1 18,04 1 0,0526 0,0526
2 18,71 1 0,0526 0,1052
3 18,92 1 0,0526 0,1578
4 19,25 1 0,0526 0,2104
5 19,29 1 0,0526 0,263
6 19,44 1 0,0526 0,0526
7 19,77 1 0,0526 0,3682
8 20,17 1 0,0526 0,4208
9 20,33 1 0,0526 0,4734
10 20,55 1 0,0526 0,526
11 20,72 1 0,0526 0,5786
12 21,12 1 0,0526 0,6312
13 21,41 1 0,0526 0,6838
14 21,77 1 0,0526 0,7364
15 22,11 1 0,0526 0,789
16 22,43 1 0,0526 0,8416
17 22,85 1 0,0526 0,8942
18 23,71 1 0,0526 0,9468
19 23 1 0,0526 0,9994
20 28,1 1 0,0526 1,052
1,052
EducaciónSuperiorAbiertayaDistancia• Primer cuatrimestre
1

2. Estadísticabásica
Unidad 3. Medidas de tendencia central y dispersión
Actividad 7: Problemas
2. Un ambientalista está haciendo una investigación sobre la cantidad de basura que se genera en
su colonia. Para ello registró cuántos kilos de basura recolectó el camión durante veinte días
consecutivos en su calle. Los resultados fueron:
227, 122, 172, 228, 217, 225, 182, 216, 229, 221, 192, 142, 152, 211, 192, 182, 203, 205, 187, 195.
X=Σx*f =
N
( 1 8 . 0 4 x 1 ) + ( 1 8 . 7 1 x 1 ) + ( 1 8 . 9 2 x 1 ) + ( 1 9 . 2 5 x 1 ) + ( 1 9 . 2 9 x 1 ) + ( 19.44x1) + (19.77x1)
+ ( 20.17x1) + ( 20.33x1) + (20.55x1) (+(20.72x1) +(21.12x1)+ (21.41) + (21.77) + (22.11) + (22.43) + (22.85x1) +
(23.00x1) + (23.71) + (28.1)
20
Total =421.69/20 = 21.08
MEDIA=20.55 + 20.72 = 41.27 / 2 = 20.635
MODA= En este caso no existe moda alguna ya que todas sus frecuencias equivalen a lo mismo.
RECORRIDO= Re = MAXi – MINi
Total= 28.1 – 18.04 = 10.06
VARIANZA= Su formula
(18.04 - 21.08)² +(18.71 -21.08)²+ (18.92-21.08)²+ (19.25-21.08)²+ (19.29-21.08)²+ (19.44-21.08)²+ (19.77-
21.08)²+ (20.17-21.08)²+ (20.33 - 21.08)²+(20.55-21.08)²+ (20.72-21.08)²+ (21.12-21.08)² + (21.41-21.08)²+
(21.77-21.08)²+ (22.11-21.08)²+ (22.43-21.08)²+ (22.85 - 21.08²)+ (23.00-21.08)²+(23.71-21.08)²+ (28.1-21.08)²
20
Continuando con la ecuación y reduciendo términos:
(-3.04)²+ (-2.37)²+ (-2.16)²+ (-1.83)²+ (-1.79)²+ (-1.64)²+ (-1.31)²+ (-0.91)²+(-0.75)²+ (-0.53)²+ (-0.36)²+ (-
0.04)² + (-0.33.)²+ (0.69)²+ (1.03)²+ (1.35)²+ (1.77)+ (1.92)²+ (2.63)²+ (7.02)²
20
9.24+5.61+4.66+3.34+3.20+2.68+1.71+0.82+1.73+0.56+0.28+0.12+0.0016+0.47+1.06+1.82+3.13+
3.68+6.91+49.28
20
TOTAL =100.30 = 5.015
20
VALOR DE LA DESVIACION =
EducaciónSuperiorAbiertayaDistancia• Primer cuatrimestre
2

3. Estadísticabásica
Unidad 3. Medidas de tendencia central y dispersión
Actividad 7: Problemas
INTERVALOR= 229 – 122 = 107
A = 107/10 = 10.7
Nº INTERVALOS FRECUANCIA FRECUENCIA LIMITE LIMITE MARCAS DE
ACUMULADA INFERIOR SUPERIOR CLASE
1 121 - 131 1 1 121 131 126
2 132 - 142 1 2 132 142 137
3 143 - 153 1 3 143 153 148
4 154 - 164 0 3 154 164 0
5 165 - 175 1 4 165 175 170
6 176 - 186 2 6 176 186 181
7 187 - 197 4 10 187 197 192
8 198 - 208 2 12 198 208 203
9 209 - 219 3 15 209 219 214
10 220 - 230 5 20 220 230 225
20
MEDIA ARITMETICA=
X= Σx*f
N
RESPUESTA = 3884/20 = 194.2
MEDIANA=
N – FA
L + 2 (I)
F
RESPUESTA=20/210
INTERVALO= 187 – 197
Me = 20 – 6
187 + 2
4
M = 187 + 10 – 6 = 197
MODA = 222.857
RECORRIDO = 229 – 122 = 107
EducaciónSuperiorAbiertayaDistancia• Primer cuatrimestre
3

4. Estadísticabásica
Unidad 3. Medidas de tendencia central y dispersión
Actividad 7: Problemas
VARIANZA =
Para calcular la varianza en este problema utilizaremos:
Donde es nuestra media aritmética = 194.2
Utilicemos una tabla para calcular los parámetros de la sumatoria de nuestra formula:
Nº INTERVALOS FRECUENCIAIA FRECUENCIA LIMITE LIMITE MARCAS MEDIA MC-µ (MC-µ)² (MC-µ)² * Fi
Fi ACUMULADA INFERIOR SUPERIOR DE CLASE ARITMETICA
1 121 - 131 1 1 121 131 126 192,2 -68,2 4651,24 4651,24
2 132 - 142 1 2 132 142 137 192,2 -57,2 3271,84 3271,84
3 143 - 153 1 3 143 153 148 192,2 -46,2 2134,44 2134,44
4 154 - 164 0 3 154 164 0 192,2 -35,2 1239,04 0,00
5 165 - 175 1 4 165 175 170 192,2 -24,2 585,64 585,64
6 176 - 186 2 6 176 186 181 192,2 -13,2 174,24 348,48
7 187 - 197 4 10 187 197 192 192,2 2,2 4,84 19,36
8 198 - 208 2 12 198 208 203 192,2 8,8 77,44 154,88
9 209 - 219 3 15 209 219 214 192,2 19,8 392,4 1176,12
10 220 - 230 5 20 220 230 225 192,2 30,8 948,2 4741,00
20 17083,00
VARIANZA = 17083 / 20 = 854.15
La desviación típica está dada por la raíz de la varianza:
DESVIACION TIPICA= √854.26 redondeado a decimales = 29.22
EducaciónSuperiorAbiertayaDistancia• Primer cuatrimestre
4