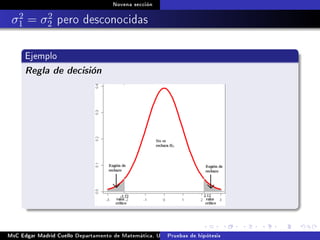
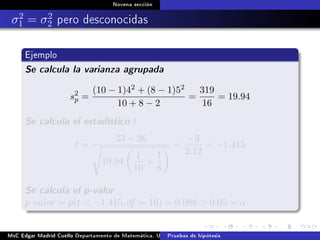
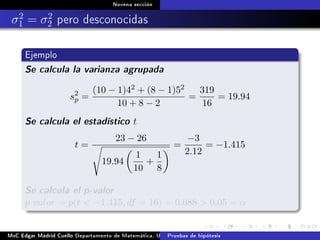
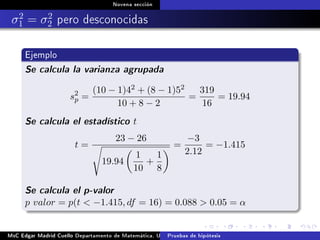
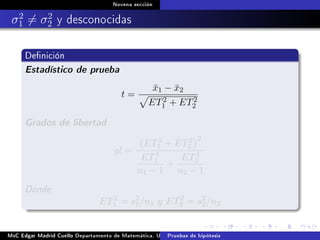
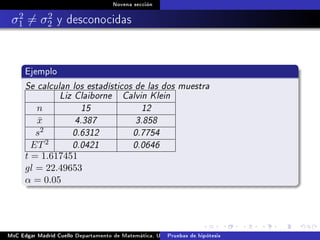
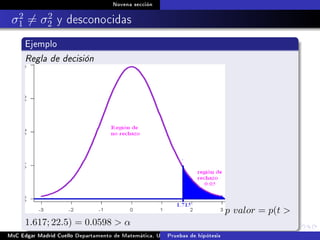
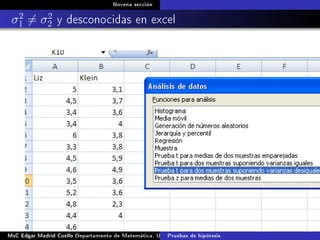
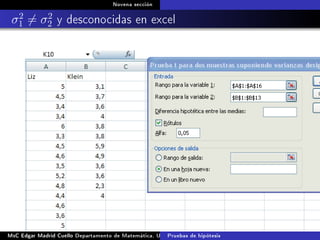
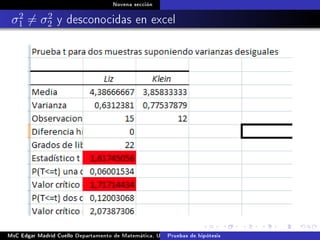
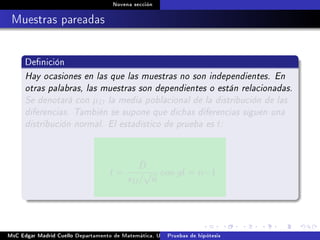
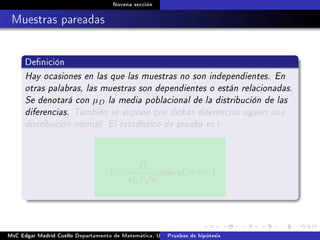
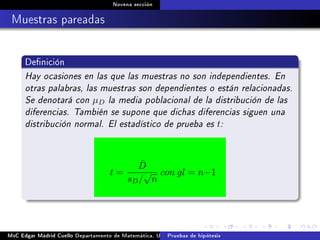
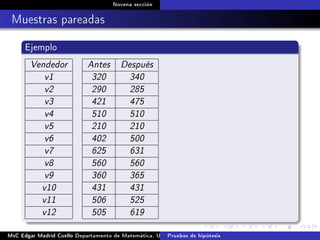
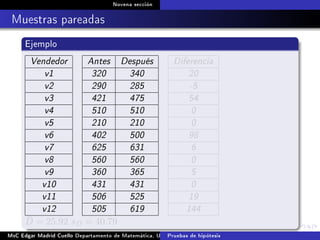
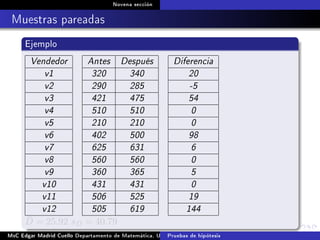
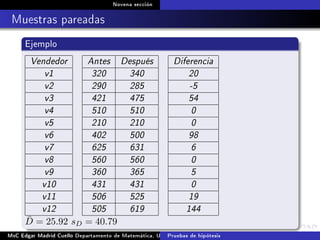
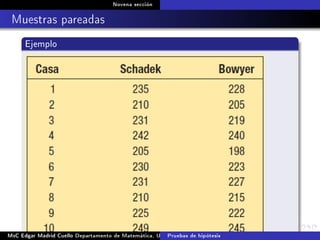
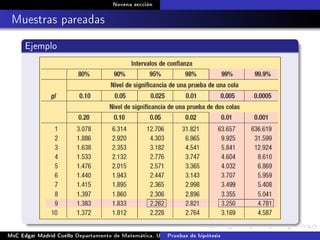
Este documento presenta los métodos para comparar medias poblacionales cuando las varianzas son desconocidas pero iguales. Explica cómo calcular la varianza agrupada, el estadístico t y el valor p para realizar una prueba t de student. También cubre ejemplos numéricos de comparación de medias usando este método y muestras pareadas.