Descargar para leer sin conexión
Subido porAndrew Aguillon
Ejercicio
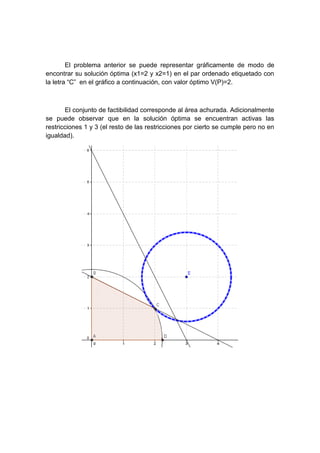
Este documento presenta un problema de programación no lineal con 2 variables de decisión y múltiples restricciones. Utiliza el Teorema de Karush-Kuhn-Tucker para encontrar la solución óptima, que involucra la activación de 2 restricciones. Verifica que la solución cumple las condiciones de primer y segundo orden, lo que demuestra que es un mínimo global y el problema es convexo.
Más contenido relacionado
La actualidad más candente
Ejercicio
- 1. EJERCICIO PROGRAMACION NO LINEAL. Integrante: AndrewAguillón CI: 22.998.456 Investigación de Operaciones II Porlamar, 22 de marzo de 2017
- 2. Las condiciones deoptimalidad establecidas en el Teorema de Karush Kuhn Tucker (KKT) permiten abordar la resolución de modelos de Programación No Lineal que consideran tanto restricciones de igualdad (ecuaciones) como desigualdad (inecuaciones). En términos comparativos las condiciones de KKT son más generales que el Método de Lagrange el cual se puede aplicar a problemas no lineales que consideran exclusivamente restricciones de igualdad. Mostraremos cómo utilizar el Teorema de Karush Kuhn Tucker para resolver un problema de Programación No Lineal con 2 variables de decisión. Sin pérdida de generalidad un modelo de Programación No Lineal se puede representar a través del siguiente formato: Luego podemos reescribir cualquier problema en dicha estructura manteniendo la equivalencia de la representación matemática. Para ejemplificar lo anterior consideremos el siguiente modelo de optimización no lineal que resulta de interés su resolución.
- 3. El problema anteriorse puede representar gráficamente de modo de encontrar su solución óptima (x1=2 y x2=1) en el par ordenado etiquetado con la letra “C” en el gráfico a continuación, con valor óptimo V(P)=2. El conjunto de factibilidad corresponde al área achurada. Adicionalmente se puede observar que en la solución óptima se encuentran activas las restricciones 1 y 3 (el resto de las restricciones por cierto se cumple pero no en igualdad).
- 4. Por supuesto laresolución mediante el Método Gráfico es sólo referencial y se ha utilizado en este caso para corroborar los resultados a obtener en la aplicación del teorema. En este contexto el problema en su forma estándar es simplemente: Notar que sólo fue necesario cambiar la forma de las restricciones de no negatividad (esto se puede hacer multiplicando por -1 cada una de ellas). Cabe destacar que en este caso en particular el problema no considera restricciones de igualdad. Luego las condiciones necesarias de primer orden de Karush Kuhn Tucker (KKT) están dadas por: Por ejemplo, si en las condiciones generales anteriores consideramos el problema no restringido (asumiendo que todas las restricciones son inactivas) la solución óptima por simple inspección es x1=3 y x2=2, que corresponde a la coordenada “E” de la gráfica anterior y que se puede observar no es una solución factible para el problema.
- 5. De este modola circunferencia de menor radio que intercepta el conjunto de factibilidad es precisamente aquella que pasa por la coordenada “C” donde las restricciones 1 y 3 se cumplen en igualdad, razón por la cual las cuales activaremos de forma simultanea: Al calcular los gradientes respectivos se obtiene: Lo cual da origen al siguiente sistema de ecuaciones: Reemplazando x1=2 y x2=1 podemos despejar los valores de los multiplicadores los cuales cumplen con las condiciones de no negatividad:
- 6. Adicionalmente se puedeverificar que x1=2 y x2=1 satisface las restricciones omitidas (2, 4 y 5) por lo cual se puede afirmar que dicha solución cumple las condiciones necesarias de primer orden de Karush Kuhn Tucker (KKT). A continuación verificamos el cumplimiento de las condiciones de segundo orden de KKT, en particular lo que tiene relación con la convexidad del problema. Para ello calculamos la Matriz Hessiana o de segundas derivadas de la función objetivo y las restricciones activas. El primer determinante de la Matriz Hessiana es D1=8/3>=0 y el segundo determinante es D2=(8/3)*(8/3)=(64/9)>=0. Se concluye que el problema es convexo y por tanto x1=2 y x2=1 es mínimo local y global para el problema. La resolución computacional de este problema con AMPL corrobora los resultados alcanzados:
- 7.