Este documento presenta un ejercicio de Matlab sobre el movimiento rectilíneo uniformemente variado (MRUV). El ejercicio implica medir el tiempo que tarda un móvil en recorrer diferentes distancias y graficar los datos para analizar la relación cuadrática entre el tiempo y la distancia. Se realiza un ajuste polinómico de segundo grado a los puntos de la gráfica y se grafica la función resultante para modelar el movimiento MRUV.

2. JUANITA COLES

3. ESTEBAN SANTACRUZ

5. Δr = área del trapecio Δr = semisuma de sus bases por la altura (2.2.4) (2.2.5) Si se despeja el tiempo (t) en la ecuación (2.2.3) y se reemplaza en la ecuación (2.2.4), se obtiene:

6. RELACION CUADRANTICA: MOVIMIENTO RECTILINEO UNIFORMEMENTE VARIADO 1.-Sobre el carro de pruebas ( cuya masa es 50 g) ubicar una masa de 150g , de manera que M=200g. 2.-Sobre el platillo para masas de ranura (cuya masas es de 1g) ubicar una masa de 2g, de manera que m=3g. 3.-Marcar sobre el carril, con un lápiz , las posiciones extremas donde puede estar el carro. Estas posiciones deben ser: a) aquella para la cual la masa m toca el piso. b) aquella que se encuentra a 80 cm de la posición descrita en (a) 4.-Dividir la distancia entre las posiciones extremas en 10 partes iguales. Marcar las divisiones sobre el carril con un lápiz. 5.-Desde cada una de las posiciones marcadas en le carril soltar el carro de pruebas ,desde el reposo. Tomar el tiempo que se demora en llegar a la posición extrema descrita en 3(a).Este tiempo debe ser tomado por 5 estudiantes con cronómetros. Anotar los valores en la tabla.

7. GRAFICAS Y FUNCIONESMOVIMIENTO RECTILINEO UNIFORMEMENTE VARIADO 1.- Medir el tiempo que se demora un móvil viajando con Movimiento Rectilíneo Uniformemente Variado (MRUV) al recorrer diferentes distancias. 2.-Con los datos obtenidos realizar una grafica de distancia vs. tiempo. 3.-Analizar la grafica obtenida.

8. Tabla del tiempo vs distancia

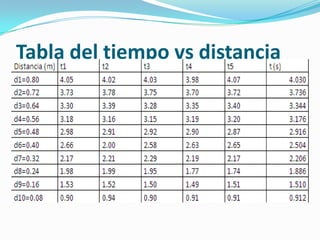
9. Datos del Ejercicio DISTANCIA >> d= [0.08 0.16 0.24 0.32 0.40 0.48 0.56 0.64 0.72 0.80] d = Columns 1 through 6 0.0800 0.1600 0.2400 0.3200 0.4000 0.4800 Columns 7 through 10 0.5600 0.6400 0.7200 0.8000 >> t=[0.91 1.51 1.89 2.21 2.50 2.92 3.18 3.35 3.74 4.03] t = Columns 1 through 6 0.9100 1.5100 1.8900 2.2100 2.5000 2.9200 Columns 7 through 10 3.1800 3.3500 3.7400 4.0300 >> plot(t,d,'o') Escribimos la distancia de la tabla de datos y procedemos a crear la variable (d), que implicara las distancias a recorrer. TIEMPO Procedemos a colocar cada uno de los tiempos promedio de cada fila, y establecemos la variable (t) para el tiempo.

10. Fórmulas del Ejercicio PLOT Genera una gráfica en las variables x e y, las mismas que en nuestra grafica serán tiempo(t)x y Distancia(d)y, y especificamos que se formarán circunferencias en donde estén los puntos >> plot (t,d,'o') >> polyfit(t,d,2) ans = 0.0241 0.1194 -0.0609 >> tg=1:0.01:4; >> f=0.0241*tg.^2+0.1194*tg-0.0609; >> holdon >> plot(tg,f) POLYFIT Es un comando que les permite a los puntos ajustarse según como vaya la curva de la parábola Holdon Hará que a partir de entonces todos los dibujos que se realicen aparezcan en la gráfica activa. Este comando sólo funciona para la gráfica que se ha ejecutado. ans Proviene del ingles answer y significa respuesta

11. Gráficas Movimiento rectilíneo uniformemente variado (d) distancia Movimiento rectilíneo uniformemente variado (d) (t) Tiempo distancia (t) Tiempo

12. Bibliografía http://www.monografias.com/trabajos37/movimiento-rectilineo/movimiento-rectilineo2.shtml http://ar.answers.yahoo.com/question/index?qid=20060714130450AAHhGR3 http://mygnet.net/codigos/matlab http://es.wikipedia.org/wiki/Movimiento_rectil%C3%ADneo_uniforme