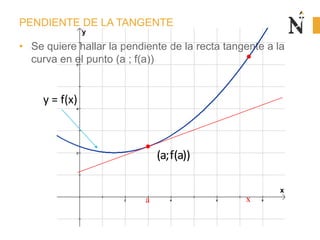
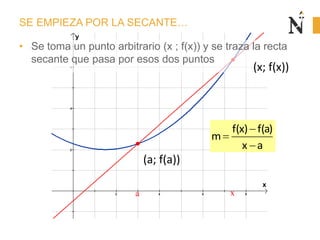
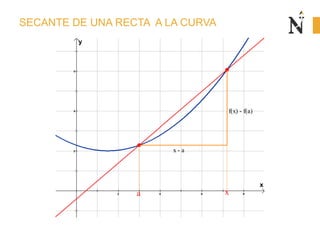
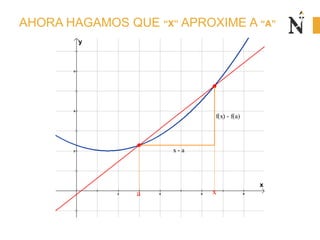
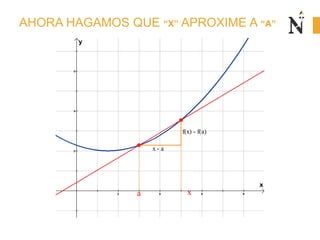
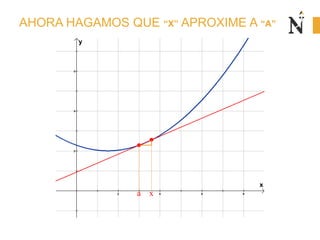
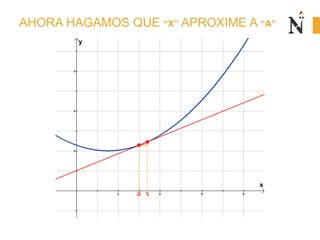
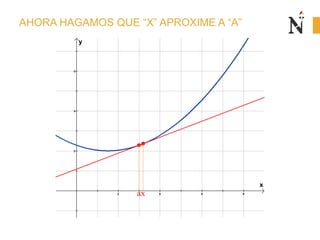
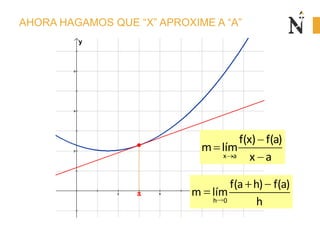
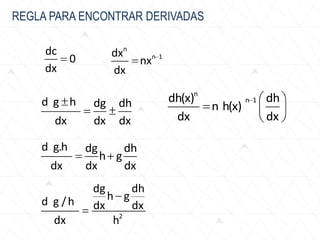
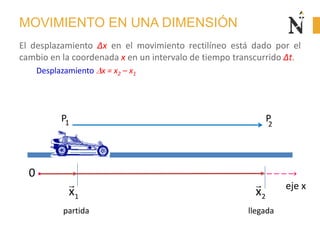
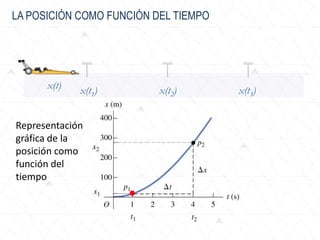
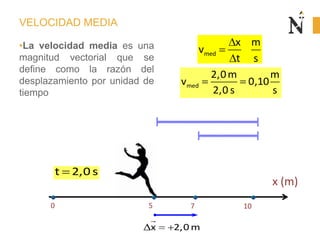
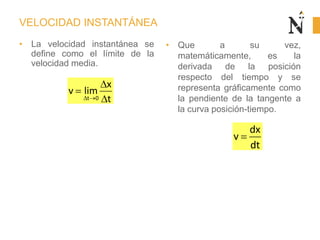
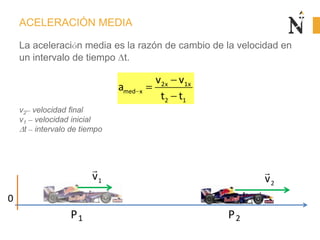
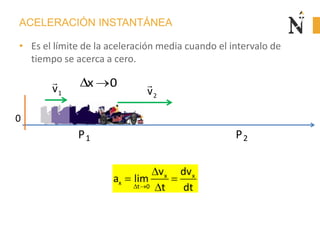
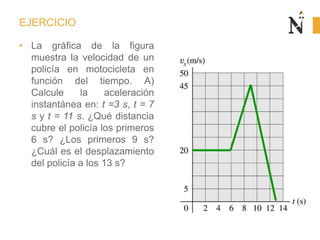
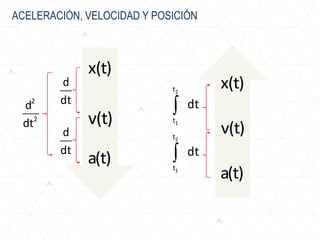
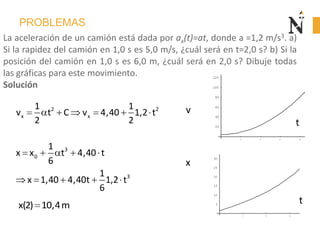
El documento trata sobre conceptos básicos de cinemática como velocidad media, velocidad instantánea, aceleración media y aceleración instantánea. Explica cómo calcular estas cantidades aplicando derivadas e integrales y define conceptos como MRU, MRUV. También incluye ejemplos numéricos y gráficos.

1. CINEMÁTICA
Repaso de derivadas e integrales de funciones polinómicas.
Velocidad media. Velocidad instantánea. Aceleración media.
Aceleración instantánea. MRU. MRUV.

2. LOGROS
• Al término de la sesión de aprendizaje el estudiante calcula la
velocidad y aceleración promedio así como la velocidad y
aceleración instantánea, aplicando la definición de razón de cambio
y reglas de derivación, con orden y seguridad mostrando una buena
presentación.

3. EL CINEMÓMETRO
Vea la infografía y responda si el cinemómetro mide
la velocidad instantánea de los vehículos

4. PENDIENTE DE LA TANGENTE
• Se quiere hallar la pendiente de la recta tangente a la
curva en el punto (a ; f(a))
2 4 6 8
2
4
6
x
y
a x
y = f(x)
(a;f(a))

5. 2 4 6 8
2
4
6
x
y
a x
SE EMPIEZA POR LA SECANTE…
• Se toma un punto arbitrario (x ; f(x)) y se traza la recta
secante que pasa por esos dos puntos
(a; f(a))
(x; f(x))
f(x) f(a)
m
x a

6. SECANTE DE UNA RECTA A LA CURVA
2 4 6 8
2
4
6
x
y
f(x) - f(a)
x - a
a x

7. AHORA HAGAMOS QUE “X” APROXIME A “A”
2 4 6 8
2
4
6
x
y
f(x) - f(a)
x - a
a x

8. AHORA HAGAMOS QUE “X” APROXIME A “A”
2 4 6 8
2
4
6
x
y
f(x) - f(a)
x - a
a x

9. AHORA HAGAMOS QUE “X” APROXIME A “A”
2 4 6 8
2
4
6
x
y
a x

10. AHORA HAGAMOS QUE “X” APROXIME A “A”
2 4 6 8
2
4
6
x
y
a x

11. AHORA HAGAMOS QUE “X” APROXIME A “A”
2 4 6 8
2
4
6
x
y
ax

12. AHORA HAGAMOS QUE “X” APROXIME A “A”
2 4 6 8
2
4
6
x
y
ax
x a
f(x) f(a)
m lím
x a
h 0
f(a h) f(a)
m lím
h

13. O EN SU FORMA EQUIVALENTE, H=X-A
• La derivada de una función f en un número a, denotada
con f’(a), es:
• Si el límite existe.
h 0
f(a h) f(a)
f'(a) lím
h

14. INTERPRETACIÓN GEOMÉTRICA
• La derivada de una función f(x) en un número a es la
pendiente de la recta tangente a la gráfica de la función
en el punto (a; f(a)).
• La derivada también se puede interpretar como la razón
de cambio de una magnitud respecto de otra.

15. REGLA PARA ENCONTRAR DERIVADAS
dc
0
dx
n
n 1dx
nx
dx
d g h dg dh
dx dx dx
d g.h dg dh
h g
dx dx dx
2
dg dh
h gd g /h dx dx
dx h
n
n 1dh(x) dh
n h(x)
dx dx

16. HALLAR LAS DERIVADAS
2
f(x) 5x 7x 6
Dadas las funciones:
6 5 2
f(x) 4x 3x 10x
2 2
f(x) (8x 5x)(13x 4)
2
4 x
f(x)
3 x
2
f(x) (5x 4)

17. LA CINEMÁTICA Y EL MOVIMIENTO
El estudio de la cinemática comienza con la definición de posición.
La posición es una magnitud vectorial que determina la ubicación de un
punto material en el eje coordenado.
1x

2x

La partícula pasa de la posición x1 a la posición x2
0
eje x

18. MOVIMIENTO EN UNA DIMENSIÓN
El desplazamiento Δx en el movimiento rectilíneo está dado por el
cambio en la coordenada x en un intervalo de tiempo transcurrido Δt.
Desplazamiento x = x2 – x1
1x

2x

0
eje x
P1 P2
partida llegada

19. LA POSICIÓN COMO FUNCIÓN DEL TIEMPO
x(t) x(t1) x(t2) x(t3)
Gráfica x-t
p1 p2
Representación
gráfica de la
posición como
función del
tiempo

20. VELOCIDAD MEDIA
•La velocidad media es una
magnitud vectorial que se
define como la razón del
desplazamiento por unidad de
tiempo
med
x m
v
t s
0 5 107
x 2,0 m

med
2,0m m
v 0,10
2,0 s s
t 2,0 s
x (m)

21. VELOCIDAD INSTANTÁNEA
• La velocidad instantánea se
define como el límite de la
velocidad media.
• Que a su vez,
matemáticamente, es la
derivada de la posición
respecto del tiempo y se
representa gráficamente como
la pendiente de la tangente a
la curva posición-tiempo.
t 0
x
v lim
t
dx
v
dt

22. EJERCICIO
• Un Honda Civic viaja en línea recta en carretera. Su distancia x de
un letrero de alto está dada en función de t por:
• Donde a =1,50 m/s2 y b=0,0500 m/s3.
• Calcule la velocidad media del auto para el intervalo de 0 a 2,00 s;
• Calcule la velocidad instantánea en t=0 y t=2,00 s.
2 3
x(t) t t

23. ACELERACIÓN MEDIA
La aceleración media es la razón de cambio de la velocidad en
un intervalo de tiempo t.
v2– velocidad final
v1 – velocidad inicial
t – intervalo de tiempo
2x 1x
med x
2 1
v v
a
t t
P1
1v

P2
2v

0

24. ACELERACIÓN INSTANTÁNEA
• Es el límite de la aceleración media cuando el intervalo de
tiempo se acerca a cero.
x x
x
t 0
v dv
a lim
t dt
P1
1v

P2
2v

0
x 0

25. EJERCICIO
• La gráfica de la figura
muestra la velocidad de un
policía en motocicleta en
función del tiempo. A)
Calcule la aceleración
instantánea en: t =3 s, t = 7
s y t = 11 s. ¿Qué distancia
cubre el policía los primeros
6 s? ¿Los primeros 9 s?
¿Cuál es el desplazamiento
del policía a los 13 s?

26. ACELERACIÓN, VELOCIDAD Y POSICIÓN
x(t)
v(t)
a(t)
x(t)
v(t)
a(t)
d
dt
d
dt
2
2
d
dt
2
1
t
t
dt
2
1
t
t
dt

27. PROBLEMAS
3
0
3
1
x x t 4,40 t
6
1
x 1,40 4,40t 1,2 t
6
La aceleración de un camión está dada por ax(t)=at, donde a =1,2 m/s3. a)
Si la rapidez del camión en 1,0 s es 5,0 m/s, ¿cuál será en t=2,0 s? b) Si la
posición del camión en 1,0 s es 6,0 m, ¿cuál será en 2,0 s? Dibuje todas
las gráficas para este movimiento.
Solución
1 2 3 4
5
10
15
20
25
30
x
t
2 2
x x
1 1
v t C v 4,40 1,2 t
2 2
x(2) 10,4m
2 4 6 8 10
20
40
60
80
100
120
v
t

28. MOVIMIENTO RECTILÍNEO UNIFORME
• Es aquel movimiento en el
que la velocidad del móvil
en cualquier instante
permanece constante.
• Es decir, el móvil se mueve
en línea recta, en una sola
dirección y con
desplazamientos iguales en
intervalos de tiempo
iguales.
• Debido a que la velocidad
no cambia, la aceleración
en este tipo de movimiento
es nula.
x
dx
v
dt
xx v dt
0 xx x v t

29. EJERCICIOS
• Ejercicio. Un vehículo parte de la posición -25,0 metros. Al cabo de
70,0 s se encuentra en la posición 245,0 metros. ¿Cuál ha sido el
valor de su velocidad si se sabe que realizó un MRU?
• Solución
• x1 = -25,0 m
• x2 = 245,0 m
• t = 70,0 s
245,0 ( 25,0)m
v
70,0 s
m
v 3,86
s

30. MOVIMIENTO CON ACELERACIÓN CONSTANTE
• En el movimiento rectilíneo
uniformemente variado se
cumple que la aceleración
es constante.
• Integrando la aceleración
se obtiene la expresión de
la velocidad.
• Antiderivando la velocidad
del paso anterior se obtiene
la expresión de la posición
instantánea del móvil.
0v v at
0x (v at)dt
2
0 0
1
x x v t at
2
0Si t 0, v v
0Si t 0, x x

31. CAÍDA LIBRE
g g j
•En el caso de la caída libre
(caída de un cuerpo cerca de la
superficie terrestre), se
considera que
g = 9,8 m/s2
•Eso significa que TODOS los
cuerpos, cerca de la superficie
terrestre, caen con la misma
aceleración.
0v v at
2
0
1
x x vt at
2
0v v gt
2
0
1
y y vt gt
2

32. EJERCICIOS
• Se deja caer un tabique (rapidez inicial cero) desde la
azotea de un edificio. El tabique choca con el piso 2,50 s
después. Se puede despreciar la resistencia del aire, así
que el tabique está en caída libre. a) ¿Qué altura tiene el
edificio? b) ¿Qué magnitud tiene la velocidad del tabique
justo antes de tocar el suelo? c) dibuje las gráficas ay-t,
vy-t y y-t para el movimiento.
2( 9,81)
0 H 0(2,50) (2,50)
2
y 2
o oy
a
y(t) y v t t
2
H 30,7m