Este documento describe un experimento para medir el desplazamiento de un carro en función del tiempo usando un cronómetro y una masa unida por un sedal. Se registraron los datos de distancia y tiempo para 10 puntos a lo largo de la pista. Usando MATLAB, los datos se graficaron y ajustaron a una curva parabólica para derivar la fórmula del desplazamiento.

1. Universidad Politécnica SalesianaIntegrantes: Roberth Valdivieso Wladimir Pachacama Edwin Acosta Johana Alminate Alejandro Herrera

2. TeoríaDeducción de la fórmula del desplazamiento

3. ExperimentoEn primer lugar señalamos la pista por donde a de pasar nuestro carro con un flexómetro en separaciones de 8 cmLuego amarramos una masa al extremo de un sedal y el otro extremo al carroUbicamos el carro en el primer punto señalado en la pista y dejamos que la masa y la fuerza de gravedad haga su funciónCon la ayuda de un cronometro tomamos el tiempo que se demora en llegar el carro desde el punto señalado hasta el extremo de la pistaY repetimos lo mismo para cada punto señalado en la pista anteriormenteDe esa manera obtenemos los datos para nuestro experimento.

4. Datos

5. Significados de cada fórmulaPlot(t,d,”o”)= Genera una grafica en las variables t siendo “o” un parámetro.Polyfit(t,d,”o”) = Es un comando que le permite ajustarse según como vaya la curva de la parábola . Ans= Es el resultado de las variables. f = Es una función .tg = Es el valor mínimo y valor máximo del tiempo.holdon = Mantiene el grafico anterior y el ultimo.plot(tg;f) = Genera una grafica en las variables tg y f.

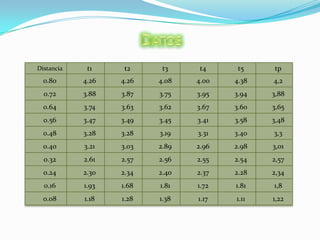
6. Ajuste en MATLAB1º Colocamos los datos de la distancia y del tiempo.>> d=[0.08 0.16 0.24 0.32 0.40 0.48 0.56 0.64 0.72 0.80]d = Columns 1 through 4 0.0800 0.1600 0.2400 0.3200 Columns 5 through 8 0.4000 0.4800 0.5600 0.6400 Columns 9 through 10 0.7200 0.8000>> t=[1.22 1.8 2.34 2.57 3.01 3.3 3.48 3.65 3.88 4.2]t = Columns 1 through 4 1.2200 1.8000 2.3400 2.5700 Columns 5 through 8 3.0100 3.3000 3.4800 3.6500 Columns 9 through 10 3.8800 4.2000

7. Una vez colocados los datos del tiempo y del desplazamiento salen los datos de las columnas y filas para una grafica. Para obtener el gráfico ponemos:>>plot(t,d,'o')>>polyfit(t,d,2)ans = 0.0513 -0.0296 0.0409>>tg=0.1: 0.001: 5;>> f=0.0513*tg.^2-0.0296*tg+0.0409;>> hold on>>plot(tg,f) Una vez hecho todo eso como gráfico resultante tenemos:

8. Graficos en MATLAB[m][s]

9. [m][s]